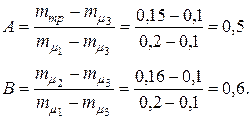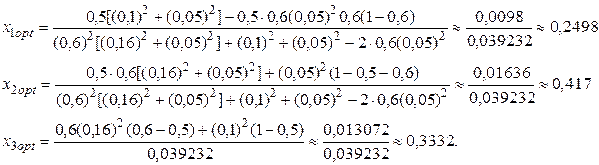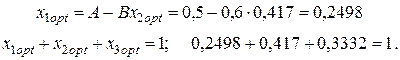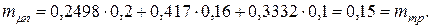Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Портфель минимального риска при заданной его эффективностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим портфель из двух видов бумаг, эффективность которых удовлетворяет условию
где значение Сделав замену переменной
При задании эффективности портфеля в виде равенства в (4.20)
В этом случае риск портфеля из двух видов бумаг однозначно определится формулой.
При задании эффективности портфеля в виде неравенства (4.20) структура портфеля минимального риска определяется наименьшим значением функции (4.23) на интервале значений х 1 заданных неравенством (4.21). Для нахождения наименьшего значения функции (4.21) на интервале (4.21) необходимо: 1) Приравнять производную функции (4.20) по х 1 нулю и из решения полученного уравнения определить значение 2) Если вычисленное значение
то это значение 3) Если вычисленное значение
Из формул (4.25) и условий
Пример 4.2. Определить стоимостные доли х 1 и х 2 портфеля ценных бумаг двух видов, обеспечивающие минимальный риск портфеля при заданной его эффективности Решение. Определим диапазон возможных значений стоимостной доли бумаг первого вида в соответствии с условием (4.20):
Так как по условию задачи
По формулам (4.25) определим значения
Вычислим значения
Для коэффициента корреляции
Из приведенных расчетов видно, что при
а минимальный риск портфеля ценных бумаг будет иметь значение:
При При
При
Таким образом, при Рассмотрим методику определения структуры портфеля ценных бумаг, состоящего из трех видов независимых бумаг, обеспечивающей минимальный риск портфеля при заданной его эффективности. Данную задачу можно представить в формализованном виде:
где выполняются соотношения:
Сделаем замену переменных
отсюда для
где После подстановки соотношений
Дифференцируя данное уравнение по х 2 и приравнивая производную нулю получим:
Отсюда для оптимального значения ценовой доли бумаг второго вида в портфеле из трех видов бумаг получим:
С учетом равенств
Структура портфеля, определяющаяся ценовыми долями бумаг Пример 4.3. Портфель состоит из трех видов независимых ценных бумаг, эффективность и риски которых имеют соответственно значения Определить структуру портфеля ценных бумаг Решение. По формулам (4.29) определим значение коэффициентов А и В:
По формулам (4.30) определяем оптимальные значения ценовых долей ценных бумаг первого, второго и третьего его вида:
Правильность вычисления значений
Вычислим эффективность портфеля ценных бумаг:
Вычислим риск портфеля ценных бумаг:
|
||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

 Требуемая эффективность такого портфеля может быть задана в виде:
Требуемая эффективность такого портфеля может быть задана в виде: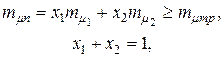 (4.20)
(4.20)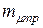 может быть задано в пределах
может быть задано в пределах 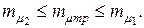
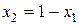 структуру портфеля, удовлетворяющую условию (4.20) можно определить в виде:
структуру портфеля, удовлетворяющую условию (4.20) можно определить в виде: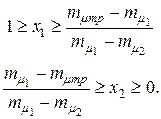 (4.21)
(4.21) Структура портфеля определена однозначно:
Структура портфеля определена однозначно: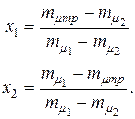 (4.22)
(4.22)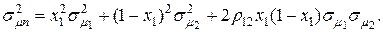 (4.23)
(4.23)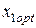 при котором обеспечивается минимум риска портфеля ценных бумаг
при котором обеспечивается минимум риска портфеля ценных бумаг 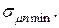
 (4.24)
(4.24)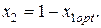
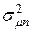 определяется формулой:
определяется формулой: (4.25)
(4.25)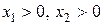 следует, что минимальное значение риска портфеля
следует, что минимальное значение риска портфеля 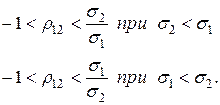 (4.26)
(4.26)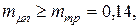 если эффективности и риски бумаг первого и второго вида соответственно равны
если эффективности и риски бумаг первого и второго вида соответственно равны 
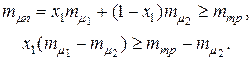
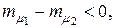 то для х 1 получим:
то для х 1 получим: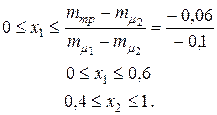 (4.27)
(4.27)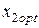 , обеспечивающие минимальный риск портфеля ценных бумаг при двух различных значениях коэффициента корреляции доходностей ценных бумаг. Из условий (4.26) следует, что при заданных рисков ценных бумаг оптимальные значения
, обеспечивающие минимальный риск портфеля ценных бумаг при двух различных значениях коэффициента корреляции доходностей ценных бумаг. Из условий (4.26) следует, что при заданных рисков ценных бумаг оптимальные значения 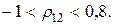
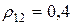 :
: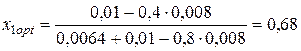
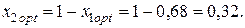
 оптимальная структура портфеля ценных бумаг двух видов определится значениями:
оптимальная структура портфеля ценных бумаг двух видов определится значениями: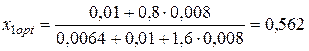


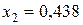 . При этих значениях эффективность портфеля бумаг будет равна:
. При этих значениях эффективность портфеля бумаг будет равна: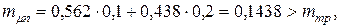
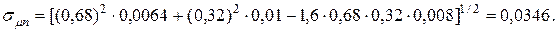
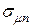 при его заданной эффективности определяется одной из границ интервала (4.27).
при его заданной эффективности определяется одной из границ интервала (4.27).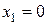 и
и 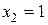 для значений
для значений 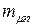 и
и 
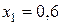 и
и 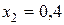 эффективность и риск портфеля ценных бумаг определяется значениями:
эффективность и риск портфеля ценных бумаг определяется значениями: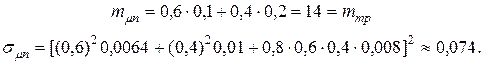
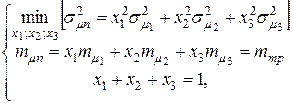 (4.28)
(4.28)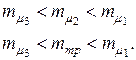
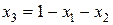 получим:
получим: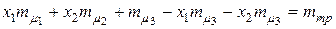
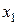 получим:
получим: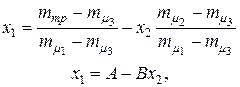 (4.29)
(4.29)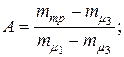
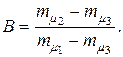
 в формулу (4.28) для риска портфеля ценных бумаг получим:
в формулу (4.28) для риска портфеля ценных бумаг получим: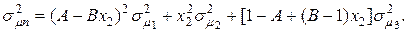
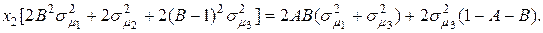
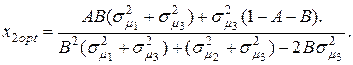 (4.30)
(4.30)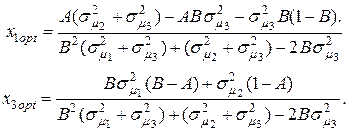 (4.30)
(4.30)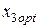 (формулы (4.30) обеспечивает минимум риска портфеля ценных бумаг при заданной его эффективности (4.28).
(формулы (4.30) обеспечивает минимум риска портфеля ценных бумаг при заданной его эффективности (4.28).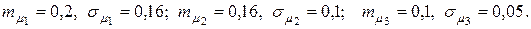
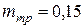 .
.