
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Институт финансов, экономики и менеджментаСодержание книги
Поиск на нашем сайте
Институт финансов, экономики и менеджмента А. М. Карлов АКТУАРНЫЕ РАСЧЕТЫ курс лекций для магистрантов по направлениям ______________- экономики и ______________ - менеджмент
Калининград Издательство ФГБОУ ВПО "КГТУ" ББК
УТВЕРЖДЕНО Ректором Калининградского государственного технического университета
Автор: А. М. Карлов, доктор технических наук, профессор кафедры ____________ Калининградского государственного технического университета.
Ó КГТУ, 2015. Ó Карлов А. М., 2015. Содержание
Тема 1. Теория процентов............................................................................................... 4 1.1. Доходность финансовой операции................................................................. 4 1.2. Простые проценты............................................................................................... 5 1.3. Сложные проценты.............................................................................................. 7 1.4. Дисконтирование и удержание процентов................................................... 9 1.5. Влияние инфляции на ставку процента...................................................... 12 1.6. Учет налогов при совершении финансовых операций........................... 17 1.7. Операции с валютой......................................................................................... 19
Тема 2. Финансовые потоки, ренты.......................................................................... 23 2.1. Основные понятия финансовых потоков.................................................... 23 2.2. Коэффициенты приведения и наращения рент........................................ 25 2.3. Срочные ренты................................................................................................... 28 2.4. Расчет r -срочной ренты при погашении кредита...................................... 31 2.5. Валютные кредиты............................................................................................ 35 2.6. Годовая и срочная ренты при m -кратном начислении процентов 39
Доходность финансовой операции
Под финансовой операцией понимают любые операции по вложению, размещению, инвестированию временно свободных денежных средств или их эквивалентов с целью получения дохода. Лицо, предоставляющее временно свободные средства является кредитором. Лицо, совершающее финансовые операции с этими средствами и берущее на себя обязательство вернуть через определенное время t эти средства, увеличенные на оговоренную сумму дохода, называют заемщиком. Обозначим первоначальную сумму размещаемых кредитором средств через S 0, а сумму возвращаемую заемщиком после совершения финансовой операции через
Доходность финансовой операции можно определить отношением:
Доходность финансовой операции оценивают в относительных величинах (1.1) или в процентах:
Сумма денежных средств, получаемая кредитором в конце финансовой операции, будет равна При принятии решения о вложении временно свободных денежных средств кредитор учитывает время t, через которое он получит их с доходом Естественно кредитор будет рассматривать несколько вариантов финансовых операций, среди которых будет практически безрисковое размещение денежных средств на банковский депозит с гарантированной годовой доходностью t = 1 год. Обозначим годовую доходность по банковским депозитным вкладам буквой i.
где Величину i называют годовой процентной ставкой – это сумма, выплачиваемая кредитору в конце периода начисления 1 год за каждую единичную сумму (например, Простые проценты Схема начисления простых процентов поясняется рис. 1.1.
Рис. 1.1. Схема начисления простых процентов Пусть первоначальная сумма, внесенная на депозит, равна
Если депозитный договор заключен на n -лет с фиксированной годовой процентной ставкой, при начислении дохода На текущем счете банковская процентная ставка равна нулю Если депозитный договор заключен на n -лет, то в конце срока вклада кредитор получит сумму:
При постоянной годовой процентной ставке
Если процентная ставка изменяется год от года, то:
где Если момент возврата ссуды является переменной величиной (например, депозитный вклад довостребования), то наращенная сумма в день выдачи ссуды определяется по формуле:
где
Если денежные средства в сумме
Иногда депозитные договора заключаются с m -кратным начислением процентов в году. При
где m - кратность начисления процентов в году; i – годовая процентная ставка. Тогда при сроке вклада 1 год проценты в размере
Отсюда следует, что при размещении средств по схеме простых процентов увеличение кратности выплат не приводит к увеличению наращенной суммы. В соответствии с формулой (1.4) наращенная сумма в схеме простых процентов является линейной возрастающей функцией с увеличением срока вклада (см. рис. 1.3).
Сложные проценты
Получение наращенной суммы
Рис. 1.2. Наращение суммы вклада по схеме сложных процентов
При наращении по схеме сложных процентов происходит реинвестирование, или капитализация полученных процентов. Предположим, денежные средства По истечении первого года наращенная сумма будет равна:
На втором году сумма депозитного вклада будет равна
К концу n -го года действия депозитного договора наращенная сумма будет определяться формулой:
Таким образом, последовательность наращенных сумм
где
Суммарный доход
Определим наращенную сумму при m -кратном начислении процентов в год. Если начисление сложных процентов происходит m -раз в году, то наращенная сумма при первом начислении процентов будет равна:
При втором начислении процентов:
По истечении одного года при m -том начислении процентов наращенная сумма будет равна:
Если депозитный договор с m -кратным начислением процентов и их капитализацией заключается на n- лет, то наращенную сумму можно определить по формуле:
Определим эффективную годовую процентную ставку
Отсюда для годовой эффективной процентной ставки получим:
Тогда формулу (1.10) для срока депозитного договора на n -лет при m -кратном начислении процентов можно записать в виде:
где В соответствии с формулами (1.6), (1.7) и (1.12) наращенная сумма в схеме сложных процентов является показательной функцией. Сравнение наращенных сумм вычисляемых по схеме простых и сложных процентов (см. рис. 1.3) позволяет сделать следующие выводы: 1) при сроке вклада один год наращение по схеме простых и сложных процентов при одинаковых процентных ставках имеют одинаковый коэффициент наращения; 2) при сроке вклада меньше одного года коэффициент наращения по схеме простых процентов больше чем при схеме сложных процентов; 3) при сроке вклада больше одного года коэффициент наращения по схеме сложных процентов больше чем при схеме простых процентов; 4) при наращении по схеме сложных процентов m -кратное начисление процентов приводит к увеличению коэффициента наращения; 5) при наращении по схеме простых процентов m -кратное начисление процентов не влияет на коэффициент наращения.
Рис. 1.3. Наращение по простой и сложной ставкам
Рис. 1.4. Дисконтирование по простой и сложной ставкам
3) Сумма, выплачиваемая клиенту при сроке n = 1 год до погашения денежного обязательства при его учете по простой и сложной схеме одинаковы. 4) При сроке учета t меньше одного года банку выгоднее учитывать денежное обязательство по сложной ставке дисконтирования, а при сроке учета больше года – по простой учетной ставке.
Рис. 1.5. Определение уровня инфляции за несколько периодов
После истечения двух периодов времени реальная стоимость первоначальной суммы денежных средств будет равна:
Для реальной стоимости денежных средств после истечения n периодов времени, по аналогии с формулой (1.22), можно записать:
Суммарный уровень инфляции за все n периодов должен давать такую же реальную стоимость денежных средств, как и формула (1.23):
Отсюда для суммарного уровня инфляции за n периодов получим:
Введем понятие среднего за период уровня инфляции. Если интервалы ti равны, например, одному месяцу; а n = 12, то будем говорить о среднегодовом уровне инфляции
Из этого равенства для среднегодового уровня инфляции получим формулу:
Оценим вначале влияние инфляции на годовую процентную ставку. При первоначальной сумме
где Формула (1.26) может быть преобразована к виду:
Из последнего равенства можно записать формулу для реально действующей в условиях инфляции годовой процентной ставки доходности
На рис. 1.6 приведены графики зависимости реальной готовой процентной ставки от суммарного годового уровня инфляции. Из приведенных графиков и формулы (1.27) видно, что реальная годовая процентная ставка доходности
Рис. 1.6. Зависимость реальной процентной ставки от уровня инфляции
Часто возникает обратная задача, определить под какую годовую процентную ставку i нужно разместить денежные средства, чтобы через год при заданном годовом уровне инфляции α Σ получить желаемое значение реально действующей, с учетом инфляции, процентной ставки ipα. При такой постановке в формуле (1.27) известными являются величины α Σ и ipα, а определить нужно i. В результате преобразований формулы (1.27) получим
1) Определим реально действующую процентную ставку с учетом инфляции при вложении денежных средств на депозитный договор сроком на n -месяцев при ежемесячном начислении процентов по схеме простых процентов. При начислении простых процентов наращенную сумму
По аналогии с формулой (1.27) можно получить реальную, действующую с учетом инфляции, доходность выше оговоренной финансовой операции по вложению суммы
где Поставим обратную задачу. Определим, при какой годовой процентной ставке по депозитному договору доходность данной финансовой операции будет не меньше чем
Из формулы (1.29) следует, что для получения реальной доходности 2) Определим реально действующую процентную ставку с учетом инфляции при вложении денежных средств Наращенную сумму
где
Определяя реальную доходность вложения денежных средств на депозит на n месяцев по схеме сложных процентов можно записать:
Определим, при какой годовой процентной ставке по депозитному договору на n месяцев при ежемесячном начислении процентов доходность данной финансовой операции с учетом инфляции будет не меньше чем
Определим значение i при
Операции с валютой
Возможность конвертации рублей в валюту и обратно валюты в рубли, а также возможность получения доходов от размещения на депозитах как рублевых, так и валютных вкладов увеличивают число возможных схем проведения данных финансовых операций. Предположим, что в наличии имеются временно свободные средства в российских рублях R, в долларах США $ и в евро?. Сравним доходы от размещения на депозите имеющихся денежных средств. Возможны следующие схемы получения дохода: · Без конвертации валюты 1) R → R 2) $ → $ 3)? →? · С конвертацией валюты 4) R → $ → $ → R 5) R →? →? → R 6) $ → R → R →$ 7)? → R → R →? 8) $ →? →? → $ 9)? → $ → $ →? Для сравнения доходности всех указанных схем финансовых операций введем следующие обозначения: PR – сумма депозитного вклада в рублях; P$ – сумма депозитного вклада в долларах США; P? – сумма депозитного вклада в евро; SR; S$; S? - наращенная за срок депозита сумма в рублях, долларах США и евро соответственно; K$R0; K$R1 – обменный курс долларов США в рубли в начале и в конце финансовой операции соответственно; K?R0; K?R1 – обменный курс евро в рубли в начале и в конце финансовой операции соответственно; K$?0; K$?1 – обменный курс долларов США в евро в начале и в конце финансовой операции соответственно; n – срок депозита; i – годовая процентная ставка по депозиту в рублях; j$ - годовая процентная ставка по депозиту в долларах США; j? - годовая процентная ставка по депозиту в евро. Получим формулы для оценки доходности финансовых операций для всех схем с конвертацией валюты. Для финансовых операций без конвертации валюты по схемам 1-3 формулы для определения наращенных сумм и множителей наращения приведены в п. 1.2 и 1.3 При наличии временно свободных средств во всех трех валютах PR; P$ и P? как средство снижения рисков потерь при изменении обменного курса валют рекомендуют их размещение на мультивалютном вкладе. Рассмотрим эту финансовую операцию на конкретном примере. Пример. В банке открыт мультивалютный вклад: 100 тыс. руб. под 13% годовых; 5 тыс. долл. США под 5% годовых и 10 тыс. евро под 4% годовых. Найти эффективную процентную ставку мультивалютного вклада, если курсы обмена валют в начале и в конце годового срока депозита равны 30 и 52; 40 и 62 руб. соответственно. Решение. Через год наращенные суммы будут равны: SR = PR (1 + i) = 100 тыс. руб. (1 + 0,13) = 113 тыс. руб. S $= P $(1 + j $) = 5000 (1 + 0,05) = 5250 $ S ?= P ?(1 + j ?) = 10000 (1 + 0,04) = 10400? Конвертируя первоначальные и наращенные суммы по курсам обмена валют на начало и окончание срока депозита получим: SR 0= 100000 + 5000 х 30 + 10000 х 40 = 650 тыс. руб. SR 1= 113000 + 5250 х 52 + 10400 х 62 = 1030,8 тыс. руб. Эффективная процентная ставка по мультивалютному вкладу с учетом изменения обменного курса валют определяется по формуле:
Откуда получим:
Если бы обменный курс валют не изменился, то наращенная сумма в рублях была бы равна:
а эффективная процентная ставка составила бы:
Если обменный курс валют не меняется, то эффективная процентная ставка равна средневзвешенному значению:
Последние шесть схем предполагают конвертацию валюты, как в начале, так и в конце финансовой операции. 4. Для наращенной суммы по четвертой схеме получим: - по депозитному договору с начислением простых процентов:
- по депозитному договору с начислением сложных процентов:
Множители наращения в схеме простых и сложных процентов можно записать в виде:
Из приведенных формул видно, что множитель наращения увеличивается с повышением годовой процентной ставки и с ростом обменного курса доллара к концу срока депозита. 5. Для пятой схемы совершения финансовой операции. Наращенные суммы по схеме простых и сложных процентов определяется формулами:
Множители наращения соответственно для простых и сложных процентов будут соответственно равны:
Из формул (1.39) видно, что (как и в схеме 4) множитель наращения увеличивается с повышением процентной ставки и с ростом обменного курса евро к концу срока депозитного договора. 6. Для шестой схемы финансовой операции. Наращенные суммы в долларах США при начислении простых и сложных процентов соответственно будут равны:
Для множителей наращения при начислении простых и сложных процентов получим формулы:
7. Для седьмой схемы финансовой операции. Наращенные суммы в евро при начислении простых и сложных процентов определяются формулами:
Для множителей наращения при начислении простых и сложных процентов будут равны:
Из формул (1.41) и (1.43) видно, что множители наращения в шестой и седьмой финансовых схемах увеличиваются с повышением процентной ставки по депозиту и с уменьшением обменного курса евро к рублю к окончанию срока депозита. 8. Для финансовой операции, реализуемой по восьмой схеме. Наращенные суммы в долларах США при начислении простых и сложных процентов можно определить по формулам:
где Множители наращения для данной финансовой операции определяются формулами:
Множители наращения финансовой операции по восьмой схеме увеличиваются при повышении процентной ставки и увеличении обменного курса 9. Для финансовой операции, реализуемой по девятой схеме. Наращенные суммы в евро при начислении простых и сложных процентов определяются формулам:
где Множители наращения в девятой схеме финансовой операции определяются формулами:
Как следует из формул (1.47) множители наращения увеличиваются при повышении процентных ставок и снижении обменного курса евро в долларах США к окончанию срока депозитного договора. Во всех схемах с конвертацией валюты наращенная сумма будет превышать первоначально вложенную сумму при M > 1. Из формул (1.47) следует, что множители ослабления будут больше единицы при соблюдении неравенств:
Аналогичные соотношения можно получить из формул (1.37), (1.39), (1.41), (1.43) и (1.45).
Основные понятия финансовых потоков
Финансовые потоки имеют широкое распространение на практике. Примерами финансовых потоков являются выплаты заработной платы, налоговые отчисления компании, коммунальные платежи, выплаты в погашение кредита, выплаты процентных доходов по депозитным договорам, ценным бумагам и т. п. Графическое представление финансового потока приведено на рис. 2.1.
Рис. 2.1. Графическое представление финансового потока
Платеж Р, произведенный в некоторый момент времени t называют финансовым событием. То есть финансовое событие – это упорядоченная пара значений (Р, t) определяющих размер платежа Р и дату (время) платежа t. Положительные платежи (со знаком плюс) означают поступление средств, отрицательные (со знаком минус) означают выплаты денежных средств. Финансовые потоки могут быть как конечной последовательностью финансовых событий, так и бесконечной. Финансовые потоки обозначаются символами CF (cash flow). Конечный финансовый поток, состоящий из (n + 1) финансовых событий, записывается в виде:
В общем случае платежи Как было показано в разделе 1, деньги должны работать и приносить доход. Денежные средства сегодня в размере
где Т – количество дней в году; i – годовая процентная ставка доходности. Текущее значение потока в момент времени t 0 называется современной величиной потока и обозначается просто
Для момента tn текущее значение потока называют конечным (накопленным) значением потока и обозначают
Среди финансовых потоков важное место занимают потоки платежей через равные промежутки времени. Эти потоки называют финансовой рентой или просто рентой. Промежуток времени между двумя соседними платежами называется периодом ренты. Если в финансовой ренте, состоящей из n платежей, первый платеж совершается в момент времени t 0, а n -ный платеж в момент времени tn – 1 (см. рис. 2.3), то такую ренту называют авансовой или пренумерандо. Если первый платеж совершается в момент времени t 1, а последний в момент времени tn (см. рис. 2.2), то такая рента называется обыкновенной, подрасчетной или постнумерандо. Промежуток времени между началом первого периода t 0 и окончанием последнего периода tn называется сроком ренты. Если все платежи равны между собой Ренты описываются следующими параметрами: размером отдельного платежа, периодом и сроком ренты, процентной ставкой i, числом платежей в году r (r – срочные ренты), а также методом начисления процентов – простые и сложные, а также частотой m начисления процентов в году (m – кратные ренты). В случае, когда период ренты равен одному году, такую ренту называют годовой или аннуитетом (annuity). В русскоязычной финансовой литературе аннуитетом называют постоянную ренту с произвольным периодом.
Рента постнумерандо Финансовый поток постоянной ренты постнумерандо можно записать в виде:
где R – размер платежей. Графическое представление постоянной годовой ренты постнумерандо приведено на рис. 2.2.
Рис. 2.2. Конечная годовая постоянная рента постнумерандо
Найдем современную стоимость ренты
В правой части равенства (2.4) имеем сумму членов убывающей геометрической прогрессии со знаменателем
С учетом значений а 1 и q для современной стоимости ренты постнумерандо получим:
Множитель при R называют коэффициентом приведения ренты и обозначают
Наращенная конечная сумма ренты обозначается
Данная сумма является суммой n -членов возрастающей геометрической прогрессии со знаменателем
Множитель при R называют коэффициентом наращения и обозначают
Из сравнения формул (2.7) и (2.9) следует:
Коэффициенты приведения Из формулы (2.10) можно записать соотношение между конечной S и современной А стоимостью ренты постнумерандо:
Рента пренумерандо Финансовый поток годовой постоянной ренты пренумерандо можно записать в виде:
Графическое представление ренты пренумерандо приведено на рис. 2.3.
Рис. 2.3. Конечная годовая постоянная рента пренумерандо
Найдем современную стоимость ренты пренумерандо | |||||||
|
| Поделиться: |

 где
где  - величина дохода, полученного от использования первоначальной суммы в течение времени t.
- величина дохода, полученного от использования первоначальной суммы в течение времени t. (1.1)
(1.1)
 где
где  - доходность в относительных единицах.
- доходность в относительных единицах.
 и
и  - величина дохода, и общая сумма получаемая кредитором после истечения одного года вклада.
- величина дохода, и общая сумма получаемая кредитором после истечения одного года вклада. тыс. руб.) занятую заемщиком в начале периода.
тыс. руб.) занятую заемщиком в начале периода.
 при годовой процентной ставке i. Тогда наращенная за год сумма будет равна:
при годовой процентной ставке i. Тогда наращенная за год сумма будет равна:
 по схеме простых процентов, то в конце каждого года этот доход переводится на текущий счет, а сумма, размещенная на депозите, остается постоянной равной
по схеме простых процентов, то в конце каждого года этот доход переводится на текущий счет, а сумма, размещенная на депозите, остается постоянной равной  Доходы, перечисляемые на текущий счет, могут по усмотрению кредитора или оставаться на текущем счете или изыматься для своих нужд.
Доходы, перечисляемые на текущий счет, могут по усмотрению кредитора или оставаться на текущем счете или изыматься для своих нужд.
 и конечная наращенная за n -лет сумма будет равна:
и конечная наращенная за n -лет сумма будет равна: (1.2)
(1.2) (1.3)
(1.3) - годовая процентная ставка в k -том году.
- годовая процентная ставка в k -том году. (1.4)
(1.4) - день вложения средств на депозит;
- день вложения средств на депозит; - день возврата средств;
- день возврата средств; - срок действия депозитного договора в днях;
- срок действия депозитного договора в днях; - количество дней в году.
- количество дней в году. дней с разными годовыми процентными ставками
дней с разными годовыми процентными ставками 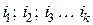 , то наращенная сумма
, то наращенная сумма  за весь период времени
за весь период времени  будет равна:
будет равна: (1.5)
(1.5)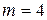 , проценты начисляются и могут быть выплачены ежеквартально, при
, проценты начисляются и могут быть выплачены ежеквартально, при  - ежемесячно. В этом случае наращенная сумма на первом сроке выплаты процентов будет равна:
- ежемесячно. В этом случае наращенная сумма на первом сроке выплаты процентов будет равна:
 будут начислены m раз, и наращенная сумма по истечения года будет равна:
будут начислены m раз, и наращенная сумма по истечения года будет равна:
 при начислении процентов по схеме сложных процентов поясняется рис. 1.2.
при начислении процентов по схеме сложных процентов поясняется рис. 1.2.

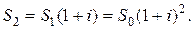
 (1.6)
(1.6) является геометрической прогрессией с начальным членом
является геометрической прогрессией с начальным членом  Коэффициент пропорциональности
Коэффициент пропорциональности  между наращенной
между наращенной  (1.7)
(1.7) - количество дней в году.
- количество дней в году.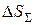 , получаемый за весь срок депозитного вклада в соответствии с формулами (1.6) и (1.7) может быть представлен в виде:
, получаемый за весь срок депозитного вклада в соответствии с формулами (1.6) и (1.7) может быть представлен в виде: (1.8)
(1.8)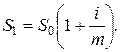

 (1.9)
(1.9)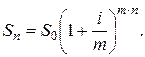 (1.10)
(1.10) при m -кратном начислении процентов с их капитализацией из равенства получаемых за год наращенных сумм:
при m -кратном начислении процентов с их капитализацией из равенства получаемых за год наращенных сумм:
 (1.11)
(1.11) (1.12)
(1.12)
 (1.22)
(1.22) (1.23)
(1.23)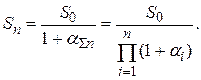
 (1.24)
(1.24) . При таком подходе можно считать уровень инфляции во всех месяцах года постоянным; равным среднегодовому
. При таком подходе можно считать уровень инфляции во всех месяцах года постоянным; равным среднегодовому  . С учетом данного равенства формулу (1.23) можно записать в виде:
. С учетом данного равенства формулу (1.23) можно записать в виде:
 (1.25)
(1.25) наращенная сумма
наращенная сумма  через один год с учетом инфляции может быть определена по формуле:
через один год с учетом инфляции может быть определена по формуле: (1.26)
(1.26) - суммарный годовой уровень инфляции, определяемый по формуле (1.24) по данным о ежемесячном уровне инфляции
- суммарный годовой уровень инфляции, определяемый по формуле (1.24) по данным о ежемесячном уровне инфляции  .
.

 (1.27)
(1.27) . При
. При 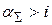 несмотря на вложение денежных средств с обещанной доходностью i % фактически первоначальная вложенная сумма
несмотря на вложение денежных средств с обещанной доходностью i % фактически первоначальная вложенная сумма 

 с учетом данных о ежемесячной инфляции
с учетом данных о ежемесячной инфляции  можно определить по формуле:
можно определить по формуле:
 (1.28)
(1.28) - суммарный уровень инфляции за n месяцев депозитного договора.
- суммарный уровень инфляции за n месяцев депозитного договора. . Из формулы (1.28) получим:
. Из формулы (1.28) получим: (1.29)
(1.29) при вложении денежных средств на депозитный договор на срок 12 месяцев при суммарной годовой инфляции
при вложении денежных средств на депозитный договор на срок 12 месяцев при суммарной годовой инфляции  годовая процентная ставка по депозиту должна быть не меньше 18,8%.
годовая процентная ставка по депозиту должна быть не меньше 18,8%.
 - средний за период n месяцев уровень ежемесячной инфляции определяемой по формуле (1.25).
- средний за период n месяцев уровень ежемесячной инфляции определяемой по формуле (1.25).
 (1.30)
(1.30) (1.31)
(1.31) . Тогда при вложении денежных средств на депозит на 12 месяцев с ежемесячным начислением процентов по схеме сложных процентов годовая процентная ставка по депозиту должна быть не меньше 17,5%.
. Тогда при вложении денежных средств на депозит на 12 месяцев с ежемесячным начислением процентов по схеме сложных процентов годовая процентная ставка по депозиту должна быть не меньше 17,5%.

 тыс. руб.,
тыс. руб.,

 (1.35)
(1.35) (1.36)
(1.36) (1.37)
(1.37) (1.38)
(1.38) (1.39)
(1.39) (1.40)
(1.40) (1.41)
(1.41) (1.42)
(1.42) (1.43)
(1.43) (1.44)
(1.44) - обменный курс долларов США в евро может быть рассчитан по формуле
- обменный курс долларов США в евро может быть рассчитан по формуле  .
. (1.45)
(1.45) к концу срока депозита.
к концу срока депозита. (1.46)
(1.46) - обменный курс покупки доллар США за евро, который может быть рассчитан по формуле
- обменный курс покупки доллар США за евро, который может быть рассчитан по формуле  .
. (1.47)
(1.47)


 могут быть различными по величине, интервалы времени между соседними платежами
могут быть различными по величине, интервалы времени между соседними платежами 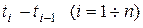 и доходность
и доходность  финансовых операций на этих интервалах также могут принимать различные значения.
финансовых операций на этих интервалах также могут принимать различные значения. через время
через время  с учетом возможного дохода могут иметь стоимость
с учетом возможного дохода могут иметь стоимость  Поэтому непосредственно суммировать размеры платежей
Поэтому непосредственно суммировать размеры платежей  совершаемые в разное время не корректно. Для того чтобы вычислить величину потока в какой-то момент времени
совершаемые в разное время не корректно. Для того чтобы вычислить величину потока в какой-то момент времени  необходимо пересчитать все платежи от
необходимо пересчитать все платежи от  до
до  с учетом их наращенной стоимости, а все платежи
с учетом их наращенной стоимости, а все платежи 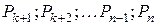 дисконтировать к моменту времени
дисконтировать к моменту времени  . Сумма всех платежей финансового потока, приведенных к некоторому моменту времени
. Сумма всех платежей финансового потока, приведенных к некоторому моменту времени  При начислении дохода по сложной процентной ставке i % годовых для
При начислении дохода по сложной процентной ставке i % годовых для  можно записать:
можно записать: (2.1)
(2.1) - количество календарных дней с момента t 0 до tk;
- количество календарных дней с момента t 0 до tk; без индекса:
без индекса: (2.2)
(2.2)
 (2.3)
(2.3) то такую ренту называют постоянной.
то такую ренту называют постоянной.

 постнумерандо. В соответствии с формулой (2.2) получим:
постнумерандо. В соответствии с формулой (2.2) получим: (2.4)
(2.4) и первым членом
и первым членом  Сумма n -членов геометрической прогрессии определяется формулой:
Сумма n -членов геометрической прогрессии определяется формулой: (2.5)
(2.5) (2.6)
(2.6)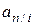 :
: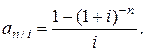 (2.7)
(2.7) и определяется суммой (2.3):
и определяется суммой (2.3):
 и первым членом R. В соответствии с формулой (2.5) получим:
и первым членом R. В соответствии с формулой (2.5) получим: (2.8)
(2.8) :
: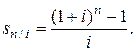 (2.9)
(2.9) (2.10)
(2.10)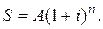 (2.11)
(2.11)




