
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учет налогов при совершении финансовых операцийСодержание книги
Поиск на нашем сайте
Рассмотрим методику учета налогов при определении эффективной процентной ставки по банковским вкладам на депозит и при получении банковских кредитов. 1) Учет налогов по депозитным договорам Проценты по вкладам в коммерческом банке не облагаются налогами, если они не превышают ставку рефинансирования Центрального Банка России, увеличенную на 5 %. Обозначим это пороговое значение Рассчитаем эффективную процентную ставку для данного случая. Наращенную величину вклада по истечении года можно определить по формуле:
Отсюда для эффективной процентной ставки при наличии налоговых отчислений
Пример. Вклад помещен в банк под семнадцать процентов годовых Решение. Определяем ставку отсечения
По формуле (1.32) вычисляем эффективную процентную ставку при ставке налога
Таким образом, реальная эффективная процентная ставка с учетом уплаченных налогов будет равна 15,6%, т. е. на 1,4% ниже объявленной банком процентной ставки по вкладу.
2) Учет налогов по кредитным договорам Проценты за кредит исключаются из налогооблагаемой базы налога на прибыль организации, если они не превышают ставку отсечения Для рублевых кредитов Определим эффективную процентную ставку по кредиту, если процентная ставка, указанная в кредитном договоре i не превышает ставку отсечения
где D – сумма кредита. Отсюда для эффективной процентной ставки получим:
Величину Если процентная ставка по кредиту i, указанная в кредитном договоре, превышает ставку отсечения
Приравнивая данное выражение значению
При Пример. Кредит взят под 20% годовых. Найти эффективную кредитную процентную ставку, если ставка отсечения равна Решение. Так как
Таким образом, реально выплаченная эффективная процентная ставка по кредиту равна 18,24%, т. е. на 1,76% меньше процентной ставки, указанной в кредитном договоре.
Операции с валютой
Возможность конвертации рублей в валюту и обратно валюты в рубли, а также возможность получения доходов от размещения на депозитах как рублевых, так и валютных вкладов увеличивают число возможных схем проведения данных финансовых операций. Предположим, что в наличии имеются временно свободные средства в российских рублях R, в долларах США $ и в евро?. Сравним доходы от размещения на депозите имеющихся денежных средств. Возможны следующие схемы получения дохода: · Без конвертации валюты 1) R → R 2) $ → $ 3)? →? · С конвертацией валюты 4) R → $ → $ → R 5) R →? →? → R 6) $ → R → R →$ 7)? → R → R →? 8) $ →? →? → $ 9)? → $ → $ →? Для сравнения доходности всех указанных схем финансовых операций введем следующие обозначения: PR – сумма депозитного вклада в рублях; P$ – сумма депозитного вклада в долларах США; P? – сумма депозитного вклада в евро; SR; S$; S? - наращенная за срок депозита сумма в рублях, долларах США и евро соответственно; K$R0; K$R1 – обменный курс долларов США в рубли в начале и в конце финансовой операции соответственно; K?R0; K?R1 – обменный курс евро в рубли в начале и в конце финансовой операции соответственно; K$?0; K$?1 – обменный курс долларов США в евро в начале и в конце финансовой операции соответственно; n – срок депозита; i – годовая процентная ставка по депозиту в рублях; j$ - годовая процентная ставка по депозиту в долларах США; j? - годовая процентная ставка по депозиту в евро. Получим формулы для оценки доходности финансовых операций для всех схем с конвертацией валюты. Для финансовых операций без конвертации валюты по схемам 1-3 формулы для определения наращенных сумм и множителей наращения приведены в п. 1.2 и 1.3
При наличии временно свободных средств во всех трех валютах PR; P$ и P? как средство снижения рисков потерь при изменении обменного курса валют рекомендуют их размещение на мультивалютном вкладе. Рассмотрим эту финансовую операцию на конкретном примере. Пример. В банке открыт мультивалютный вклад: 100 тыс. руб. под 13% годовых; 5 тыс. долл. США под 5% годовых и 10 тыс. евро под 4% годовых. Найти эффективную процентную ставку мультивалютного вклада, если курсы обмена валют в начале и в конце годового срока депозита равны 30 и 52; 40 и 62 руб. соответственно. Решение. Через год наращенные суммы будут равны: SR = PR (1 + i) = 100 тыс. руб. (1 + 0,13) = 113 тыс. руб. S $= P $(1 + j $) = 5000 (1 + 0,05) = 5250 $ S ?= P ?(1 + j ?) = 10000 (1 + 0,04) = 10400? Конвертируя первоначальные и наращенные суммы по курсам обмена валют на начало и окончание срока депозита получим: SR 0= 100000 + 5000 х 30 + 10000 х 40 = 650 тыс. руб. SR 1= 113000 + 5250 х 52 + 10400 х 62 = 1030,8 тыс. руб. Эффективная процентная ставка по мультивалютному вкладу с учетом изменения обменного курса валют определяется по формуле:
Откуда получим:
Если бы обменный курс валют не изменился, то наращенная сумма в рублях была бы равна:
а эффективная процентная ставка составила бы:
Если обменный курс валют не меняется, то эффективная процентная ставка равна средневзвешенному значению:
Последние шесть схем предполагают конвертацию валюты, как в начале, так и в конце финансовой операции. 4. Для наращенной суммы по четвертой схеме получим: - по депозитному договору с начислением простых процентов:
- по депозитному договору с начислением сложных процентов:
Множители наращения в схеме простых и сложных процентов можно записать в виде:
Из приведенных формул видно, что множитель наращения увеличивается с повышением годовой процентной ставки и с ростом обменного курса доллара к концу срока депозита. 5. Для пятой схемы совершения финансовой операции. Наращенные суммы по схеме простых и сложных процентов определяется формулами:
Множители наращения соответственно для простых и сложных процентов будут соответственно равны:
Из формул (1.39) видно, что (как и в схеме 4) множитель наращения увеличивается с повышением процентной ставки и с ростом обменного курса евро к концу срока депозитного договора. 6. Для шестой схемы финансовой операции. Наращенные суммы в долларах США при начислении простых и сложных процентов соответственно будут равны:
Для множителей наращения при начислении простых и сложных процентов получим формулы:
7. Для седьмой схемы финансовой операции. Наращенные суммы в евро при начислении простых и сложных процентов определяются формулами:
Для множителей наращения при начислении простых и сложных процентов будут равны:
Из формул (1.41) и (1.43) видно, что множители наращения в шестой и седьмой финансовых схемах увеличиваются с повышением процентной ставки по депозиту и с уменьшением обменного курса евро к рублю к окончанию срока депозита. 8. Для финансовой операции, реализуемой по восьмой схеме. Наращенные суммы в долларах США при начислении простых и сложных процентов можно определить по формулам:
где
Множители наращения для данной финансовой операции определяются формулами:
Множители наращения финансовой операции по восьмой схеме увеличиваются при повышении процентной ставки и увеличении обменного курса 9. Для финансовой операции, реализуемой по девятой схеме. Наращенные суммы в евро при начислении простых и сложных процентов определяются формулам:
где Множители наращения в девятой схеме финансовой операции определяются формулами:
Как следует из формул (1.47) множители наращения увеличиваются при повышении процентных ставок и снижении обменного курса евро в долларах США к окончанию срока депозитного договора. Во всех схемах с конвертацией валюты наращенная сумма будет превышать первоначально вложенную сумму при M > 1. Из формул (1.47) следует, что множители ослабления будут больше единицы при соблюдении неравенств:
Аналогичные соотношения можно получить из формул (1.37), (1.39), (1.41), (1.43) и (1.45).
|
|||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.194.29 (0.011 с.) |

 . В противном случае при
. В противном случае при  с суммы доходов по процентам превышающих ставку
с суммы доходов по процентам превышающих ставку  , взимается налог
, взимается налог  .
.
 получим:
получим: (1.32)
(1.32) . Найти эффективную процентную ставку по вкладу при ставке рефинансирования Банка России
. Найти эффективную процентную ставку по вкладу при ставке рефинансирования Банка России  .
. .
.
 - по валютным кредитам.
- по валютным кредитам. Банка России на несколько процентных пунктов.
Банка России на несколько процентных пунктов. . В этом случае платежи в счет погашения кредита, выплачиваемые из чистой прибыли (после уплаты налога на прибыль) можно определить по формуле:
. В этом случае платежи в счет погашения кредита, выплачиваемые из чистой прибыли (после уплаты налога на прибыль) можно определить по формуле:
 (1.33)
(1.33) называют налоговым щитом. Она показывает финансовую выгоду компании при использовании заемного капитала.
называют налоговым щитом. Она показывает финансовую выгоду компании при использовании заемного капитала. . С учетом этого для эффективной процентной ставки получим:
. С учетом этого для эффективной процентной ставки получим:
 для эффективной процентной ставки по кредиту ставки по кредиту получим:
для эффективной процентной ставки по кредиту ставки по кредиту получим: (1.34)
(1.34) в формуле (1.34) должна быть взята равной нулю и формула (1.34) совпадает с формулой (1.33).
в формуле (1.34) должна быть взята равной нулю и формула (1.34) совпадает с формулой (1.33). а ставка налога на прибыль равна
а ставка налога на прибыль равна  .
. рассчитываем по формуле (1.34):
рассчитываем по формуле (1.34):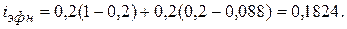


 тыс. руб.,
тыс. руб.,

 (1.35)
(1.35) (1.36)
(1.36) (1.37)
(1.37) (1.38)
(1.38) (1.39)
(1.39) (1.40)
(1.40) (1.41)
(1.41) (1.42)
(1.42) (1.43)
(1.43) (1.44)
(1.44) - обменный курс долларов США в евро может быть рассчитан по формуле
- обменный курс долларов США в евро может быть рассчитан по формуле  .
. (1.45)
(1.45) к концу срока депозита.
к концу срока депозита. (1.46)
(1.46) - обменный курс покупки доллар США за евро, который может быть рассчитан по формуле
- обменный курс покупки доллар США за евро, который может быть рассчитан по формуле  .
. (1.47)
(1.47)



