
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи об оптимальном портфеле.Содержание книги
Поиск на нашем сайте
В литературе [1, 7, 8, 9] описаны подходы к формированию оптимального портфеля с помощью моделей Блека, Марковица, Тобина. Задача оптимизации заключается в том, чтобы определить, какая доля портфеля должна быть отведена для каждой из инвестиций так, чтобы величина ожидаемого дохода и уровень риска соответствовали целям инвесторов. Например, целевой функцией может быть минимизация риска при заданной доходности, или максимизация дохода при риске не выше заданного. При этом на компоненты вектора Х, представляющего портфель, могут накладываться различные ограничения, зависящие от вида сделки, типа участвующих активов, величины открываемых позиций и т. д. Портфели, удовлетворяющие условиям данного рынка называются допустимыми. 1) В модели Блека допустимыми являются любые портфели. Это значит, что вектор Х удовлетворяет лишь основному ограничению:
Наличие коротких позиций (отсутствие условия неотрицательности) позволяет реализовать любую, сколь угодно большую доходность, естественно за счет большого риска. 2) В модели Марковица допустимыми являются только стандартные портфели (без коротких позиций). Это значит, что на вектор Х накладываются два ограничения: основное и неотрицательности xi ³ 0 для всех i. Портфель называют стандартным, если инвестор по каждому активу находится в длинной (long) позиции. Длинная позиция — это обычно покупка актива с намерением его последующей продажи (закрытие позиций). Такая покупка обычно осуществляется при ожидании повышения цены актива в надежде получить доход от разности цен покупки и продажи. Допустим, что относительно некоторого актива инвестор уверен в обратном, то есть в понижении его стоимости. В этом случае он может совершить сделку, которая называется короткой продажей (short sale). Для этого он берет данный актив взаймы у другого инвестора (кредитора), сразу же продает его, а впоследствии покупает на рынке по сниженной цене и возвращает его своему кредитору. При этом он обязан выплатить кредитору текущий доход по активу за время сделки и некоторый процент за предоставление самой возможности сделки (за кредит). На большинстве фондовых бирж короткие продажи вполне допустимы и часто используются, но ввиду их особой рискованности биржи могут вводить ограничения на общую величину коротких позиций в сделках.
Особенностью модели Марковица является то, что доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен. 3) Модель Тобина-Шарпа-Литнера. В этой модели предполагается наличие так назывемых безрисковых активов, доходность которых не зависит от состояния рынка и имеет постоянное значение. Пример 4..1. Сформировать портфель минимального риска из двух видов ценных бумаг - АРТ с эффективностью12% и риском 21.1 и ВЕРМ с эффективностью 5.1% и риском 8.3 при условии, что обеспечивается доходность портфеля (mp =S xi mi) не менее 8.9%. Коэффициент корреляции равен 0.18. Решение. Модель Марковица может быть сформулирована следующим образом. Необходимо найти вектор Х= (X1, X2), минимизирующий риск портфеля sp. X1 - доля в портфеле ценных бумаг АРТ; X2 - доля в портфеле ценных бумаг ВЕРМ, sp= = При ограничениях: X1 + X2 =1 12´X1 + 5.1´X2 ³ 8.9 X1,X2 ³ 0
Графический метод решения задачи дает следующие результаты.
Довольно легко можно получить решение задачи в среде EXCEL с помощью надстройки Поиск решения. (Рис.4.4. и табл. 4.2.).
Рис.4.4. В ячейке Е5 получено минимальное значение целевой функции.
Табл. 4.2.Фрагмент отчета по результатам.
Ответ: Минимальный риск портфеля равный 12.88% будет достигнут, если доля акций АРТ составит 0.55, а доля акций ВЕРМ – 0.45. Пример 4.2. Найти оптимальный портфель максимальной эффективности для трех ценных бумаг REXX, SNS и LIKX с доходностью и риском:
Матрица коэффициентов корреляции
Верхняя граница риска задана равной 16. Решение. Модель может быть сформулирована следующим образом.
Необходимо найти вектор Х= (X1, X2 , X3), максимизирующий доходность портфеля mp. X1 – доля в портфеле ценных бумаг REXX, X2 – доля в портфеле ценных бумаг SNS, X3 – доля в портфеле ценных бумаг LIKX. mp=12´X1+7´X2+11´X3®max при ограничениях X1 + X2 + X3 =1 sp= X1,X2, X3 ³ 0
Матрица ковариаций получена с использованием формулы[iv] COVi,j= ri,j ´ si ´ s j,. COV= Для решения задачи следует воспользоваться надстройкой EXCEL Поиск решения [10]. В результате решения получена максимально возможная доходность портфеля 11.29 при значениях вектора Х, записанных в ячейки $G1:$I1 (Рис. 4.5.)
Рис. 4.5. Фрагмент листа ЕХСЕL с исходными данными и результатами (X).
Ответ: Максимальную доходность 11.324% можно получить, если доли акций REXX, SNS и LIKX составят 0.47, 0.29 и 0.25
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.181.206 (0.009 с.) |


 =
=  =
=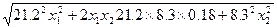 ® min
® min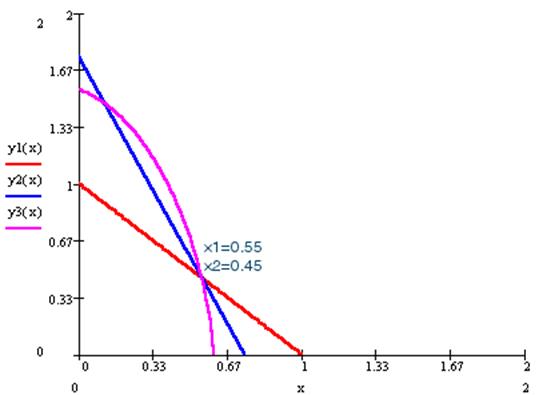

 16
16





