
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ общего риска: активы, рассматриваемые изолированноСодержание книги
Поиск на нашем сайте
Понятия распределения вероятностей и ожидаемой величины могут использоваться как основа для измерения риска. Известно, что риск присутствует в том случае, если исследуемые распределения имеют более одного возможного исхода, однако каким образом можно измерить риск и оценить его количественно? Чтобы ответить на этот вопрос, рассмотрим сначала методику исчисления общего риска. Выше мы предположили, что возможны 5 состояний экономики (см. табл. 3.1). На самом же деле состояние экономики может варьироваться от самой глубокой депрессии до наивысшего подъема с бесчисленным количеством промежуточных положений. Обычно среднему (нормальному) состоянию соответствует самая большая вероятность, далее значения вероятностей равномерно уменьшаются при удалении от нормы как в одну (подъем), так и в другую (спад) сторону, стремясь к нулю в крайних положениях (полная депрессия и наибольший подъем). Если при этом величина доходности, соответствующая нормальному положению, является одновременно и средним арифметическим двух крайних значений, то мы получаем распределение, которое в теории вероятностей носит название «нормального». Его графическое изображение дано на рис. 3.2. Нормальное распределение достаточно полно отражает реальную ситуацию и дает возможность, используя ограниченную информацию, получать числовые характеристики, необходимые для оценки степени риска того или иного проекта. Далее будем всегда предполагать, что мы находимся в условиях нормального распределения вероятностей. Замечание. В действительности в чистом виде нормальное распределение в экономических явлениях встречается редко, однако, если однородность совокупности соблюдена, часто фактические распределения близки к нормальному.
Вопрос 2. Реальные распределения вероятностей могут существенно отличаться от нормального. Насколько сильно будут искажены наши выводы, если в наших рассуждениях мы будем исходить только из нормального закона распределения вероятностей? Ответ: а) затрудняюсь ответить; б) существенно искажены; в) искажения будут несущественными. Правильный ответ в). При любом варианте ответа см. справку 2.
Справка 2. Даже если распределение не является близким к нормальному, на основании теоремы Чебышева можно утверждать, что для любого распределения не менее 89% всех исходов лежит в пределах трех средних квадратических отклонений от ожидаемого значения.
ERR Рис. 3.2. Нормальное распределение вероятностей
На рисунке 3.1 приведены графики распределения вероятностей для проектов 1 и 2. Условиям нормального распределения удовлетворяет проект 2. Для большей прозрачности дальнейших рассуждений, полезно предварительно решить самостоятельно следующую задачу
Задача 1. Рассмотрим два финансовых проекта А и В, для которых возможные нормы доходности (IRR) находятся в зависимости от будущего состояния экономики. Данная зависимость отражена в таблице 3.2 Таблица 3.2. Данные для расчета ожидаемой нормы доходности вариантов вложения капитала в проекты А и В
Рассчитайте для каждого из проектов ожидаемую норму доходности ERR. Сравните результаты своих вычислений с ответом. Ответ: Для проекта А по формуле (3.1) получаем: ERRА = 0,25 ´ 90% + 0,5 ´ 20% + 0,25 ´ (-50%) = 20%. Для проекта В: ERRВ = 0,25 ´ 25% + 0,5 ´ 20% + 0,25 ´ 15% = 20%
Таким образом, для двух рассматриваемых проектов ожидаемые нормы доходности совпадают, несмотря на то, что диапазон возможных значений IRR сильно различается: у проекта А от -50% до 90%, у проекта В от 15% до 25%. На рисунке 3.3 приведены графики распределения вероятностей для проектов А и В, (они удовлетворяют условиям нормального распределения).
Рис. 3.3. Распределение вероятностей для проектов А и В Предполагается, что для проекта А в наихудшем случае убыток не составит более 50%, а в наилучшем случае доход не превысит 90%. Для проекта В 15% и 25% соответственно. Очевидно, что тогда значение ERR останется прежним (20%) для обоих проектов, совпадая со значением среднего состояния. Соответствующая же среднему значению вероятность понизится, причем не одинаково в наших двух случаях.
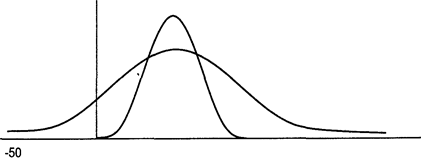
Рис. 3.4. Распределение вероятностей для проектов А и В Очевидно, чем более «сжат» график, тем выше вероятность, соответствующая среднему ожидаемому доходу (ERR), и вероятность того, что величина реальной доходности окажется достаточно близкой к ERR. Тем ниже будет и риск, связанный с соответствующим проектом. Поэтому меру «сжатости» графика можно принять за достаточно корректную меру риска. Меру «сжатости» определяет величина, которая в теории вероятности носит название «среднеквадратичного отклонения» - s - и рассчитывается по следующей формуле
Чем меньше величина s, тем больше «сжато» соответствующее распределение вероятностей, и тем менее рискован проект. При этом для нормального распределения вероятность «попадания» в пределы ERR ± s составляет 68,26%. Рассчитаем значение s для рассматриваемых проектов А и В. Проект А:
Проект В:
Как видим, для второго проекта с вероятностью 68,26% можно ожидать величину доходности IRR = 20% ± 3,5%, т.е. от 16,5% до 23,5%. Риск здесь минимальный. Проект А гораздо более рискованный. С вероятностью 68,26% можно получить доходность от -29,5% до 69,5%. Считается, что среднерискованной операции соответствует значение s около 30%. В рассмотренном примере распределение вероятностей предполагалось известным заранее. Во многих ситуациях бывают доступны лишь данные о том, какой доход приносила некая финансовая или хозяйственная операция в предыдущие годы. С позиции развиваемых представлений проанализируем рассмотренный в самом начале темы пример 1. Рассчитаем, например, дисперсию доходности проекта 2 по данным табл. 3.1. Нам известно, что ожидаемая доходность проекта, равна 12.0%. Следовательно, дисперсия равна
+(15,0-12,0)20,20 + (26,0-12,0)20,05 = 23,20, а среднее квадратическое отклонение доходности проекта 2 – s = 4,82% Используя этот показатель в качестве меры разброса, можно сделать ряд полезных выводов о распределении исходов. В частности, если распределение является непрерывным и близким к нормальному, можно утверждать, что 68.3% всех исходов лежит в пределах одного среднего квадратического отклонения от ожидаемого значения, 95.4% — в пределах двух средних квадратических отклонений и практически все исходы (99.7%) — в пределах трех средних квадратических отклонений. В табл. 3.3 приводятся ожидаемые значения доходности, дисперсия и среднее квадратическое отклонение по всем четырем альтернативным вариантам инвестирования примера 1, а также коэффициент вариации, который мы рассмотрим в следующем разделе. Мы видим, что ГКО-ОФЗ обладают наименьшими значениями показателей дисперсии и среднего квадратического отклонения, а проекту 2 соответствуют наибольшие их значения. По данным табл. 3.3 можно, казалось бы, прийти к заключению, что казначейские векселя — наименее рисковый вариант инвестирования, а проект 2 — наиболее рисковый. Однако это не всегда верно; перед тем как сделать окончательный вывод, необходимо принять во внимание ряд других факторов, таких как численные значения ожидаемой доходности, асимметрия распределения, достоверность наших оценок распределения вероятностей и взаимосвязь каждого актива с другими активами, включенными в портфель инвестиций.
Таблица 3.3 Оценка доходности и риска четырех альтернативных вариантов инвестирования
Вопрос 3. Достаточно ли отчетливо Вы представляете себе, как учитывать асимметрию распределения вероятностей? Если «да», изучайте материал далее, если «нет» – обратитесь к справке 3.
Спрака 3. Анализируя риск, логично сосредоточиться в основном на вероятностях тех значений доходности, которые меньше ожидаемого значения, а не на тех, которые его превышают. Если распределение является симметричным, и дисперсия и среднее квадратическое отклонение будут точно измерять риск получения доходности ниже ожидаемого значения, который составляет ровно половину общего риска. Однако если распределение асимметрично, эти показатели неверно отражают действительный риск. Если распределение обладает правосторонней асимметрией, дисперсия и среднее квадратическое отклонение завышают риск получения доходности ниже ожидаемого значения, а если распределение имеет левостороннюю асимметрию, наблюдается противоположная ситуация. Статистической характеристикой, элиминирующей эти искажения, является полудисперсия (semivariance, SV), которая определяется по формуле
SV = (8,0 – 9,2)0,52 + (8,5 – 9,2)20,20 + (9,0 – 9,2)20,50 = 0,19. Показатели полудисперсии четырех вариантов инвестирования, перечисленных в табл. 2.1, имеют следующие значения: 0,00; 0,19; 12,54 и 11,60. Если распределение симметрично, то полудисперсия составляет половину дисперсии. Это верно для проекта 2. Однако полудисперсия проекта 1 составляет более половины дисперсии — поскольку распределение доходности проекта 1 имеет левостороннюю асимметрию, его дисперсия занижает риск получения доходности ниже ожидаемого значения. Полудисперсия корпоративных ценных бумаг меньше половины дисперсии — поскольку распределение доходности имеет правостороннюю асимметрию, его дисперсия завышает риск получения доходности ниже ожидаемого значения. Финансовая статистика, как правило, недостаточно точна, чтобы применять к ней высокоточные аналитические методы, а большинство распределений, которые мы рассматриваем, близко к симметричным, поэтому мы остановимся на дисперсии и среднем квадратическом отклонении как мерах разброса.
Коэффициент вариации Еще одной величиной, характеризующей степень риска, является коэффициент вариации CV. Он рассчитывается по следующей формуле: CV = s/ERR (3.4) и выражает количество риска на единицу доходности. Естественно, чем выше CV, тем выше степень риска.
Упражнение 2. Рассчитать коэффициенты вариации для проектов А и В задачи 1, используя ранее полученные среднеквадратические отклонения sА = 49,5% и sВ = 3,5%. Сравните Ваши результаты с ответом. Ответ: CVA = 49,5/20 = 2,475; CVB = 3,5/20 = 0,175.
Коэффициенты вариации для проектов А и В задачи 1, рассчитанные в упражнении 2, в данной ситуации уже не добавляют существенной информации и могут служить лишь для оценки того, во сколько раз один проект рискованнее другого: 2,475/ 0,175 = 14. Проект А в 14 раз рискованнее проекта В. Коэффициент вариации необходимо знать в случае, когда требуется сравнить финансовые операции с различными ожидаемыми нормами доходности ERR. Пример 2. Пусть для проектов С и D распределение вероятностей задается следующей таблицей 3.4: Таблица 3.4. Распределение вероятностей для проектов С и D
Упражнение 3. Рассчитайте для обоих проектов ERR, s и CV. Рассчитанные значения сравните с данными приведенными в тексте.
По формуле (3.1) получаем: ERRC = 30´0,2 + 20´0,6 + 10´0,2 = 20%; ERRD= 115´0,2 + 80´0,6 + 45´0,2 = 80%. По формуле (3,2):
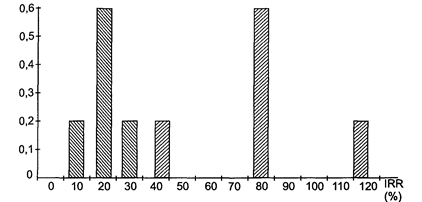
Таким образом, у проекта D величина s намного больше, но при этом больше и значение ERR. Для того чтобы можно было принять решение в пользу того или иного проекта, необходимо рассчитать коэффициент CV, отражающий соотношение между ERR и s (см. также рис. 3.5).
Рис 3.5. Распределение вероятностей для проектов C и D По формуле (3.4) найдем: CVС = 6,3/20 = 0,315; CVD = 22,14/80 = 0,276. Как видно, несмотря на достаточно большое значение s, величина CV для проекта D меньше, т.е. меньше риска на единицу доходности, что достигается за счет достаточно большой величины ERRD. В данном случае расчет коэффициента CV дает возможность принять решение в пользу второго проекта.
Упражнение 4. Рассчитайте коэффициенты вариации для четырех исходных вариантов инвестирования примера 1. Какой из проектов – 1 или 2 – окажется наименее рискованным? В рассуждениях опирайтесь на все уже известные Вам измерители риска. Сравните свои выводы с ответом. Ответ: В 4-й строке табл. 3.2 приведены значения коэффициентов вариации для четырех исходных вариантов инвестирования. Как следует из данных таблицы, классификация проектов по коэффициенту вариации как мере риска отличается от классификации, основанной на измерении риска с помощью ожидаемой нормы доходности: проект 2 является более рисковым, чем проект 1, по критерию среднего квадратического отклонения, а после корректировки различий в доходности и измерения риска с помощью коэффициента вариации вывод будет прямо противоположным.
Итак, мы получили два параметра, позволяющие количественно определить степень возможного риска: среднеквадратичное отклонение s и коэффициент вариации CV. Но при этом мы вынуждены отметить, что определение степени риска не всегда позволяет однозначно принять решение в пользу того или иного проекта. В этой вязи необходимо рассмотреть следующий пример. Пример 3. Известно, что вложение капитала в проекты К и L в последние четыре года приносило следующий доход (см. табл. 3.5). Выяснить, в какой из проектов вложение капитала связано с меньшим риском. Таблица 3.5 Доходность проектов К и L в динамике
Решение. В примерах 1-2 и задаче 1 распределение вероятностей предполагалось известным заранее. Во многих ситуациях доступны лишь данные о том, какой доход приносила некая финансовая или хозяйственная операция в предыдущие годы. Именно такой характер имеет доступная информация в примере 3. В подобных случаях для расчета среднеквадратичного отклонения s используется такая формула
Здесь n — число лет, за которые приведены данные, a ARR (ARR — Average Rate of Return, средняя норма доходности)— среднее арифметическое всех IRR за n лет — рассчитывается по формуле:
Таким образом, по формуле (3.6) рассчитаем среднюю норму доходности для обоих проектов: ARRK = (20 + 15 + 18 + 3)/4 = 19%; ARRL = (40 + 24 + 30 + 50)/4 = 36%. По формуле (3.5) найдем величину среднеквадратичного отклонения
Видим, что у проекта L средняя норма доходности выше, но при этом выше и величина s. Поэтому необходимо рассчитать коэффициент вариации CV. По формуле (3.4) получаем: CVK = 2,9/19= 0,15; CVL = 9,9 / 36 = 0,275. Коэффициент вариации для проекта L выше почти в 2 раза, следовательно, вложение в этот проект почти вдвое рискованнее . Однако данные таблицы 3.5 говорят, что минимальная доходность проекта L выше максимальной доходности проекта К. Очевидно, что вложение в проект L в любом случае более рентабельно. Полученные же значения s и CV означают не возможность получения более низкой доходности, а возможность неполучения ожидаемой доходности от проекта L.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.193 (0.008 с.) |






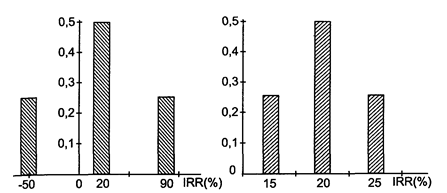
 (3.2)
(3.2) %
% %
% = (-2,0 – 12,0)20,05 + (9,0 – 12,0)20,20 + (12,0-12,0)20,50 +
= (-2,0 – 12,0)20,05 + (9,0 – 12,0)20,20 + (12,0-12,0)20,50 +




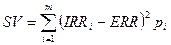 , (3.3)
, (3.3) где т — множество исходов, которые лежат ниже ожидаемого значения. Рассмотрим, например, возможность покупки корпоративных ценных бумаг (табл. 3.1). Учитывая, что их ожидаемая доходность составляет 9.2%, рассчитаем полудисперсию в соответствии с формулой (3.3)
где т — множество исходов, которые лежат ниже ожидаемого значения. Рассмотрим, например, возможность покупки корпоративных ценных бумаг (табл. 3.1). Учитывая, что их ожидаемая доходность составляет 9.2%, рассчитаем полудисперсию в соответствии с формулой (3.3)







 (3.5)
(3.5) (3.6)
(3.6)




