
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальность по Парето двухкритериальных финансовыхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Операций в условиях неопределенности Из рассмотренного выше следует, что каждое решение (финансовая операция) имеет две характеристики, которые нуждаются в оптимизации: средний ожидаемый доход и средний ожидаемый риск. Таким образом, выбор наилучшего решения является оптимизационной двухкритериальной задачей. В задачах многокритериальной оптимизации основным понятием является понятие оптимальности по Парето [6]. Рассмотрим это понятие для финансовых операций с двумя указанными характеристиками. Пусть каждая операция а имеет две числовые характеристики Е(а), r(а) (например, эффективность и риск); при оптимизации Е стремятся увеличить, а r уменьшить. Существует несколько способов постановки таких оптимизационных задач. Рассмотрим такую задачу в общем виде. Пусть А — некоторое множество операций, и разные операции обязательно различаются хотя бы одной характеристикой. При выборе наилучшей операции желательно, чтобы Е было больше, а r меньше. Будем говорить, что операция а доминирует операцию b, и обозначать а > b, если Е(а) ≥ Е(b) и r(a) ≤ r(b) и хотя бы одно из этих неравенств строгое. При этом операция а называется доминирующей, а операция b – доминируемой. Очевидно, что никакая доминируемая операция не может быть признана наилучшей. Следовательно, наилучшую операцию надо искать среди недоминируемых операций. Множество недоминируемых операций называется множеством (областью) Парето или множеством оптимальности по Парето [7]. Для множества Парето справедливо утверждение: каждая из характеристик Е, r является однозначной функцией другой, т.е. на множестве Парето по одной характеристике операции можно однозначно определить другую. Вернемся к анализу финансовых решений в условиях частичной неопределенности. Как показано в разделе 2.3, каждая операция характеризуется средним ожидаемым риском Для определения лучшей операции в ряде случаев можно применять некоторую взвешивающую формулу, в которую характеристики Пример 2.9. Пусть исходные данные те же, что и в примерах 2.6 и 2.7, т.е. для матриц последствий и риска примера 2.1 известны вероятности вариантов развития реальной ситуации: p1 =1/2, p2=1/6, p3=1/6, p4=1/6. В этих условиях ЛПР согласен на увеличение риска на две единицы, если при этом доход операции увеличится не менее, чем на одну единицу. Определить для этого случая наилучшую операцию. Решение. Взвешивающая формула имеет вид f(i) = 2 f(1) = 2*29/6 – 20/6 = 6,33; f(2) = 2*25/6 – 4 = 4,33; f(3) = 2*7 – 7/6 = 12,83; f(4) = 2*17/6 – 32/6 = 0,33 Следовательно, лучшей является третья операция, а худшей – четвертая.
Тема 3. Измерители и показатели финансовых рисков Количественная оценка риска. Риск отдельной операции. Общие измерители риска.
В данной теме рассматриваются критерии и методы принятия решений в тех случаях, когда предполагается, что распределения вероятностей возможных исходов либо известны, либо они могут быть найдены, причем в последнем случае не всегда необходимо задавать в явном виде плотность распределения.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.176.111 (0.009 с.) |

 и средним ожидаемым доходом
и средним ожидаемым доходом  . Если ввести прямоугольную систему координат, на оси абсцисс которой откладывать значения
. Если ввести прямоугольную систему координат, на оси абсцисс которой откладывать значения 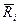 ,
,  ) взвешивающая формула имеет вид f(i) = 3
) взвешивающая формула имеет вид f(i) = 3 


