
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування і біматричних ігор. Рівноваги Нэша і ПаретоСодержание книги
Поиск на нашем сайте Розв’язування і біматричних ігор. Рівноваги Нэша і Парето
Біматричні ігри
Біматричні ігри – це неантогонистичні (з ненульовою сумою) однокрокові ігри двох або більше гравців при відсутності інформації. Біматричні ігризастовують в ситуаціях, коли інтереси гравців не строго протилежні, тобто хоча вони і не співпадають, але не обовязково протилежні. Для біматричної гри двох гравців формуються 2 матриці
Перша таблиця описує виграші гравця A, друга – гравця B. Стратегії A1 … Am гравця A – це рядки обох матриць, а стратегії B1 … Bn гравця В – це колонки обох матриць.
Тут A – платіжна матриця гравця A, а B – платіжна матриця гравця B.
Матриці біматричної гри взаємно логічно узгоджені – при співпадінні інтересів гравців значення відповідні елементи матриць однакові, при розбіжності – різні.
Гравець А обирає одну стратегію – рядок в обох матрицях, а гравець В обирає одну стратегію – колонку в обох матрицях. Виграшем гравця A є елемент матриці А на перетині обраних стратегій, виграшем гравця В є елемент матриці В на перетині обраних стратегій. Якщо гравець А обрав стратегію A1, а гравець В обрав стратегію B1, то виграш гравця A – елемент a11 матриці А, а виграш гравця В – елемент b11 матриці В.
Метою кожного гравця є збільшення свого виграшу.
Розв ’ язок біматричної гри повинен певним чином задовільняти обох гравців. Визначаються максимальні виграши кожного гравця, які не приводять до значних втрат інших гравців. Зокрема використовується поняття рівноваги – визначення стратегій гравців, при відхиленні від яких виграш відхиляющогося гравця зменшується.
При розв ’ язуванні гри у змішаних стратегіях, тобто при чередуванні (чистих) стратегій з певними частотами ці частоти мають вигляд: гравець A – стратегії A1,, Am з частотами p1, …, pm, де p1>=0, …,pm>=0, гравець B – стратегії B1, …, Bn з частотами q1, …, qn, де q1>=0,,…,qn>=0, При змішаних стратегіях в біматричних іграх середні виграші гравців A и B у загальному вигляді складають:
Тут Н – виграші гравців,
Розв ’ язування біматричних ігр з кількома учасниками і з кількома стратегіями є складною задачею і немає простої методики її розв ’ язування. Задача значно спрощується в випадку біматричної гри двох гравців з матрицями 2х2. Для розв ’ язування біматричних ігор застосовуються метод рівноваги Неша, метод оптимальності за Парето та інш.
Далі разглядаються біматричні ігри двох гравців з матрицями 2х2. Для цього випадку приймається позначення імовірностей використання стратегій: для А: p1 = p і p2 =1-p, для В: q1= q і q2=1-q. Якщо p = 1, то p1 = 1 і p2 = 0 – застосовується стратегія A1. Якщо p = 0, то p1 = 0 і p2 = 1 – застосовується стратегія A2. Аналогічно застосовуються стратегії B1 і B2.
Рівновага Нэша 1. Визначення. Рівноваги Неша існуютьдля всіх кінцевих ігор з будь-яким числом гравців.
Обчислення рівноваг Неша Для обчислень рівноваг в іграх з кількома учасниками і з кількома стратегіями немає простого рецепту. Це досить складний алгоритмПошук спрощується якщо в грі лише два гравці. Метод рівноваг Неша аналітично-графічний - на площину прямокутної системи координат (p, q) з квадратом розміром 0<=p<=1 і 0<=q<=1 потрібно нанести результати розрахунку у вигляді зігзага значень p і зігзага значень q. Точки перетину зігзагів є точками рівноваг Неша. Подробніше в наступному пункті. Висновок Ефект фокальної точки. Як показує гра «Сімейна суперечка» рівноваг Неша може бути кілька. Кожна з них має властивість, що самооправдовуючуюся властивістю. Що ж могло б змусити гравців обрати деяку специфічну рівновагу? Будь-яка річ, яка змушує їх фокусувати увагу саме на цій рівновазі. Шеллінг у своїй книзі «Стратегія конфлікту» назвав це ефектом фокальної точки. Це будь-яка властивість, що виділяє конкретн рівновагу серед інших. Ними можуть бути традиції, статус кво тощо. Також фокальна точка може визначатися властивостями функції корисності. Наприклад, «ділення доларів»: є 100 доларів. Кожен з гравців називає число від 0 до 100. Якщо сума <= 100, то кожен отримує, що просив, інакше - по нулях. Серед безлічі рівноваг, таких як (91,9) або (40,60) є фокальна - (50,50). Оскільки кожен гравець розуміє, що це ефективне і справедливе рішення (проте не завжди ефективне і справедливе рішення є рівноважним).
Оптимальність за Парето
Точки множини ω можна розбити на три клаcи: I клас – точки, які, залишаючись в множині ω, можна зсунути так, щоб одночасно збільшились обидві координати (в цей клас потрапляють всі внутрішні ІІ клас – точки, переміщенням яких по множині ω можна збільшити тільки одну з координат при збереженні значення другої (вертикальний відрізок АВі горизонтальний відрізок РQ на границі множини ω); III клас – точки, переміщення яких по множині ω можуть лише зменшити або одну із координат, або дві (дуга BQ границі множини ω). Множина точок третього класу називається множиною Парето або границею Парето даної множини ω.
Переглянемо один із методів, в якому використовується множина Парето – метод ідеальної точки: Нехай ми маємо деяку множину ε, кожна точка якого описується двома функціями U=Φ(x;y) і V=Ψ(x;y) (U і V – середні виграші іграків А і В, а x і y – ймовірність вибору стратегії для отримання цього виграшу). Тепер в даній множині ε спробуєм знайти таку точку, в якій обидві функції U і V приймають своє максимальне значення. В загальному випадку ця точка опинеться поза множиноюі ε. Тобто, не існує стратегій, при яких два гравці отримують максимальний для кожного виграш.
Точка, в якій функції U і V досягають своїх максимальних значень, называются точкою утопії.. Тому будується множина Парето і на ній знаходиться точка, найближча до точки утопії — ідеальна точка (див. рис.). Випливає рівність Р = Р*, q = q*. Тобто, в оптимальній по Парето ситуації гравці не можуть спільними зусиллями збільшити виграш одного із гравців, не зменшивши при цьому виграш другого.
Приклад: гра «Дилема в’язнів» Платіжні матриці в цій грі мають наступний вигляд
Для всіх можливих значень ймовірність p і q задані дві функції U=НА(p,q)= –pq – 9p(1 – q) – 6(1 – p)(1 – q), V= Нв(р,q)= – pq – 9(1 – p)q – 6(1 – p)(1 – q).
Завдання для перевірки засвоєного матеріалу
Задача «Студент-викладач» Вирішити приклад через рівновагу Неша і оптимальність за Парето.
Завдання
1. Засвоїти рівновагу Неша для дилеми в'язнів. 2. Обчислити рівновагу Неша для сімейної суперечки. 3. Засвоїти оптимальність Парето для дилеми в'язнів. 4. Обчислити задачу «Студент-викладач» 5. З матриці свого варіанту лабораторної 4 виділити 2 матриць 2х2: А - лівий верхній кут, B – правий нижній і розвязати біматричну гру методами рівноваги Неша і оптимальності Парето.
1985. 2. Крушевский А.В. Теория игр. Киев: "Вища Школа", 1977. Розв’язування і біматричних ігор. Рівноваги Нэша і Парето
Біматричні ігри
Біматричні ігри – це неантогонистичні (з ненульовою сумою) однокрокові ігри двох або більше гравців при відсутності інформації. Біматричні ігризастовують в ситуаціях, коли інтереси гравців не строго протилежні, тобто хоча вони і не співпадають, але не обовязково протилежні. Для біматричної гри двох гравців формуються 2 матриці
Перша таблиця описує виграші гравця A, друга – гравця B. Стратегії A1 … Am гравця A – це рядки обох матриць, а стратегії B1 … Bn гравця В – це колонки обох матриць.
Тут A – платіжна матриця гравця A, а B – платіжна матриця гравця B.
Матриці біматричної гри взаємно логічно узгоджені – при співпадінні інтересів гравців значення відповідні елементи матриць однакові, при розбіжності – різні.
Гравець А обирає одну стратегію – рядок в обох матрицях, а гравець В обирає одну стратегію – колонку в обох матрицях. Виграшем гравця A є елемент матриці А на перетині обраних стратегій, виграшем гравця В є елемент матриці В на перетині обраних стратегій. Якщо гравець А обрав стратегію A1, а гравець В обрав стратегію B1, то виграш гравця A – елемент a11 матриці А, а виграш гравця В – елемент b11 матриці В.
Метою кожного гравця є збільшення свого виграшу.
Розв ’ язок біматричної гри повинен певним чином задовільняти обох гравців. Визначаються максимальні виграши кожного гравця, які не приводять до значних втрат інших гравців. Зокрема використовується поняття рівноваги – визначення стратегій гравців, при відхиленні від яких виграш відхиляющогося гравця зменшується.
При розв ’ язуванні гри у змішаних стратегіях, тобто при чередуванні (чистих) стратегій з певними частотами ці частоти мають вигляд: гравець A – стратегії A1,, Am з частотами p1, …, pm, де p1>=0, …,pm>=0, гравець B – стратегії B1, …, Bn з частотами q1, …, qn, де q1>=0,,…,qn>=0, При змішаних стратегіях в біматричних іграх середні виграші гравців A и B у загальному вигляді складають:
Тут Н – виграші гравців,
Розв ’ язування біматричних ігр з кількома учасниками і з кількома стратегіями є складною задачею і немає простої методики її розв ’ язування. Задача значно спрощується в випадку біматричної гри двох гравців з матрицями 2х2. Для розв ’ язування біматричних ігор застосовуються метод рівноваги Неша, метод оптимальності за Парето та інш.
Далі разглядаються біматричні ігри двох гравців з матрицями 2х2. Для цього випадку приймається позначення імовірностей використання стратегій: для А: p1 = p і p2 =1-p, для В: q1= q і q2=1-q. Якщо p = 1, то p1 = 1 і p2 = 0 – застосовується стратегія A1. Якщо p = 0, то p1 = 0 і p2 = 1 – застосовується стратегія A2. Аналогічно застосовуються стратегії B1 і B2.
Рівновага Нэша 1. Визначення. Рівноваги Неша існуютьдля всіх кінцевих ігор з будь-яким числом гравців.
Обчислення рівноваг Неша Для обчислень рівноваг в іграх з кількома учасниками і з кількома стратегіями немає простого рецепту. Це досить складний алгоритмПошук спрощується якщо в грі лише два гравці. Метод рівноваг Неша аналітично-графічний - на площину прямокутної системи координат (p, q) з квадратом розміром 0<=p<=1 і 0<=q<=1 потрібно нанести результати розрахунку у вигляді зігзага значень p і зігзага значень q. Точки перетину зігзагів є точками рівноваг Неша. Подробніше в наступному пункті.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.012 с.) |


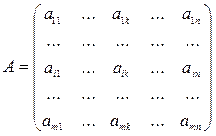
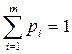 ,
,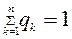 .
.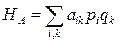

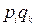 - частоти змішаних стратегій гравця А і гравця В.
- частоти змішаних стратегій гравця А і гравця В.

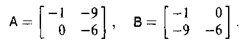
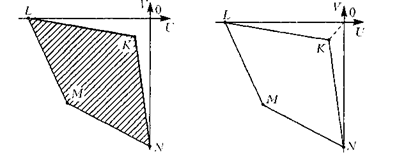 Точки з координатами (U,V), обчисленими по наведених формулах, на площині (U,V) заповнюють чотирикутник з вершинами K(– 1, –1), L(–9,0), M(–6, –6), N(0, –9) (див. рис.) Границя Парето цієї множини – ламана NKL.
Точки з координатами (U,V), обчисленими по наведених формулах, на площині (U,V) заповнюють чотирикутник з вершинами K(– 1, –1), L(–9,0), M(–6, –6), N(0, –9) (див. рис.) Границя Парето цієї множини – ламана NKL.



