
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування біматричних ігор 2Х2Содержание книги
Поиск на нашем сайте
Під вирішенням розуміється пара оптимальних стратегій (чистих або змішаних) і середній виграш кожного з гравців. Платіжні матриці гравців мають наступний вигляд:
Імовірності використання стратегій для А: p1 = p и p2 =1-p і для В: q1= q и q2=1-q. Середні виграші обчислюються за формулами:
HA (p,q) = a11 pq + a12 p(1 – q) + a 21(1 – p)q + a22 (1 - p)(1- q) HВ (p,q) = b11 pq + b12 p(1 – q) + b21(1 – p)q + b22(1 – p)(1 – q), де 0 < = p < = 1 і 0 < = q < = 1.
Пара чисел (p *, q *), де 0 <= p * <= 1 і 0 <= q * <= 1 визначає рівноважну ситуацію, якщо для будь-яких p і q, підпорядкованих умовами 0 <= p <= 1 і 0 <= q <= 1, одночасно виконані наступні нерівності:
HB (p*, q) <= HB (p*, q*) (1) (1)
С = a11 - a12 - a21 + a22, α = a22 - a12, D =b11 - b12 - b21 + b22 β = b22 - b21
Розглянемо приклад. «Дилема в'язнів»
Відповідні матриці:
Найдемо С, D, α, β: С = a11 - a12 - a21 + a22, α = a22 - a12, С = -1 - (-9) - 0 + (-6) = 2 α = - 6 - (-9) = 3
D =b11 - b12 - b21 + b22 β = b22 - b21 D = - 1- 0 - (-9) + (-6) = 2 β = - 6 - (- 9) = 3.
Підставимо С, D, α, β в нерівності (2): (р - 1) (Cq - α)> = 0 p (Cq - α)> = 0 (p – 1) (2q – 3)>=0 і p(2q – 3)>= 0 – ліва пара нерівностей
(q - 1) (Dp - β)> = 0 q (Dp - β)> = 0
Для лівої пари нерівностей розглянемо три можливі випадки: 1) p = 0, 2) p = 1, 3) 0 <= p <= 1 Отримуємо: 1. p=0: (р - 1) (Cq - α)=(0-1)(2q - 3)= - 2q + 3 >= 0, звідки q <= 3/2, p(Cq - α)=0*(2q – 3)= 0 2. p=1: (р - 1) (Cq - α)=0*(2q - 3) = 0, p(Cq - α)=1* (2q - 3)= 2q - 3 >= 0, звідки q >= 3/2 3. 0<=p<=1: Розв ’ язується для p=0 і p=1 і беруться до уваги результати адекватні для обох варіантів. З п.1 для p = 0: q <= 3/2, з п.2 для p=1: q >= 3/2, тобто для двох варіантів одночасно виконується тільки умова рівності, звідки звідки q = 3/2
Для правої пари нерівностей є також три випадки: 1) q = 0, 2) q = 1, 3) 0 <= q <= 1 Відповідно отримуємо: 1. q = 0: (q - 1) (Dp - β)=(0-1)(2p - 3)= - 2p + 3 >= 0, звідки p <= 3/2; q (Dp - β)>= 0*(2q – 3)= 0 2. q = 1: (q - 1) (Dp - β)= 0*(2p – 3)= 0 q (Dp - β)>= 1*(2p – 3)= 2p – 3 >= 0, звідки p >= 3/2 3. 0 <= q <= 1: Розв ’ язується для q =0 і q =1 і беруться до уваги результати адекватні для обох варіантів. З п.1 для q = 0: p <= 3/2, з п.2 для q =1: p >= 3/2, тобто для двох варіантів одночасно виконується тільки умова рівності, звідки p = 3/2
Нанесемо отримані результати на площину прямокутної системи координат (p, q) з виділеним на ній одиничним квадратом, відповідним нерівностям:0<=p<=1 і 0<=q<=1. Зигзаги, що складаються з трьох прямих, відповідних 3-м розглянутим випадкам для кожної нерівності перетинаються в точці з координатами (0,0). Це і є точка рівноваги. Вона задовольняє всім вимогам. Цій точці відповідають змішані стратегії P = (0,1) і Q = (0,1), тобто насправді точці відповідають другі чисті стратегії обох гравців - «говорити». Стратегії визначені так. Для точки (0,0) перетину зигзагів p=0 і q=0, тобто p1=p=0 і p2 =1-p=1, q1= q=0 і q2=1-q=1, тому обом гравцям потрібно застосувати другі чисті стратегії. Виграш кожного з них складе у результаті (–6).
Також можна обчислити середній виграш для p=0 і q=0. HA (p,q) = a11 pq + a12 p(1 – q) + a 21(1 – p)q + a22 (1 - p)(1- q) HВ (p,q) = b11 pq + b12 p(1 – q) + b21(1 – p)q + b22(1 – p)(1 – q)
HA (0,0) = -1*0*0 - (-9)*0*1 - 0 + (-6) *1*1 =-6 HВ (0,0) = -1*0*0 - 0 - (-9)*0*1 + (-6) *1*1 =-6
Визначення виграшу застосуванням обчислених чистих стратегій і за формулами дає однаковий результат.
Розглянемо інший приклад. «Сімейна суперечка»
Провівши всі обчислення і дослідження аналогічно попереднього прикладу, отримаємо:
p = 2/3, q = 1/3 з середніми виграшами HA (2/3, 1/3) = 2/3 і HB (1/3, 2/3) = 2/3 Висновок Ефект фокальної точки. Як показує гра «Сімейна суперечка» рівноваг Неша може бути кілька. Кожна з них має властивість, що самооправдовуючуюся властивістю. Що ж могло б змусити гравців обрати деяку специфічну рівновагу? Будь-яка річ, яка змушує їх фокусувати увагу саме на цій рівновазі. Шеллінг у своїй книзі «Стратегія конфлікту» назвав це ефектом фокальної точки. Це будь-яка властивість, що виділяє конкретн рівновагу серед інших. Ними можуть бути традиції, статус кво тощо. Також фокальна точка може визначатися властивостями функції корисності. Наприклад, «ділення доларів»: є 100 доларів. Кожен з гравців називає число від 0 до 100. Якщо сума <= 100, то кожен отримує, що просив, інакше - по нулях. Серед безлічі рівноваг, таких як (91,9) або (40,60) є фокальна - (50,50). Оскільки кожен гравець розуміє, що це ефективне і справедливе рішення (проте не завжди ефективне і справедливе рішення є рівноважним).
Оптимальність за Парето
Точки множини ω можна розбити на три клаcи: I клас – точки, які, залишаючись в множині ω, можна зсунути так, щоб одночасно збільшились обидві координати (в цей клас потрапляють всі внутрішні ІІ клас – точки, переміщенням яких по множині ω можна збільшити тільки одну з координат при збереженні значення другої (вертикальний відрізок АВі горизонтальний відрізок РQ на границі множини ω); III клас – точки, переміщення яких по множині ω можуть лише зменшити або одну із координат, або дві (дуга BQ границі множини ω). Множина точок третього класу називається множиною Парето або границею Парето даної множини ω.
Переглянемо один із методів, в якому використовується множина Парето – метод ідеальної точки: Нехай ми маємо деяку множину ε, кожна точка якого описується двома функціями U=Φ(x;y) і V=Ψ(x;y) (U і V – середні виграші іграків А і В, а x і y – ймовірність вибору стратегії для отримання цього виграшу). Тепер в даній множині ε спробуєм знайти таку точку, в якій обидві функції U і V приймають своє максимальне значення. В загальному випадку ця точка опинеться поза множиноюі ε. Тобто, не існує стратегій, при яких два гравці отримують максимальний для кожного виграш.
Точка, в якій функції U і V досягають своїх максимальних значень, называются точкою утопії.. Тому будується множина Парето і на ній знаходиться точка, найближча до точки утопії — ідеальна точка (див. рис.).
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.174.32 (0.008 с.) |



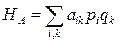



 Гра має три точки рівноваги. Дві чистих і одна змішана. Всі вони відповідають вимогам.
Гра має три точки рівноваги. Дві чистих і одна змішана. Всі вони відповідають вимогам. 




