
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прийняття рішень у полі шостої інформаційної ситуаціїСодержание книги
Поиск на нашем сайте
Нагадаємо, що ця ситуація характеризується наявністю чинників, які зумовлюють «проміжну» між п’ятьма розглянутими вище інформаційними ситуаціями поведінку економічного середовища щодо вибору своїх станів. Класичними прикладами критеріїв прийняття компромісних рішень у полі шостої інформаційної ситуації є критерій Гурвіца, модифіковані критерії та критерій Ходжеса-Лемана [6; 7; 9; 11]. 1) Критерій Гурвіца. Гурвіц запропонував використовувати зважену комбінацію найкращого та найгіршого. Такий підхід до вибору рішень відомий як критерій показника песимізму-оптимізму. Особливістю цього критерію є те, що в ньому передбачається не повний, а частковий антагонізм середовища та СПР. Згідно з критерієм Гурвіца, у випадку, коли F =
Величину У випадку, коли
Параметр l в обох випадках можна інтерпретувати як коефіцієнт несхильності до ризику. 2) Модифіковані критерії. Згідно з модифікованими критеріями,у випадку, коли F =
або у випадку, коли F =
де 3) Критерій Ходжеса-Лемана. Ходжес та Леман стоять на тій позиції, що в практиці прийняття рішень за умов невизначеності інформація про стан ЕС перебуває між повним незнанням та точним знанням апріорного розподілу. Критерій Ходжеса-Лемана дає змогу використовувати всю інформацію, яку має суб’єкт управління, і водночас забезпечує заданий рівень гарантії у випадку, коли ця інформація неточна. У певному плані критерій Ходжеса-Лемана являє собою «суміш» критеріїв Байєса та Вальда. Згідно з критерієм Ходжеса-Лемана, у випадку, коли F =
Якщо
Як і раніше, параметр lÎ[0;1], і його можна інтерпретувати як коефіцієнт несхильності до ризику. 36. Класи задач прийняття багатоцільових рішень за умов невизначеності та ризику. Перша задача прийняття багатоцільових рішень в умовах ризику. Нехай суб'єкт керування має
Друга задача. Нехай суб'єкт керування має Третя задача. Нехай суб'єкт керування в ситуації прийняття рішень Четверта задача. Нехай суб'єкт керування перебуває в ситуації прийняття рішень 37. Структурна схема процесу побудови моделі багатокритеріальних задач.
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.71.135 (0.008 с.) |

 оптимальним є рішення:
оптимальним є рішення: .
. називають l -показником Гурвіца для рішення sk Î S.
називають l -показником Гурвіца для рішення sk Î S. , оптимальним є рішення:
, оптимальним є рішення: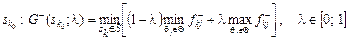 .
. ,
, рішення:
рішення: ,
, ;
; 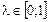 , а як величину
, а як величину  можна використати середньоквадратичне
можна використати середньоквадратичне  , семіквадратичне
, семіквадратичне  відхилення тощо. Параметр
відхилення тощо. Параметр  , який використовують у зазначених вище критеріях, можна тлумачити як коефіцієнт несхильності СПР до ризику.
, який використовують у зазначених вище критеріях, можна тлумачити як коефіцієнт несхильності СПР до ризику. .
. то оптимальним рішенням є:
то оптимальним рішенням є: .
. ситуацій прийняття рішень
ситуацій прийняття рішень  ,
,  ,…,
,…,  , що відрізняються одна від одної функціоналом оцінювання (прибуток, затрати тощо) у заданій інформаційній ситуації
, що відрізняються одна від одної функціоналом оцінювання (прибуток, затрати тощо) у заданій інформаційній ситуації  . Потрібно визначити оптимальне рішення для всіх
. Потрібно визначити оптимальне рішення для всіх  ситуацій прийняття рішень одночасно. Скориставшись основними факторами
ситуацій прийняття рішень одночасно. Скориставшись основними факторами  прийняття багатоцільових рішень, можна дістати ситуацію прийняття рішень з одним скалярним функціоналом оцінювання для заданої інформаційної ситуації
прийняття багатоцільових рішень, можна дістати ситуацію прийняття рішень з одним скалярним функціоналом оцінювання для заданої інформаційної ситуації  та обраного критерію прийняття рішень.
та обраного критерію прийняття рішень.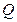 ситуацій прийняття рішень
ситуацій прийняття рішень  , що відрізняються одна від одної функціоналом оцінювання. Нехай також для всіх
, що відрізняються одна від одної функціоналом оцінювання. Нехай також для всіх  . Застосувавши цей критерій, у кожній із розглядуваних ситуацій дістанемо випадок прийняття багатоцільових рішень
. Застосувавши цей критерій, у кожній із розглядуваних ситуацій дістанемо випадок прийняття багатоцільових рішень  , де
, де  . Вибір основних чинників
. Вибір основних чинників  має певну інформаційну ситуацію
має певну інформаційну ситуацію  . З множини
. З множини  . Застосовуючи кожний з цих критеріїв
. Застосовуючи кожний з цих критеріїв  до даної ситуації прийняття рішень, для кожного розв'язку
до даної ситуації прийняття рішень, для кожного розв'язку  дістаємо вектор оцінок
дістаємо вектор оцінок  , тобто йдеться про ситуацію прийняття багатоцільових рішень, в якій оптимальний розв'язок обирається так само, як у другій задачі прийняття багатоцільових рішень.
, тобто йдеться про ситуацію прийняття багатоцільових рішень, в якій оптимальний розв'язок обирається так само, як у другій задачі прийняття багатоцільових рішень. , і причому виділено Q інформаційних ситуацій. Для кожної з них органом управління виділяється один критерій прийняття рішення
, і причому виділено Q інформаційних ситуацій. Для кожної з них органом управління виділяється один критерій прийняття рішення  . Застосувавши кожний з обраних критеріїв, дістанемо ситуацію прийняття багатоцільових рішень.
. Застосувавши кожний з обраних критеріїв, дістанемо ситуацію прийняття багатоцільових рішень.


