
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Часовий критерій ризику і його значенняСодержание книги
Поиск на нашем сайте
Вище ми розглядали критерії, що характеризують випадковий характер величин і процесів, що визначають ризик. Серед причин виникнення ризику, як наслідок невизначеності, найбільш постійної і істотної є тривалість часового інтервалу, протягом якого відбувається процес або явище – джерело ризику. Будь-який процес відбувається в часі, тому параметр-час бере участь у формуванні практично будь-якого ризику. Найбільш застосовними кількісними критеріями ризику є: ймовірність втрати ресурсу і середньоквадратичне відхилення величини втрати. Тому було б вельми корисним визначити вплив часового чинника на величину цих критеріїв. Часовий чинник найістотніше виявляється в банківських операціях. Основні операції банку - кредитування, інвестування, емісія цінних паперів – бувають досить тривалими. Оскільки часовий чинник буває не єдиною причиною ризику (швидше час виступає як каталізатор прояву чинників ризику), то доцільно залежність рівня ризику від часу визначити параметрично: параметр "час" включається у формулу розрахунку величин критерію, що не виключає впливу решти чинників-причин. Не вимагає доказу той факт, що критерій ризику банківської операції параметрично залежить від часу. Міркування здорового глузду наочно підтверджують таку залежність: кредит банку, виданий на рік, супроводжується більшим ризиком, ніж кредит такого ж об'єму, виданий на половину року. Майже безризиковими можна розглядати тільки кредити, які гарантує ідеальний поручитель (держава). У літературі і навіть в нормативних документах ризик часто визначається без посилання на залежність від часу, хоча таке визначення є не точним. Мабуть, в даних випадках часовий чинник встановлюється за умовчанням. У банківських операціях розмір ризику указується з розрахунку на часовий інтервал тривалістю в один рік. Проте, жорстке завдання величини часового інтервалу часто є незручним, оскільки значне число банківських операцій не кратні цілому числу років. Тому зручнішим для використовування є не ймовірність ризику, а функція часу, визначаюча ризик R(t) (при t=1 рік R(t) визначає ймовірність втрати кредиту протягом одного року). Якщо R(t) – ймовірність несприятливого результату (ризику), то 1- R(t)= Р(t) – ймовірність сприятливого результату.
Обґрунтуємо вид функції R(t)(Р(t)). Перш за все, очевидно: R(о)=0, R(?)> 1. Крім того відзначимо, що подія ризику може бути викликане багато разів і несподівано з часом t. Такі події звичайно підкоряються закону Пуассона, який описується формулою:
де Для закону Пуассона математичне очікування (m) і дисперсія σ2 визначаються у вигляді залежності:
Залишається вирішити два питання: як застосувати закон для визначення R(t), і чи відображає цей закон суть часової функції ризику. Розглянемо ці питання послідовно. 1. R(t)= 1-P(t), P(t) – ймовірність ненастання події ризику. При m? 1такое подій наступає. Тому, якщо P(t) = е-а, то R(t) = 1- е-а. 2. Для відповіді на друге питання потрібно перевірити, чи виконуються властивості часової функції ризику. По-перше, а - математичне очікування числа подій в одиницю часу. Розділимо довільний відрізок часу Т на k частин. Виходячи з властивостей функції ризику (якщо ні в одному з до відрізків не відбулося подія ризику, то результат ситуацій сприятливий):
Якщо ж хоча б в одному з до ділянок відбулася подія ризику, то:
Для кожного конкретного випадку R(t) і λ різні. Хай відомо, що для Т=1год R(t) = е-λt = R0, тоді:
Так, для Р =0,05 λ = -0,0513. Остаточно одержуємо:
Розглянемо можливість отримання виразу часової функції ризику для критеріїв: m – математичне очікування втрат і σ – СКВ об'єму втрат (дисперсний критерій). Одержати ці вирази виявляється складнішою задачею, оскільки потрібно визначити залежність від часу характеру закону розподілу ймовірності.
7. Часова залежність дисперсного критерію ризику
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.180 (0.007 с.) |


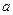 – параметр закону Пуассона; Рm – ймовірність виникнення рівно m подій ризику при параметрі а (а=λt).
– параметр закону Пуассона; Рm – ймовірність виникнення рівно m подій ризику при параметрі а (а=λt).








