
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення ефективності інвестуванняСодержание книги
Поиск на нашем сайте
У практичній банківській діяльності кількісні співвідношення між параметрами визначення доходу (формули (6), (8)) часто не використовуються, хоча якісно вони враховуються. Значення Fj визначає прибутковість, Nj позначає процентну ставку за кредит, час tj визначає термін надання кредиту. У приведених формулах і практичних результатах банківської діяльності показана залежність ризикованої і часу надання кредиту, що повинне збільшити процентну ставку за кредит. Термін надання кредиту tj двояко впливає на прибутковості операції кредитування: із зростанням tj зростає майбутня вартість грошей, що корисне і позичальнику і кредитору. Цей процес управляється за допомогою ставки дисконту (I). З другого боку, із зростанням tj зростає значення функції ризику. Цей вплив встановлює формула (6). Якщо зафіксувати рівень прибутковості кредиту F* на термін tj = 1 рік і вважати його нормативним, величина процентної ставки визначається співвідношенням:
Для встановлення залежності Fj від параметрів побудуємо графік залежності Fj(tj) при наступних параметрах, показаних в табл.4.3.
Таблица 4.3. Параметры функции Fj(tj).
При розрахунках в табл.4.3. прийнято I =0,1. По характеру залежностей можна зробити висновки: 1.Криві ефективності різко знижують свої значення із зростанням tj, особливо при великих ризиках. 2.Ефективність кредитів при великих tj > 3 практично падає до нуля навіть при невеликих ризиках (0,1 в рік). 3.Використовування постійного значення процентної ставки після кредитів без урахування часу виділення ресурсу невиправдане навіть при короткострокових і середньострокових кредитах (0,5 роки). 4.Тривалість кредиту сильно впливає на його ефективність. Так при tj≥2 роки удвічі більший кредит оплачується майже як удвічі менший. 5.При наданні середньо і довгострокових кредитів банк повинен або піднімати процентну ставку (формула (11)), або кредитувати високо надійних клієнтів (0,01-0,02 в рік). Навіть при Р = 0,05 на рік при tj = 3 роки ефективність падає на ⅓. 6.Процентна ставка може бути визначена по формулі (11). Лекція 5 Оцінка ситуації в умовах ризику
Питання лекції: 1.Теорія корисності. 2.Корисність по Нейману. 3.Відношення до ризику суб'єкта управління ризиком. 4.Премія за ризик. 5.Методика розрахунку премії за ризик.
Література: [6-9, 13].
Оцінка ситуації і, відповідно, стратегія поведінки в цій ситуації в умовах ризику істотно залежать від методів і критеріїв оцінки суб'єктом управління ризиком корисності його виборів і відношення до ризику. Розглянемо докладніше ці поняття.
Теорія корисності Корисність означає ступінь задоволення суб'єкта від виконання деякої дії. Корисність – це використовуваний критерій в теорії Прийняття рішень. Найзагальніший підхід при встановленні ступеня оцінки ризику полягає у введенні функції корисності (Ф.П.). Будь-яке рішення (дія) в умовах ризику не може бути однокритерійним. Будь-який критерій (дохід, втрати, ймовірність отримання доходу, СКВ отримання доходу) сприймається через призму ризику, а ризик – слідство невизначеності. Корисність і дохід не тотожні, але їх взаємовідношення прозоре: корисність прямо пропорційна доходу. Зв'язок же корисності з ризиком не так очевидний, тим паче, що: а) корисність прямо пропорційна доходу; б) дохід і рівень ризику зв'язані (Марковіц): чим більше дохід, тим менше ризик і навпаки. Ставиться в цих умовах задача: як сумістити оцінку корисності і рівень ризику? Не дивлячись на наявність взаємозв'язку, корисність і дохід не тотожні, їх співвідношення сильно залежить від ситуації. Для оцінки ступеня корисності вводяться різні поняття, зокрема саме поняття " полезность",например, " пріоритетність". При оцінці корисності часто використовуються нерядкові оцінки: 1) більш пріоритетне, ніж - > 2) байдуже - ~ 3) не гірше, ніж - ≥ Поняття корисності носить, як правило, суб'єктивний характер. Для різних суб'єктів одне і теж кількість товару або чого-небудь ще може мати різну корисність. У теорії корисності важливе значення має поняття " гранична корисність"- додаткова корисність при споживанні додаткової кількості товару. Залежить від попередньої кількості. Приклад: перші 5 плиток шоколаду мають більшу корисність, ніж 5 подальших плиток і т.д. Граничну корисність звичайно вимірюють при отриманні додаткової одиниці товару (блага).
2.Корисність по Нейману Корисність по Нейману оцінюється за допомогою лотереї, яка визначає, одержати х* з вірогідністю (1-р) або х* з вірогідністю р. Величини виграшу в лотерею х* і х* вибираються так, що что х*≡ х, х*< х, для всіх х х* - найпріоритетніше значення виграшу. Експерту пропонують вибір: одержати суму х або виграш в лотерею. Під лотереєю розуміється ситуація виграшу х* з вірогідністю р або х* з вірогідністю (1-р). Лотерея L (х*, р(х), х*). Значення р змінюються до тих пір, поки значення х і виграш в лотерею приблизно порівняються. Очікуваний виграш в лотерею L (лотерея має N виграшів, І – корисність):
Справедлива головна формула теорії очікуваної корисності:
Поняття " певного еквівалента" лотереї L є одним з основних при розгляді різних характеристик ризику і їх взаємозв'язку з функціями корисності. Певний еквівалент лотереї L – це гарантована сума, отримання якої еквівалентне участі в лотереї, тобто
Якщо можливі виграші описуються щільністю розподілу φ(υ), то очікуваний виграш в лотереї рівний:
а певний еквівалент
Певний еквівалент – суб'єктивна оцінка лотереї на основі оцінок очікуваних результатів. Приклади функції корисності (певного еквівалента). 1.Зростаюча функція для суб'єкта, байдужого до ризику: І(х)= а + вх; у > 0. 2. Зростаюча функція для суб'єкта, не схильного до ризику: І(х)= log(x + у), х > -в. 3.Зростаюча функція з несхильністю до ризику: И(х) = а – ве-сх, в > 0, х ≥ 0. 4. Зростаюча функція з схильністю до ризику: И(х) = а – ве-сх, в > 0, х ≥ 0.
По своїй фізичній суті премія за ризик (надбавка за ризик) – це сума (у одиницях вимірювання критерію х – виграш або збиток), якої суб'єкт управління ризиком згоден пожертвувати з середнього виграшу, щоб уникнути ризику (платня за ризик), пов'язаного з лотереєю. 3.Відношення до ризику суб'єкта управління ризиком Суб'єкта називають несхильним до ризику, якщо для нього пріоритетніше одержати гарантовано очікуваний виграш в лотерею, ніж брати в ній участь. Оскільки корисність лотереї співпадає з математичним очікуванням корисності і випадкових результатів, та умова несхильності до ризику має вигляд:
де х – випадкова величина виграшу, залежна від результату ω. Різниця між очікуваним виграшем і певним еквівалентом
Страховою сумою (СС) називають величину певного еквівалента з протилежним знаком:
Умови відношення суб'єкта управління ризиком до ризику: 1) 2) 3) де
Оскільки для байдужості до ризику
і вони співпадають, то функція І(х) – лінійна. Якщо особа нейтральна до ризику – функція корисності лінійна. Для особи, несхильної до ризику, привабливішим є отримання гарантованої суми (середній виграш лотереї), тобто
Функція, що задовольняє цьому рівнянню, називається увігнутою (опуклої вгору). Особа, несхильна до ризику, має опуклу вгору функцію корисності.
Рис.5.1. Залежність ризику для особи, несхильної до ризику.
Для особи, схильної до ризику, виконується умови:
Цій умові задовольняє опукла (опукла вниз) функція. Особа, схильна до ризику, має опуклу вниз функцію корисності.
Рис.5.2. Залежність ризику для особи, схильної до ризику.
Премія за ризик Певний еквівалент (позначимо його через d) може брати участь у визначенні премії за ризик. Премія за ризик (r) – різниця між очікуваним виграшем і певним еквівалентом:
Премія r > 0 - при несхильності до ризику і r < 0 - при схильності до ризику. Розглянемо лотерею В цьому випадку можна записати:
оскільки
Якщо r(х) постійна і не залежить від х, то говорять, що є постійний ступінь ухилення від ризику. Цю характеристику можна сформулювати у вигляді: при постійному ступені ухилення від ризику премія за ризик не залежить від масштабу ризикованої операції. Аналогічно використовується поняття зростаючого і спадаючого ступеня ухилення від ризику. У приведених позначеннях на величину r впливає величина Δ, а також певний еквівалент
де σ2(Δ) – дисперсія лотереї, залежна від Δ. Коефіцієнт r(Δ) називається коефіцієнтом Пратта-Ерроу локальної абсолютної несхильності до ризику. Він показує ступінь впливу дисперсії ризикованої операції (об'єктивного чинника) на ступінь ризику. Для особи, несхильної до ризику, r (Δ) > 0. Криві байдужості. Функція корисності визначається одним з двох способів: 1. Функція корисності одного аргументу И(х), якщо є J результатів ситуації і I – масштаби операції, то:
2. Функція корисності двох аргументів И(Еi, σi), де Еi, σi, σi – математичне очікування і СКВ i -го рішення (ситуації). Функція І враховує відношення об'єкту до ризику. У загальному випадку вона нелінійна, оскільки премія за ризик зростає при підвищенні рівня ризику. Часто використовують функцію вигляду: Вид функції Е = f(у) показаний на малюнку (несхильний до ризику).
Рис.5.3. Криві байдужості. Залежності для особи, нейтральної до ризику, - лінійні. Кожна особа має свій графік байдужості функції Иi. З кривої видно, що дохід (Е) зростає разом з рівнем ризику (σ).
Рис.5.4. Криві байдужості. Криві байдужості можна трактувати як різні значення функцій корисності. Наприклад, крива 1 описує всі можливі норми прибутку (Еi) і ризику (σi). Переміщення по кривій означає збереження рівня корисності (Иi) і виражає зміну норми прибутку і ступеня ризику.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.008 с.) |

 (11)
(11)
 Х,, тобто х* - якнайменше пріоритетне значення виграшу;
Х,, тобто х* - якнайменше пріоритетне значення виграшу;

 - корисність ансамблю результатів співпадає з математичним очікуванням корисності результатів.
- корисність ансамблю результатів співпадає з математичним очікуванням корисності результатів.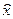 ~ L. Значення
~ L. Значення  або
або 



 називають премією за ризик.
називають премією за ризик.
 - несхильність до ризику;
- несхильність до ризику; - схильність до ризику;
- схильність до ризику; - байдужість до ризику,
- байдужість до ризику,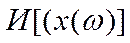 - функція корисності результату ω.
- функція корисності результату ω.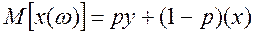 (очікуваний виграш),
(очікуваний виграш),









 (i – ій результат).
(i – ій результат). , де ω – премія за ризик (ω > 0 – несхильний до ризику; ω = 0 – нейтральний; ω < 0 – схильний до ризику).
, де ω – премія за ризик (ω > 0 – несхильний до ризику; ω = 0 – нейтральний; ω < 0 – схильний до ризику).




