
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Економічний ризик і його причини. УправлінняСодержание книги
Поиск на нашем сайте З М І С Т. Лекція 1. Економічний ризик і його причини. Управління ризиком 4
Лекція 2. Система кількісних оцінок економічного Ризику 11
Лекція 3. Порівняльна оцінка кількісних критеріїв оцінки ризику 23
Лекція 4. Розподіл ресурсів в часі і з урахуванням Ризику 26
Лекція 5. Оцінка ситуації в умовах ризику 37
Лекція 6. Управління ризиком 43
Лекція 7. Прийняття економічних рішень в умовах Ризику 49
Лекція 8. Багатоцільові рішення і математичне програмування в умовах ризику 55
Література
Лекція 1 Економічний ризик і його причини. Управління Ризиком
Питання лекції:
1. Введення. 2. Основні причини виникнення ризику. 3. Класифікація ризиків. 4. Управління ризиками.
Література: [1-4, 6-10, 12]
Введення Ситуації, в яких ризик відсутній, на практиці зустрічаються украй рідко. Рішення і дії в економіці засновані на взаємодії з численними і динамічними економічними чинниками (ціни, попит, асортимент товарів, виробничі ресурси). Характеристики цих чинників не тільки динамічні, але їх динаміка важко прогнозована і не виключає різких змін. Все це створює умови невизначеності щодо параметрів навколишнього середовища і поведінки економічних суб'єктів. Ризики, супроводжуючі господарську діяльність підприємства, складають великий портфель ризиків. Рівень ризику зростає з розширенням об'єму диверсифікації діяльності підприємства, з прагненням менеджерів підвищити рівень прибутковості, з освоєнням нових технологій і інструментів, з розширенням ринкової ніші підприємства. Рівень ризику робить серйозний вплив на багато аспектів господарської діяльності, проте, найбільш значимий його вплив виявляється в двох напрямах: • рівень ризику надає визначальну дію на формування рівня прибутковості операційної діяльності підприємства – ці два показники знаходяться в тісному взаємозв'язку і представляють єдину систему "прибутковість - ризик "; • фінансовий ризик є основною формою генерації прямої загрози банкрутства підприємств, оскільки фінансові втрати, пов'язані з ризиком, є найвідчутнішими. Ризики, супроводжуючі діяльність підприємств, є об'єктивними, постійно діючими чинниками у функціонуванні будь-якого підприємства і тому вимагають серйозної уваги з боку фінансових менеджерів. Облік чинників ризику в процесі управління фінансовою діяльністю підприємства супроводжує підготовку практично всіх управлінських рішень. Концепція обліку чинників ризику полягає в об'єктивній оцінці його рівня з метою забезпечення необхідного рівня прибутковості операцій і розробки системи заходів, що мінімізують його негативні фінансові наслідки для господарської діяльності підприємства. В умовах переходу до ринкової економіки повною мірою реалізується теза: немає нічого більш постійного на ринку, ніж зміни. У зв'язку з формуванням ринкових відносин поняття ризику міцно входить в наше життя. Це поняття повною мірою визначається невизначеністю зовнішнього середовища і всіх взаємозв'язаних чинників, які взаємодіють з лицем, що ухвалює рішення (ОПР). Невизначеність зовнішнього середовища є функцією кількості інформації, яку використовує ОПР. Чим це кількість менше, тим ризик і невизначеність, що його обумовлює виявляються великими. У деякому роді невизначеність адекватна терміну " ептропія", яка у фізиці і теорії інформації має чітку кількісну інтерпретацію. Отримання інформації про процес знижує ептропію про цей процес. Тому отримання інформації або підвищення інформованості ОПР знижує невизначеність, а, отже, і рівень ризику. Невизначеність про результат передбачуваного процесу або події може означати незнання про сприятливий (позитивному) або несприятливий (небезпечному, негативному) результат. Поняття ризику, як правило, відноситься до очікування або припущення саме несприятливого результату. У словнику Ожегова визначено: ризик – можливість небезпеки, невдачі, хоча невизначеність супроводжує і сприятливі події (виграш в лотерею, вдала зустріч і т.п.). У реальному житті велике значення мають подвійні події. Подвійність – атрибут практично будь-якого ризикованого явища. Людина ніколи б не ухвалювала ризикованих рішень, якби вони не мали позитивного результату. При позитивному результаті суб'єкт ризику опиняється у виграшній ситуації серед своїх конкурентів: результат є несподіваним і володар його стає володарем переваг або набагато випереджає конкурентів; у невизначеного результату звичайно розмір можливих втрат означає можливість більшого розміру виграшу. Недаремно є приказка: хто не ризикує – той не п'є шампанського. Прихильники ризику часто стають банкротами, але вони ж стають і виключно багатими людьми. У словнику по кібернетиці приведене визначення : ризик – це величина, що характеризує втрати або збитки, викликані неправильними або неточними рішеннями. Найяскравіше ризик виявляється в банківській діяльності - кожна банківська операція – джерело ризику. Сама суть банківської діяльності неможлива без ризику. Сучасний фінансовий ринок немислимий без ризику. Ризик присутній в будь-якій операції, тільки він може бути різних масштабів і по-різному "лагідніти", компенсуватися. Для банківської і будь-якої іншої економічної діяльності важливим є не уникнення ризику взагалі, а передбачення і зниження його до мінімального рівня – в цьому і полягає суть управління ризиком. Ігнорування ризику може мати дуже важкі наслідки, ризик потрібно прийняти, передбачати і управляти ним. У ланцюжку цих заходів на початку знаходиться аналіз ризику. Призначення аналізу: визначити рівень необхідної інформації для Прийняття рішення про доцільність участі в передбачуваній економічній діяльності (проекті), передбачити заходи захисту від можливих збитків. Аналізувати, ідентифікувати, оцінювати, оптимізувати ступінь ризику необхідно у випадках: • перед прийняттям стратегічних, інноваційних, інвестиційних рішень; • при стабілізації портфеля при виконанні угод; • при профілактичній діагностиці портфеля; • при необхідності отримання кредиту і привернутих інвестицій; • при прогнозуванні кон'юнктура і поведінки; • при маркетингових дослідженнях (прогноз попиту, поведінки споживачів); • при аргументуванні дозволу конфліктних ситуацій; • при аудиті і консалтингу. Системний аналіз ризику призначений для виявлення і оцінювання всіх його аспектів, вивчення суті процесів у зв'язку з виникненням ризику. Підприємницька діяльність завжди супроводжується ризиком на всіх стадіях виробничого процесу: від покупки і доставки сировини і комплектуючих до продажу продукції. Взаємозв'язок між ризиком і прибутком має фундаментальне значення для розробки ефективного менеджменту. Виправданий ризик – необхідний атрибут в стратегії і практиці ефективного менеджменту. Найефективніші методи управління ризиком визначаються на основі методології системного аналізу.
Об'єктом ризику називають економічну систему, ефективність і
умови функціонування, які наперед невідомі повною мірою. Під суб'єктом ризику розуміють особу (або колектив ), зацікавлені в результаті управління ризиком. Джерело ризику – чинники (явища, процеси), які визначають невизначеність результатів (конфліктність) діяльності. Інформаційна ситуація – певний ступінь градації невизначеності знань про середовище, якими володіє суб'єкт ризику. Загальні принципи аналізу ризику: • збитки від ризику незалежні один від одного; • збитки одного вигляду необов'язково збільшують збитки іншого вигляду; • максимальні збитки не повинні перевищувати фінансових можливостей об'єктів. Послідовність аналізу: 1. Визначення чинників ризику. 2. Аналіз виявлених чинників. 3. Оцінювання видів ризику. 4. Визначення допустимого рівня ризику. 5. Аналіз окремих операцій управління ризиком. 6. Розробка заходів щодо зниження рівня ризику. Аналіз ризиків включає два взаємодоповнюючі види: якісний і кількісний. Аспекти якісного аналізу: • порівняльний аналіз аналогів і окремих результатів; • аналіз впливу ризикованих чинників на економічну ефективність економічного об'єкту. Ризикованим ситуаціям властиві наступні властивості: • наявність невизначеності; • наявність альтернатив і можливості вибору; • зацікавленість в результатах Прийняття рішень. Всі чинники, які обумовлюють ризик, діляться на об'єктивні і суб'єктивні. Кількісний аналіз ризику вимагає залучення кількісних критеріїв оцінки рівня ризику. Управління ризиком Якщо уникнути ризику неможливо, то управляти ризиком слід обов'язково, для цього необхідна система управління ризиком (СУР). Загальні підходи до управління ризиком: 1.Використовування всіх можливостей уникнути або понизити ступінь ризику. Особлива увага слідує приділяти аналізу величини втрат, особливо катастрофічних ризиків. 2.Контроль ризику, оптимізація ступеня ризику, зниження втрат. 3.Прийняття ризику за наявності його значення.
Принципи управління ризиком: 1.Недоцільно ризикувати великим ради меншого. 2.Не можна ризикувати більшим об'ємом, ніж дозволяють власні засоби. 3.Необхідно наперед передбачати можливі наслідки ризику. Методи зниження рівня ризику: 1.Організація інформованості про можливі ситуації ризику. 2.Лімітація витрат на операції. 3.Диверсифікація. 4.Створення резервів. 5.Страхування ризику. 6.Використовування гарантій і застав. Зміцнення положення і ефективності роботи підприємства (головний метод). Альтернативні способи рішення проблеми ризику: 1.Ухилення від ризику. 2.Попередження ризику (інформування). 3.Прийняття ризику. 4.Розподіл ризику. 5.Зовнішнє страхування ризику. 6.Внутрішні способи: лімітація. 7.Диверсифікація. 8.Створення резервів і запасів. 9.Отримання додаткової інформації. Одночасне використовування способів – суперпозиція. Лекція 2 Система кількісних оцінок Економічного ризику Питання лекції:
1. Загальні підходи до кількісної оцінки ризику в економіці. 2. Критерій ймовірності оцінки ризику. 3. Коефіцієнт, індекс і шкала ризику. 4. Нерівність Чебишева. 5. Коефіцієнт чутливості бета. 6. Часовий критерій ризику і його значення. 7. Часовова залежність дисперсного критерію ризику.
Література: [5, 6, 7, 8, 11, 12]
Середньоквадратичне відхилення втрат (СКВ). Оскільки рівень ризику асоціюється із ступенем відхилення можливих результатів від їх розрахункового значення (m), то для вимірювання ризику можна використовувати статистичний показник розсіювання випадкової величини – дисперсію (D). Використовуються такі показники: СКВ (σ) варіація (V). При цьому:
Чим більше СКВ, тим вище ризик. На величину СКВ впливають одиниці вимірювання, тому для порівняння різномасштабних проектів використовується варіація. Але СКВ і варіація – це усереднені оцінки, які можуть привести до відносин в гіршу сторону, особливо при асиметричних розподілах, крім того рідкісний по ймовірності результат може означати катастрофу. Тому існує необхідність вдосконалення кількісних показників ризику.
Крива ризику. Зони ризику. При аналізі ризикованої часто виникає задача - виділення окремих зон і зображення кривих, що характеризують ризик. Частіше всього виділяють 4 характеристики зони ризику: 1.Безризикова зона – результат діяльності більше розрахункового прибутку (РП), втрат немає; 2.Зона допустимого ризику – втрати не перевищують розрахунковий прибуток (РП); 3.Зона критичного ризику – втрати знаходяться в межах розрахункової виручки (РВ); 4.Зона катастрофічного ризику – збитки вищі за розрахункову виручку, але нижчі за майновий стан (ринкової вартості) підприємства (МС). За межами четвертої зони може знаходитися тільки зона банкрутства економічного об'єкту, що означає катастрофу.
Крива ризику зображає ці залежності і може бути побудована двома способами: а) інтервальний спосіб; б) кумулятивний спосіб. При інтервальному способі визначають ймовірність попадання втрат Пj в конкретний інтервал: Рбез = Р (Пj ≤ 0); Рдоп = Р (0 < Пj ≤ РП); Ркрит = Р (РП < Пj ≤ РВ); Ркат = Р (РВ< Пj ≤ МС).
РВ – розрахункова виручка на об'єкті; МС – майновий стан об'єкту ризику. При кумулятивному способі (W) визначається ймовірність неперевищення втрат граничного значення: Wбез = Р (Пj < РП); Wдоп = Р(Пj ≥ РП) = 1- Wбез; Wкрит= Р(Пj ≥ РВ); Wкат = Р(Пj ≥ МС).
Рекомендується [3,10] витримувати співвідношення: Wдоп < 0,1; Wкат < 0,001; Wкрит ≤ 0,01.
Крива ризику має вигляд:
Рис.2.1. Крива ризику. Можна також використовувати функцію густини розподілу ймовірності збитків f(x):
Заштрихована площа характеризує катастрофічний ризик.
Рис.2.2. Розподіл ймовірності ризику.
Неравенство Чебишева Ймовірність настання ризикової події, математичне очікування, дисперсія (варіація) можливої втрати характеризують ризик з різних точок зору, але всі ці характеристики зв'язані між собою нерівністю Чебишева, яка формулюється таким чином: "Як би ні було позитивне число α, ймовірність того, що величина Х відхиляється від свого математичного очікування не менше ніж на α, обмежена зверху величиною
де Dх – дисперсія величини х. У разі, коли величина Х безперервна, нерівність Чебишева визначається аналогічним чином:
Вважаючи в нерівності Чебишева, маємо:
Ймовірність того, що відхилення випадкової величини від її математичного очікування вийде за межі трьох СКВ, не може бути більше Нерівність Чебишева дає тільки верхню межу даної ймовірності. Вище за цю межу ймовірність не може бути. Наприклад, для нормального закону ця ймовірність рівна 0,003.
5.Коефіцієнт чутливості Бета β Аналіз і оцінка співвідношення ризику і доходу (збитків) виконує важливу роль при інвестуванні і покупці цінних паперів. При цьому як основний показник систематичного фінансового ризику використовується коефіцієнт чутливості β. Систематичний ризик акції пов'язаний з вірогідністю подій, які впливають на фондовий ринок в цілому, і його не можна уникнути шляхом диверсифікації портфеля цінних паперів. Показник β характеризує мінливість доходів за певну акцію щодо доходів в середньому по ринку повністю диверсифікованого портфеля, яким в ідеальному випадку є весь ринок цінних паперів. Вважають, що систематичний ризик для "середньої" акції, динаміка доходів по якій співпадає з динамікою ринку цінних паперів, в цілому рівна 1. Величина β³ – коефіцієнт систематичного ризику і-го активу (акції). Вона характеризує густину зв'язку між біржовим курсом акцій і-ой компанії і загальним станом ринку і визначається формулою:
Cov(Ri, Rm) – коваріація випадкових величин Ri и Rm;
де Ri - прибутковість і-го капітального активу (акції); Rm- загальноринковий середній рівень доходу; σ(Ri), σ(Rm) – середньоквадратичне відхилення відповідно і-го капітального активу і загальноринкової прибутковості; Cov(Ri, Rm) m) – коваріація прибутковості і-го активу і прибутковості ринку;ρ(Ri, Rm) – коефіцієнт кореляції прибутковості і-х цінних паперів і ринкової ставки доходу. Значення β регулярно публікуються в західній фінансовій періодиці; σ використовується для оцінки якості інвестиційного проекту (ІП), зокрема, наскільки очікуваний дохід компенсує ризиковану внесків в певний вид цінних паперів. Розрахунком β займаються консалтингові фірми. Показник β =1,35 свідчить про підвищену ризиковану фірми. Якщо фондовий індекс підвищиться на 20%, то у даної компанії – на 27%.
І з урахуванням ризику
Питання лекції: 1.Загальні положення за поданням фінансових ресурсів. 2.Властивості аддитивності в операціях з фінансовими ресурсами. 3.Схеми (моделі) визначення ефективності використовування фінансових ресурсів. 4.Оптимізація розподілу інвестицій (модель В). 5.Динамічна модель розподілу ресурсів (модель Д). 6.Визначення ефективності інвестування.
Література: [2, 3, 8].
Оптимізація розподілу інвестицій (модель В) Модель В. Найадекватніше описує ситуацію оптимального розподілу інвестиційних (кредитних) ресурсів між замовниками. Такий же розподіл використовується при розподілі виробничих, фінансових і трудових ресурсів в державному масштабі і на нижчих рівнях управління. Розподільні алгоритми цього вигляду знаходять застосування при розподілі інвестиційних ресурсів в процесах реструктуризації. Позначимо в моделі rj через р(рj= rj - ймовірність співзагублення ресурсу. Тоді модель перетвориться до вигляду:
Для вирішення задачі (4) використаємо метод функціональних рівнянь динамічного програмування і позначимо:
де Gj – мінімум функції, одержаної в результаті j-крокового процесу при виборі на кожному j- м кроці такого ресурсу xj, який забезпечить мінімум функції Gj. В даному випадку має місце система рекурентних рівнянь:
У системі рівнянь (5):
Після визначення послідовності функцій gj при заданому значенні R в зворотному порядку визначаємо:
…………….
……………..
Визначимо послідовно вирази функцій gj.
Звичними методами визначимо екстремальне значення х2, для чого знаходимо:
Обчислимо другу похідну:
Знак другої похідної указує на наявність мінімуму g2. З виразу (5) знаходимо значення х2, що оптимізує g2:
Аналогічним методом, дозволяючи систему (5), знаходимо:
Остаточно визначаємо для системи (5) рішення у вигляді:
Модель С. Привикористовуванні цієї моделі рішення xj = 0 виглядають очевидними, тому необхідні додаткові обмеження xj ≥ xjmin, які і визначають рішення.
Динамічна модель розподілу ресурсів (модель Д) Модель Д. Ценайбільш широко використовувана модель розподілу банківських ресурсів, оскільки в ній відображається вимога заощадження ресурсів, а дохід прямо пропорційний їх об'єму. Розподіл банківських ресурсів відбувається при виконанні операцій в часі. При цьому набувають актуальність динамічні розподільні моделі, що враховують ризик. Постановка такої задачі має вигляд:
де хj - об'єм виділеного ресурсу; Nj – питомий дохід на одиницю ресурсу (процентна ставка); φj(tj) – функція ризику втрати доходу за час tj. В даному випадку Fj характеризує дохід від вкладення j-го активу. Якщо розв'язується задача розподілу ресурсів між М активами, то постановка задачі прийме вигляд: Визначити хj, що максимізують загальний дохід F, причому
При визначенні часовового критерію ризику показано, що:
Визначимо першу похідну
Рішення рівняння (7) має вигляд:
Рішення х(1) не має сенсу, тому приймаємо х(2).
Розглянемо
і в точці екстремуму маємо максимум. Результати розрахунку хopt при різних значеннях tj λj(Pj) приведені в табл.4.1.
Таблиця 4.1. Розрахунок оптимального хj
У табл.4.1. час вимірюється в роках, а значення х вимірюється в одиницях, щодо яких визначається ризик Pj і значення Nj. Аналіз результатів, приведених в табл.1, дозволяє зробити висновки: 1.При визначенні величини ресурсу, видаваного як кредит, існує його оптимальне значення (табл.4.1.). 2.Величина кредиту, що виділяється, в значній мірі визначається рівнем ризику, особливо при великих часовових інтервалах. 3.Величина оптимального об'єму кредиту обернено пропорційна часу, на яке він видається. Досліджуємо розподіл ресурсів між об'єктами, спочатку розглянемо випадки М = 2, тоді j = 1,2. При цьому з (6) слідує:
Оскільки х1+ х2 ≤ R, замість х1 використовуємо позначення х, а замість х2 підставимо у формулу (8) R-х, в результаті одержимо:
Знайдемо екстремальне рішення для (9), для чого визначимо:
У явному вигляді знайти значення коріння рівняння (10) не вдається, тому визначимо характер рішення (10). Виберемо довільну крапку
отже, функція Для з'ясування характеру функції F1,2(x) побудуємо графік залежності F1,2(x) за даними, приведеними в табл. 4.2.
Таблиця 4.2. Значення параметрів функції.
Рис.4.1. Графік залежності F1,2(x) = f (x) Аналіз графіків залежності F1,2(x) дозволяє зробити висновки: 1.Варіант 1 показує, що оптимальний розподіл допускається при х = 16-18, коли основний ресурс вкладається в менш прибутковий (N1) об'єкт, але менш ризикований. 2.Варіант 2 показує корисність диверсифікації, коли частина ресурсу (х = 4-6) прямує в менш прибутковий об'єкт при однаковому рівні ризику. 3.Порівняння варіантів 1 і 2 також підтверджує корисність диверсифікації: загальний дохід максимізується при розподілі ресурсу між більш прибутковим (R-x) і менш прибутковим, оскільки при цьому відбувається розподіл ризику. 4.Найбільше значення на розподіл ресурсу надає не значення Nj, а рівень ризику (Pj) і час надання кредиту. Дослідження (формули (6), (9) і рис.4.1.) показали залежність об'єму виділення ресурсу від значень Pj і tj. Але результати розподілу ресурсів по об'єктах можуть не співпадати з індивідуально певними значеннями (диверсифікація). Наприклад, на графіках рис.4.1. при індивідуальному розрахунку хopt = 19,5; (R-x)opt = 3,5. Одночасне при сумісному розрахунку хopt = 16; (R-x)opt = 4 для першого варіанту. Для другого варіанту хopt = 6; (R-x)opt = 14.
Теорія корисності Корисність означає ступінь задоволення суб'єкта від виконання деякої дії. Корисність – це використовуваний критерій в теорії Прийняття рішень. Найзагальніший підхід при встановленні ступеня оцінки ризику полягає у введенні функції корисності (Ф.П.). Будь-яке рішення (дія) в умовах ризику не може бути однокритерійним. Будь-який критерій (дохід, втрати, ймовірність отримання доходу, СКВ отримання доходу) сприймається через призму ризику, а ризик – слідство невизначеності. Корисність і дохід не тотожні, але їх взаємовідношення прозоре: корисність прямо пропорційна доходу. Зв'язок же корисності з ризиком не так очевидний, тим паче, що: а) корисність прямо пропорційна доходу; б) дохід і рівень ризику зв'язані (Марковіц): чим більше дохід, тим менше ризик і навпаки. Ставиться в цих умовах задача: як сумістити оцінку корисності і рівень ризику? Не дивлячись на наявність взаємозв'язку, корисність і дохід не тотожні, їх співвідношення сильно залежить від ситуації. Для оцінки ступеня корисності вводяться різні поняття, зокрема саме поняття " полезность",например, " пріоритетність". При оцінці корисності часто використовуються нерядкові оцінки: 1) більш пріоритетне, ніж - > 2) байдуже - ~ 3) не гірше, ніж - ≥ Поняття корисності носить, як правило, суб'єктивний характер. Для різних суб'єктів одне і теж кількість товару або чого-небудь ще може мати різну корисність. У теорії корисності важливе значення має поняття " гранична корисність"- додаткова корисність при споживанні додаткової кількості товару. Залежить від попередньої кількості. Приклад: перші 5 плиток шоколаду мають більшу корисність, ніж 5 подальших плиток і т.д. Граничну корисність звичайно вимірюють при отриманні додаткової одиниці товару (блага).
2.Корисність по Нейману Корисність по Нейману оцінюється за допомогою лотереї, яка визначає, одержати х* з вірогідністю (1-р) або х* з вірогідністю р. Величини виграшу в лотерею х* і х* вибираються так, що что х*≡ х, х*< х, для всіх х х* - найпріоритетніше значення виграшу. Експерту пропонують вибір: одержати суму х або виграш в лотерею. Під лотереєю розуміється ситуація виграшу х* з вірогідністю р або х* з вірогідністю (1-р). Лотерея L (х*, р(х), х*). Значення р змінюються до тих пір, поки значення х і виграш в лотерею приблизно порівняються. Очікуваний виграш в лотерею L (лотерея має N виграшів, І – корисність):
Справедлива головна формула теорії очікуваної корисності:
Поняття " певного еквівалента" лотереї L є одним з основних при розгляді різних характеристик ризику і їх взаємозв'язку з функціями корисності. Певний еквівалент лотереї L – це гарантована сума, отримання якої еквівалентне участі в лотереї, тобто
Якщо можливі виграші описуються щільністю розподілу φ(υ), то очікуваний виграш в лотереї рівний:
а певний еквівалент
Певний еквівалент – суб'єктивна оцінка лотереї на основі оцінок очікуваних результатів. Приклади функції корисності (певного еквівалента). 1.Зростаюча функція для суб'єкта, байдужого до ризику: І(х)= а + вх; у > 0. 2. Зростаюча функція для суб'єкта, не схильного до ризику: І(х)= log(x + у), х > -в. 3.Зростаюча функція з несхильністю до ризику: И(х) = а – ве-сх, в > 0, х ≥ 0. 4. Зростаюча функція з схильністю до ризику: И(х) = а – ве-сх, в > 0, х ≥ 0.
По своїй фізичній суті премія за ризик (надбавка за ризик) – це сума (у одиницях вимірювання критерію х – виграш або збиток), якої суб'єкт управління ризиком згоден пожертвувати з середнього виграшу, щоб уникнути ризику (платня за ризик), пов'язаного з лотереєю. 3.Відношення до ризику суб'єкта управління ризиком Суб'єкта називають несхильним до ризику, якщо для нього пріоритетніше одержати гарантовано очікуваний виграш в лотерею, ніж брати в ній участь. Оскільки корисність лотереї співпадає з математичним очікуванням корисності і випадкових результатів, та умова несхильності до ризику має вигляд:
де х – випадкова величина виграшу, залежна від результату ω. Різниця між очікуваним виграшем і певним еквівалентом
Страховою сумою (СС) називають величину певного еквівалента з протилежним знаком:
Умови відношення суб'єкта управління ризиком до ризику: 1) 2) 3) де
Оскільки для байдужості до ризику
і вони співпадають, то функція І(х) – лінійна. Якщо особа нейтральна до ризику – функція корисності лінійна. Для особи, несхильної до ризику, привабливішим є отримання гарантованої суми (середній виграш лотереї), тобто
Функція, що задовольняє цьому рівнянню, називається увігнутою (опуклої вгору). Особа, несхильна до ризику, має опуклу вгору функцію корисності.
Рис.5.1. Залежність ризику для особи, несхильної до ризику.
Для особи, схильної до ризику, виконується умови:
Цій умові задовольняє опукла (опукла вниз) функція. Особа, схильна до ризику, має опуклу вниз функцію корисності.
Рис.5.2. Залежність ризику для особи, схильної до ризику.
Премія за ризик Певний еквівалент (позначимо його через d) може брати участь у визначенні премії за ризик. Премія за ризик (r) – різниця між очікуваним виграшем і певним еквівалентом:
Премія r > 0 - при несхильності до ризику і r < 0 - при схильності до ризику. Розглянемо лотерею В цьому випадку можна записати: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |



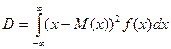 для безперервної величини або
для безперервної величини або при а? х? у.
при а? х? у.



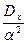 :
:


 .
.
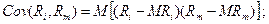

 (4)
(4)
 (5)
(5)






 (5)
(5)



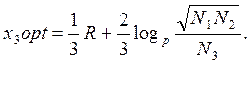



 при
при 

 . (6)
. (6)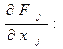
 . (7)
. (7)
 .
.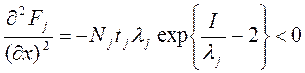

 (8)
(8) (9)
(9) (10)
(10) і розглянемо значення
і розглянемо значення 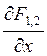 в крапках, де - мала величина. З рівняння (10) безпосередньо визначаємо:
в крапках, де - мала величина. З рівняння (10) безпосередньо визначаємо: ,
, - зростаюча, що дає можливість припустити існування максимуму.
- зростаюча, що дає можливість припустити існування максимуму. X
Варіанти
X
Варіанти





 Х,, тобто х* - якнайменше пріоритетне значення виграшу;
Х,, тобто х* - якнайменше пріоритетне значення виграшу;

 - корисність ансамблю результатів співпадає з математичним очікуванням корисності результатів.
- корисність ансамблю результатів співпадає з математичним очікуванням корисності результатів.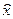 ~ L. Значення
~ L. Значення  або
або 



 називають премією за ризик.
називають премією за ризик.
 - несхильність до ризику;
- несхильність до ризику; - схильність до ризику;
- схильність до ризику; - байдужість до ризику,
- байдужість до ризику,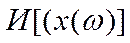 - функція корисності результату ω.
- функція корисності результату ω.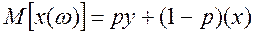 (очікуваний виграш),
(очікуваний виграш),








