
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості аддитивності в операціях з фінансовими ресурсамиСодержание книги
Поиск на нашем сайте
Ресурси, виручка, витрати і можливі втрати банківської діяльності вимірюються в грошовому виразі. Ця обставина визначає аддитивність моделей банківських операцій. Загальний вид функціонала, що визначає ефективність виконання проекту Fj, представляється виразом:
Природно вважати об'єкти вкладення ресурсів незалежними між собою, при цьому загальна очікувана ефективність від вкладення R одиниць ресурсів в М об'єктів визначається сумою:
При виконанні відношення (1) функція F задовольняє властивостям аддитивності і для визначення оптимального значення F може бути використаний апарат динамічного програмування, зокрема, метод функціональних рівнянь [2]. Для цього складається система функціональних рівнянь, що максимізують F:

Після побудови системи (2) при заданому значенні R в зворотному порядку визначаються оптимальні рішення:
……………..
………………
З метою економії часу на розрахунки нумерацію j слід вибирати так, щоб значення Nj із зростанням j зменшувалися (не зростали). При цьому, після рішення xj = 0 подальші рішення (xj+1, xj+2… xjм) будуть також нульовими. Якщо при побудові системи (2) не вдається одержати результати в аналітичному вигляді, то функції xj визначаються табуляцією. Для вирішення прикладних задач з використанням моделей (1) -(2) необхідно визначити вид виразу (1) для функції Fj. Для цієї мети необхідно розглядати реальні схеми визначення ефективності реалізації проекту Fj із змінними xj, Nj, tj и φj(t). З цією метою розглянемо моделі А, В, С, Д, що мають прикладну інтерпретацію.
Схеми (моделі) визначення ефективності використовування фінансових ресурсів Модель А. Передбачається, що ресурс xj інвестується на виконання проекту, дохід від реалізації якого пропорційний xj. Враховується ймовірність ризику втрати ресурсу rj і не враховується його залежність від часу φj(t). Тоді:
Модель В. Ресурс xj інвестується на виконання проекту, дохід пропорційний xj і Nj. За час виконання проекту кожна одиниця ресурсу втрачається (або витрачається) з вірогідністю rj. Проект завершується успішно, якщо до його завершення зберігається, хоча б одна одиниця ресурсу. В цьому випадку:
Модель С. Ресурс xj інвестується на виконання проекту, дохід пропорційний Nj. Кожна одиниця ресурсу схильна до ризику втрати з вірогідністю rj. Проект виконується успішно, якщо весь ресурс за час виконання проекту зберігається в повному об'ємі. В цьому випадку:
Модель Д. Ресурс інвестується на виконання проекту. Дохід пропорційний Nj і xj. Кожна одиниця ресурсу може бути втрачена з вірогідністю rj. Максимізовується дохід, пропорційний Nj і частини ресурсу xj, яка зберігається. В цьому випадку:
У всіх розглянутих моделях час виконання проекту не розглядається і вважається фіксованим. Модель Д найбільшою мірою адекватна опису операції банківського кредитування. Найкритичнішим в моделі до часу tj є рівень ризику rj(t) = φj(t). Часовова функція φ(t) однозначно визначається часом виконання проекту, вірогідністю втрати одиниці ресурсу у встановлений період часу (наприклад, 1год) і дає можливість вводити в модель часовий параметр t. Розглянемо використовування представлених моделей. Модель А. Для визначення значень xj, що максимізують F відповідно до (1), слідує додатково вводити в модель обмеження xj ≤ Rj. При цьому може бути використаний алгоритм: 1.Формується масив значень Nj(1- φj) і сортується по убуванню; 2.Для відсортованого масиву виконується моніторинг по j і на кожному кроці моніторингу визначається rj з співвідношення:
3. Моніторинг припиняється при виконанні умови:
4.Рішення має вигляд:
Оптимізація розподілу інвестицій (модель В) Модель В. Найадекватніше описує ситуацію оптимального розподілу інвестиційних (кредитних) ресурсів між замовниками. Такий же розподіл використовується при розподілі виробничих, фінансових і трудових ресурсів в державному масштабі і на нижчих рівнях управління. Розподільні алгоритми цього вигляду знаходять застосування при розподілі інвестиційних ресурсів в процесах реструктуризації. Позначимо в моделі rj через р(рj= rj - ймовірність співзагублення ресурсу. Тоді модель перетвориться до вигляду:
Для вирішення задачі (4) використаємо метод функціональних рівнянь динамічного програмування і позначимо:
де Gj – мінімум функції, одержаної в результаті j-крокового процесу при виборі на кожному j- м кроці такого ресурсу xj, який забезпечить мінімум функції Gj. В даному випадку має місце система рекурентних рівнянь:
У системі рівнянь (5):
Після визначення послідовності функцій gj при заданому значенні R в зворотному порядку визначаємо:
…………….
……………..
Визначимо послідовно вирази функцій gj.
Звичними методами визначимо екстремальне значення х2, для чого знаходимо:
Обчислимо другу похідну:
Знак другої похідної указує на наявність мінімуму g2. З виразу (5) знаходимо значення х2, що оптимізує g2:
Аналогічним методом, дозволяючи систему (5), знаходимо:
Остаточно визначаємо для системи (5) рішення у вигляді:
Модель С. Привикористовуванні цієї моделі рішення xj = 0 виглядають очевидними, тому необхідні додаткові обмеження xj ≥ xjmin, які і визначають рішення.
Динамічна модель розподілу ресурсів (модель Д) Модель Д. Ценайбільш широко використовувана модель розподілу банківських ресурсів, оскільки в ній відображається вимога заощадження ресурсів, а дохід прямо пропорційний їх об'єму. Розподіл банківських ресурсів відбувається при виконанні операцій в часі. При цьому набувають актуальність динамічні розподільні моделі, що враховують ризик. Постановка такої задачі має вигляд:
де хj - об'єм виділеного ресурсу; Nj – питомий дохід на одиницю ресурсу (процентна ставка); φj(tj) – функція ризику втрати доходу за час tj. В даному випадку Fj характеризує дохід від вкладення j-го активу. Якщо розв'язується задача розподілу ресурсів між М активами, то постановка задачі прийме вигляд: Визначити хj, що максимізують загальний дохід F, причому
При визначенні часовового критерію ризику показано, що:
Визначимо першу похідну
Рішення рівняння (7) має вигляд:
Рішення х(1) не має сенсу, тому приймаємо х(2).
Розглянемо
і в точці екстремуму маємо максимум. Результати розрахунку хopt при різних значеннях tj λj(Pj) приведені в табл.4.1.
Таблиця 4.1. Розрахунок оптимального хj
У табл.4.1. час вимірюється в роках, а значення х вимірюється в одиницях, щодо яких визначається ризик Pj і значення Nj. Аналіз результатів, приведених в табл.1, дозволяє зробити висновки: 1.При визначенні величини ресурсу, видаваного як кредит, існує його оптимальне значення (табл.4.1.). 2.Величина кредиту, що виділяється, в значній мірі визначається рівнем ризику, особливо при великих часовових інтервалах. 3.Величина оптимального об'єму кредиту обернено пропорційна часу, на яке він видається. Досліджуємо розподіл ресурсів між об'єктами, спочатку розглянемо випадки М = 2, тоді j = 1,2. При цьому з (6) слідує:
Оскільки х1+ х2 ≤ R, замість х1 використовуємо позначення х, а замість х2 підставимо у формулу (8) R-х, в результаті одержимо:
Знайдемо екстремальне рішення для (9), для чого визначимо:
У явному вигляді знайти значення коріння рівняння (10) не вдається, тому визначимо характер рішення (10). Виберемо довільну крапку
отже, функція Для з'ясування характеру функції F1,2(x) побудуємо графік залежності F1,2(x) за даними, приведеними в табл. 4.2.
Таблиця 4.2. Значення параметрів функції.
Рис.4.1. Графік залежності F1,2(x) = f (x) Аналіз графіків залежності F1,2(x) дозволяє зробити висновки: 1.Варіант 1 показує, що оптимальний розподіл допускається при х = 16-18, коли основний ресурс вкладається в менш прибутковий (N1) об'єкт, але менш ризикований. 2.Варіант 2 показує корисність диверсифікації, коли частина ресурсу (х = 4-6) прямує в менш прибутковий об'єкт при однаковому рівні ризику. 3.Порівняння варіантів 1 і 2 також підтверджує корисність диверсифікації: загальний дохід максимізується при розподілі ресурсу між більш прибутковим (R-x) і менш прибутковим, оскільки при цьому відбувається розподіл ризику. 4.Найбільше значення на розподіл ресурсу надає не значення Nj, а рівень ризику (Pj) і час надання кредиту. Дослідження (формули (6), (9) і рис.4.1.) показали залежність об'єму виділення ресурсу від значень Pj і tj. Але результати розподілу ресурсів по об'єктах можуть не співпадати з індивідуально певними значеннями (диверсифікація). Наприклад, на графіках рис.4.1. при індивідуальному розрахунку хopt = 19,5; (R-x)opt = 3,5. Одночасне при сумісному розрахунку хopt = 16; (R-x)opt = 4 для першого варіанту. Для другого варіанту хopt = 6; (R-x)opt = 14.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.116.142 (0.009 с.) |


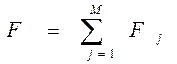 при
при  (1)
(1)



 (3)
(3)





 (4)
(4)
 (5)
(5)






 (5)
(5)



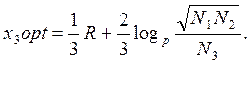



 при
при 

 . (6)
. (6)
 . (7)
. (7)
 .
.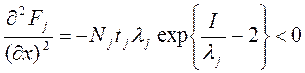

 (8)
(8) (9)
(9) (10)
(10) і розглянемо значення
і розглянемо значення 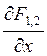 в крапках, де - мала величина. З рівняння (10) безпосередньо визначаємо:
в крапках, де - мала величина. З рівняння (10) безпосередньо визначаємо: ,
, - зростаюча, що дає можливість припустити існування максимуму.
- зростаюча, що дає можливість припустити існування максимуму. X
Варіанти
X
Варіанти








