Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прийняття економічних рішень в умовах ризикуСодержание книги
Поиск на нашем сайте
Питання лекції: 1.Теоретико-ігрова постановка. 2.Інформаційна ситуація (аналіз середовища). 3.Критерій Прийняття рішень (вирішальне правило). 4.Критерії Прийняття рішення в ситуації з антагоністичними інтересами (І5). 5.Прийняття рішення в умовах конфлікту.
Література: [8].
Теоретико-ігрова постановка Ситуації Прийняття рішень часто виникають тоді, коли з кожним варіантом рішення Ситуація Прийняття рішень складається на основі дозволу ігрової взаємодії двох гравців: " середовище – ОПР". Задачу пропонується вирішити в 2 етапи: 1) На першому етапі складається матриця результатів рішення: розраховуються очікувані результати Хik по кожному варіанту рішення i для кожного стану середовища до. Створюється матриця (функціонал) оцінювання.
2) На другому етапі формується правило (критерій) вибору рішення. Критерії вибираються відповідно до гіпотез, прийнятих ОПР щодо середовища. Для дозволу даної ситуації і Прийняття рішення може бути використана теоретико-ігрова модель ситуації. Ситуація розглядається як гра двох гравців: " ОПР – середовище". Основними поняттям моделі є: 1) Объект управління і множину управлінських рішень ri. Правильність вибору множинуі рішень характеризує наявність ризику. 2) Субъект управління – ОПР. Формує множину рішень. 3) Економічне середовище (господарське середовище), стан середовища. Ризик у визначенні стану середовища і опису множинуі станів (виконує ОПР). 4) Функціональне оцінювання. При його визначенні ОПР приймає ризик за правильність потроєння функціонала. 5) Критерій (правило) Прийняття рішення. Виконує ОПР відповідно до інформації про стан середовища. 2.Інформаційна ситуація (аналіз середовища) Під інформаційною ситуацією розуміється певний ступінь градації невизначеності у визначенні станів середовища у момент Прийняття рішення. Пропонується наступний класифікатор інформаційних ситуацій (стан невизначеності середовища): I1 – перша інформаційна ситуація. Задані елементи множини станів I2 – те ж, але невідомі параметри закону розподілу. I3 – (третя інформаційна ситуація). Те ж, але невідомі закони розподілу. Задані апріорні відомості про можливі закони. I4 – розподіл ймовірності Sk не визначено. I5 – антагонізм середовища і ОПР (конфлікт інтересів). I6 – проміжна ситуація між I1 і I5. Кожна інформаційна ситуація характеризується функціоналом оцінювання і вирішальним правилом або критерієм вибору рішень (сукупністю критеріїв). ОПР має в своєму розпорядженні функціонал оцінювання Творча складова Прийняття рішення в умовах ризику має вирішальне значення і складається з наступних основних кроків: 1.Формування множини рішень 2.Визначення і формалізація основних показників ефективності і корисності, які входять у функціонал оцінювання 3.Визначення інформаційної ситуації, яка визначає стратегію поведінки економічного середовища. 4.Вибір критерію Прийняття рішення для даної інформаційної ситуації. 5.Прийняття оптимального рішення по вибраному критерію. Формальна складова процесу Прийняття рішення в умовах ризику і невизначеності полягає в проведенні розрахунків показників, що входять у визначення функціонала оцінювання, і розрахунків по вибору оптимального рішення. Наприклад для I1 найбільш вживаються критерії: Байеса, модальний, мінімальної дисперсії; для I4 – Джейнса, Лапласа і др.; для I5 – Вальда, Севіджа і др.; для I6 – Гурвіца, Ходжеса-Лемана і ін. Вважається, що функціонал оцінювання F має позитивний характер, якщо прагнуть досягти Функціонал ризику в ігровій моделі: Хай 1)
3) Для
3.Критерії Прийняття рішень (вирішальні правила) Критерій Байеса – максимізація математичного очікування функціонала оцінювання для f+ - критерій середніх витрат:
В+-байесово значення функціонала оцінювання. Найпоширеніший критерій в I1, тісно пов'язаний з аксіомами теорії корисності Неймана-Моргенштерна. Для
Критерій мінімуму дисперсії функціонала оцінювання. Суть критерію – мінімізація ризику – розкид розподілу випадкової величини функціонала оцінювання:
Недолік цього критерію у тому, що рішення може не співпадати з Байесовим рішенням. Критерії Прийняття рішення в ситуації I4. Критерій Бернулі-Лапласа. У ситуації I4 нічого невідоме про стан середовища, тому доцільно вважати їх рівноімовірними.
де:
Пріоритетність рішень визначається тільки значенням fik. Принцип максимуму Гиббса-Джейнса. Відповідно до цього принципу найхарактернішою вірогідністю станів середовища є ті, які максимізують невизначеність (ентропію) станів середовища. З теорії інформації відомо, що максимізація ентропії наступає при рівноімовірних станах. Звідси слідує збіг принципу Гиббса-Джейнса з критеріями Бернуллі-Лапласа. 4.Критерії Прийняття рішень в ситуації з антогоністічеськімі інтересами (I5) У цій ситуації середовище не є пасивним і слід розраховувати на її активну протидію (зниження позитивних результатів рішення). Критерій Вальда (критерій песиміста, максиміна). Вибирається той варіант рішення, який забезпечує якнайкращий результат при найгіршому стані середовища. Вирішальне правило:
Критерій мінімального ризику Севіджа. Критерій запропонований в 1951 році і є основним, задовольняючим принципу мінімакса. У критерії Севіджа функціонал оцінювання виражається у формі ризику F=F-
Обмеження
По критерію Севіджа вибирається той варіант, який забезпечує мінімальний з максимальних "жалів". "Жаль " показує наскільки варіант рішення при даному стані середовища гірший за результат при якнайкращому її стані. Вирішальне правило:
Якщо про стан середовища нічого невідоме, то вибирають критерій Лапласа і Гурвіца. Критерії Вальда і Севіджа песимістичні в тому значенні, що виходять із стану середовища, які є гарантованими і безризиковими. Але можна спробувати оцінити поведінку середовища, яка буде кращою для ОПР і виходити з комбінації якнайкращого і якнайгіршого. Такий підхід до Прийняття рішення відомий як критерій "песимізму-оптимізму" був вперше запропонований Гурвіцем. По критерію Гурвіца використовується коефіцієнт довіри β (0 ≤ β ≤ 1), він є оцінкою середовища ОПР. Вирішальне правило:
При β = 0 критерій Гурвіца співпадає з критерієм Вальда.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.83.202 (0.009 с.) |

 пов'язано декілька можливих результатів
пов'язано декілька можливих результатів  і ймовірність цих результатів
і ймовірність цих результатів  залежать від стану зовнішнього середовища Sk. Ймовірність знаходження середовища
залежать від стану зовнішнього середовища Sk. Ймовірність знаходження середовища  в кожному із станів невідома і ОПР дає їм оцінки.
в кожному із станів невідома і ОПР дає їм оцінки.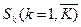 і законом розподілу ймовірності цих станів із заданими параметрами.
і законом розподілу ймовірності цих станів із заданими параметрами. , який характеризує виграш або програш під час вибору рішення ri,, якщо середовище знаходитиметься в стані Sk.
, який характеризує виграш або програш під час вибору рішення ri,, якщо середовище знаходитиметься в стані Sk. і множини станів середовища
і множини станів середовища 
 і записують
і записують  Для негативного характеру прагнуть досягти
Для негативного характеру прагнуть досягти  і запис
і запис 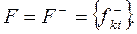
 Функція ризику визначається у вигляді:
Функція ризику визначається у вигляді: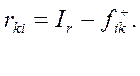
 Функція ризику
Функція ризику 
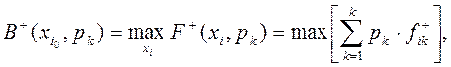






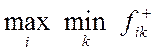


 для всіх хі.
для всіх хі.