
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про ірраціональне число і множину дійсних чисел. Методика викладання тотожних перетворень ірраціональних виразів.Содержание книги
Поиск на нашем сайте
За чинною програмою треба вивчати ірраціональні числа і множину дійсних чисел у 8 клас на доступному рівні за короткий час, без багатьох означень і доведень або фактично на рівні уявлень. Тому мотивання і введення ірраціональних чисел можна здійснити таким методичним варіантом. На одиничному відрізку координатної прямої будується квадрат і ставеться за мету визначити довжину його діагоналей ОК, а відповідне число зобразити точкою Р на координатний прямій.Геометрично це виконується легко відкладанням циркулем відрізка ОК на координатній прямій.Однак виникає запитання: яким чином виражається координата точки К. Щоб з’ясувати це, позначимо довжину відрізка ОК буквою х і побудуємо ще один квадрат, стороною якого є відрізок ОК. З рисунка видно, що площа квадрата вдвоє більша за площу одиничного квадрата. Одже, х2=2, оскільки площа одиничного квадрата дорівнює 1. Щоб визначити х,треба розв’язати одержане квадратичне рівняння. Геометричний спосіб розв’язання свідчить про те, що існують два корені цього рівняння. Квадрат кожного з них дорівнює 2. З попереднього матеріалу учні вже знають, що число, квадрат якого дорівнює 2, наз. Квадратним коренем. Арифметичний квадратний корінь позначається символом. Тому два корені рівняння х2=2 є не що інше як числа. Які це числа. Далі формується і доводиться методом від супротивного твердження: не існує раціонального числа, квадрат якого дорівнює 2. Отже, корені рівняння не належать до раціональних чисел, Звертається увага на те, що не є ірраціональними числа також. Такі числа називаються ірраціональними. (можна обчислити з якою завгодно к-тю десяткових знаків наближене значення числа, можна показати на калькуляторі) Ірраціональних чисел можна утворити безліч, якщо записувати неперіодичний десятковий дріб. Інакше і бути не може, бо тоді б вони були числа раціональні. Якщо множину раціональних чисел доповнити ірраціональними, то одержана множина називається множиною дійсних чисел і позначається буквою. У множині дійсних чисел виявилась можливою дія добування корення з раціональних чисел і деякі інші математичні операції.
Переважну більшість тотожних перетворень іррац. виразів виконують, користуючись теоремами про радикали (для додатних а, Ь) звичайно записують так: У 8 класі розглядають лише деякі з цих тотожностей до того ж тільки з квадратними коренями. Майже всі ці співвідношення доводять однаково, тому ми спинимось на доведенні першого з них для n = 2. Щоб довести при невід'ємних значеннях а, b тотожність піднесемо обидві частини цієї рівності до квадрата: Як бачимо, квадрати обох частин рівні, тому тотожність справедлива. Міркування було б правильне, коли б ми підкреслили, що обидві частини доводжуваної рівності – числа додатні, а перед цим довели таку лему: якщо квадрати додатних чисел рівні самі числа. Після доведення цієї тотожності учням ще раз треба нагадати що а, Ь — невід'ємні числа. З найхарактерніших помилок, що їх допускають учні в перетворенні ірраціон. виразів є неправильне винесення множників з-під знаку кореня і неправильне внесення множників під знак кореня. Учні вважають, що рівність а√в=√а2в справедлива при всіх числових значеннях а, зокрема і при відємних Розв’язати систему вправ 1) винесення мн-на за знак кореня, 2) внесення множника під знак кореня, 3) якщо знак кореня міститься в знаменику дробу, такий дріб можна замінити тотожнім йому дробом, знаменник якого не містить коренів, досить домножити члени дробу на відповідно підібраний вираз, такі перетворення наз. звільненням дробу від ірраціональності. 12. Рівняння та нерівності в основній школі і методика їх вивчення.Методика вивчення дробово-раціональних рівнянь та нерівностей. Метод інтервалів .
У школі поняття рівняння вводять досить рано, в 2-му класі. У 5 класі досить обмежитись таким означенням: “Рівність, яка містить невідоме число, наз рівнянням”. Розв’язувати найпростіші рівняння можна такими способами: 1. На основі залежностей між компонентами і результатами дій; 2. За властивостями рівностей; 3. За теоремами про рівносильність рівнянь; 4. Графічний спосіб. Найпростіші рівняння учні розв’язують вже в початкових класах. Тут вони або підбирають корені, або використовують залежності між компонентами і результатами дій. У 5-6 класах повторюють цей матеріал, уточняють, що означає розв’язати рівняння, що таке розв’язок або корінь. Коли учні ознайомляться з від’ємними числами, їм показують, що доданки можна переносити з однієї частини рівняння в іншу змінюючи при цьому їх знаки на протилежні, пояснюють цю властивість користуючись терезами. Термін рівносильні рівняння вперше з’являється 7 класі. Тут же формулюються і основні властивості: 1. Якщо до обох частин рівняння додати одне й те саме число, то дістанемо рівняння, рівносильне даному; 2. Якщо обидві частини рівняння помножити або поділити на одне й те саме число відмінне від нуля .3. Якщо в рівнянні перенести доданок з однієї частини в іншу, змінивши його знак на протилежний, то дістанемо рівняння, рівносильне даному. Розв’язують в 7 класі в основному лінійні рівняння з двома невідомими, його графік, систему лінійних рівнянь з 2-ма невідомими (ах+ву+с=0 в стандартному вигляді ах+ву=с)і способи їх розв’язування і такі, що легко розв’язуються розкладанням на множники. Треба відрізняти лінійні рів-ня від рівнянь першого степеня з однією зміною це рівняння виду ах+в=0, де а Вимоги до знань і умінь: знати означення лінійного, квадратного рів-ня і формулу його коренів; мати уявлення про дробово-раціональні рів-ня і знати способи їх розв’язування, розуміти зміст поняття системи двох рів-нь з 2-ма невідомими; вміти розв. лінійні, квадратні, дробово раціональні рівняння та їх системи. Дробово рац. рів-ня розв’язують скориставшись необхідною і достатньою умовою рівності нулю дробу: дріб дорівнює нулю тоді і тільки тоді коли чисельник =0, а знаменник не =0. Лінійні нерівності раніше вивчали в 7 кл. Про-те після того,як програма в 7 кл. була спрощена, цю тему було перенесено в 9 кл. Спочатку вивчають: числові нерівності: властивості числових нерівностей,їх доведення; лінійні нерівності і їх системи. При розв’язанні квадратних нерівностей використовують в-ть квадратичної функції. Звертаємо увагу на випадки коли а 0, тоді гілки параболи направлені в низ. Дробово-раціональні нерівності розв’язуються методом інтервалів.
Нерівності в математиці відіграють важливу роль. Із знаками > і < учні знайомляться ще в початковій школі. В 5-6-х класах їх використовують для порівняння чисел, розглядають подвійні нерівності, нерівності із знаками >=і <=. Окремий розділ “нерівності” вивчають в кінці 8-го або на початку 9-го класу. Тут учні ознайомлюються з властивостями числових нерівностей, вчаться розв’язувати нерівності з однією змінною і їх системи, застосовують нерівності до вивчення властивостей функцій і т. ін. Квадратичні, дробово-раціональні ті ін. нерівності вчаться розв’язувати в старших класах. Нерівності із змінними можна розв’язувати різними способами. Найраціональніший із них – на основі таких теорем про рівносильність нерівностей: 1. Якщо з однієї частини нерівності перенести в другу доданок з протилежним знаком, то дістанемо рівносильну їй нерівність. 2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то дістанемо рівносильну їй нерівність. 3 Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то дістанемо рівносильну їй нерівність. Загальні доведення цих теорем для учнів важкі, тому пропонується проілюструвати їх на прикладах.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 915; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.70.14 (0.012 с.) |

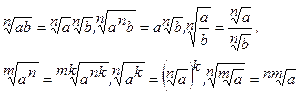 Вперше з ірраціональними виразами учні ознайомлюються в 8 кл. під час вивчення квадратних коренів. Вирази, які містять дію добування кореня зі змінної або виразу, який містить змінну наз. ірр.в. на цьму етапі навчання мають справу лише з ірр. в. які містять арифметичні квадратні корені. Вирази які містять корені будь- якого степеня вивчаються в курсі алгебри і поч..а. Як відомо, квадратний корінь, наприклад, з числа 25 має два значення: 5 і —5. Тому іноді пишуть: √25 = ±5. Такий запис неправильний, бо домовились під символом √25 розуміти тільки арифметичний корінь. Символ √ треба вводити не зразу після пояснення квадратного кореня, а пізніше, коли буде введено поняття арифметичного кореня. Тоді ж можна розглянути і тотожність (√а)2=|a| ця рівність справедлива при всіх значеннях а.
Вперше з ірраціональними виразами учні ознайомлюються в 8 кл. під час вивчення квадратних коренів. Вирази, які містять дію добування кореня зі змінної або виразу, який містить змінну наз. ірр.в. на цьму етапі навчання мають справу лише з ірр. в. які містять арифметичні квадратні корені. Вирази які містять корені будь- якого степеня вивчаються в курсі алгебри і поч..а. Як відомо, квадратний корінь, наприклад, з числа 25 має два значення: 5 і —5. Тому іноді пишуть: √25 = ±5. Такий запис неправильний, бо домовились під символом √25 розуміти тільки арифметичний корінь. Символ √ треба вводити не зразу після пояснення квадратного кореня, а пізніше, коли буде введено поняття арифметичного кореня. Тоді ж можна розглянути і тотожність (√а)2=|a| ця рівність справедлива при всіх значеннях а.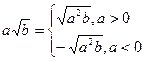
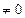 і в-довільне число, може мати безліч або зовсім не мати коренів. Розв’язуючи в 7-му кл. рівняння 2-го степеня розкладанням лівої частини рівняння на множники за умов рівності нулю правої частини. Систематичне вивчення квадратних рівнянь передбачене у 8-му кл., розв’язуються формулою коренів кв. рів-ня та способом виділення квадрата двочлена. В 9-му дробово-раціональні рівняння, які зводяться до квадратних, біквадратні рів-ня, симетричні, однорідні та системи рівнянь другого степеня а в 10-11-му вивчаються тригонометричні (найпростіші виду sinx=a, cosx=a, tgx=a), показникові і логарифмічні рівняння.
і в-довільне число, може мати безліч або зовсім не мати коренів. Розв’язуючи в 7-му кл. рівняння 2-го степеня розкладанням лівої частини рівняння на множники за умов рівності нулю правої частини. Систематичне вивчення квадратних рівнянь передбачене у 8-му кл., розв’язуються формулою коренів кв. рів-ня та способом виділення квадрата двочлена. В 9-му дробово-раціональні рівняння, які зводяться до квадратних, біквадратні рів-ня, симетричні, однорідні та системи рівнянь другого степеня а в 10-11-му вивчаються тригонометричні (найпростіші виду sinx=a, cosx=a, tgx=a), показникові і логарифмічні рівняння.


