
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття загального рівняння поверхні другого порядку.Содержание книги
Поиск на нашем сайте
План Поняття загального рівняння поверхні другого порядку. Перетин поверхні з прямою. Частинні випадки. Центр поверхні. Рівняння дотичної площини та нормалі. Поняття загального рівняння поверхні другого порядку. Розглянемо поверхню другого порядку
де Доданки Рівняння (1) називають загальним рівнянням поверхні другого порядку, оскільки з нього можна отримати будь-яке конкретне рівняння поверхні другого порядку. З поверхнями, рівняння яких є частинними випадками рівняння (1), ми уже зустрічалися в попередніх лекціях. Такими є сфера Оскільки рівняння (1) містить 10 коефіцієнтів, які визначаються з точністю до сталого множника, то поверхня другого порядку можна задавати не більше, ніж 9-ма точками. У деяких випадках їх кількість може бути меншою. Наприклад, сферу можна задати 4-ма точками, які їй належать. Меншою кількістю точок визначаються параболоїди, циліндри, конуси. Введемо в розгляд символи
а також
Вираз Найближчими нашими задачами буде дослідження властивостей поверхонь, заданих загальним рівнянням, вивчення особливостей їх розташування відносно системи координат, а також дослідження питання, скільки та які різні види поверхонь може визначати рівняння (1).
Центр поверхні. Хордою поверхні другого порядку назвемо відрізок, який сполучає дві її довільні точки. Якщо існує точка, в якій усі хорди, що проходять через неї, діляться пополам, то цю точку називають центром поверхні. Центр поверхні є її центром симетрії, оскільки разом із будь-якою точкою поверхні їй належить також точка, симетрична даній відносно центра. Розглянемо питання відшукання центра поверхні, заданої рівнянням (1). Як ми знаємо, умовою того, щоб точка
для довільного напрямку, який задається вектором
Існування та кількість розв’язків системи (4) залежить від її визначника
Якщо Якщо Приклад 1. Знайти центр поверхні, заданої рівнянням
Розв’язання. Складемо та розв’яжемо систему рівнянь
звідки
План Геометричне місце хорд, які в заданій точці діляться навпіл. План План Поняття загального рівняння поверхні другого порядку.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.171.83 (0.008 с.) |

 , задану рівнянням
, задану рівнянням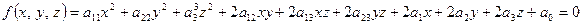 , (1)
, (1) – деякі дійсні числові коефіцієнти, причому коефіцієнти
– деякі дійсні числові коефіцієнти, причому коефіцієнти 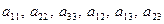 одночасно не дорівнюють нулю.
одночасно не дорівнюють нулю.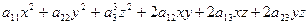 називають групою старших членів, або квадратичною формою, вираз
називають групою старших членів, або квадратичною формою, вираз  – лінійною частиною, число
– лінійною частиною, число  – вільним членом рівняння.
– вільним членом рівняння.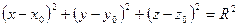 із центром у точці
із центром у точці  та радіусом
та радіусом  , еліпсоїд
, еліпсоїд  , одно- та двопорожнинні гіперболоїди
, одно- та двопорожнинні гіперболоїди  , еліптичний та гіперболічний параболоїди
, еліптичний та гіперболічний параболоїди 
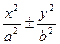 та інші. Природно виникає питання, чи всі можливі поверхні другого порядку ми розглянули? Приклад поверхні, яка задається рівнянням
та інші. Природно виникає питання, чи всі можливі поверхні другого порядку ми розглянули? Приклад поверхні, яка задається рівнянням  , показує, що ні. Справді, записавши дане рівняння у вигляді
, показує, що ні. Справді, записавши дане рівняння у вигляді  , бачимо, що його не задовольняють координати жодної точки. Можна навести і інші приклади рівнянь поверхонь, зокрема таких, які ми ще не розглядали.
, бачимо, що його не задовольняють координати жодної точки. Можна навести і інші приклади рівнянь поверхонь, зокрема таких, які ми ще не розглядали. та
та  , означивши їх рівностями
, означивши їх рівностями ,
, ,
,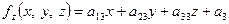 ,
,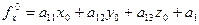 ,
, ,
, .
.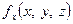 є половиною похідної від функції
є половиною похідної від функції  по змінній
по змінній  , якщо змінні
, якщо змінні  та
та 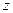 при цьому вважати сталими. Аналогічно,
при цьому вважати сталими. Аналогічно,  та
та  – це половини похідних від функції
– це половини похідних від функції 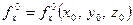 ,
, 
 є значеннями функцій
є значеннями функцій  була серединою хорд, які проходить через неї, згідно з пунктом 2), є виконання рівності
була серединою хорд, які проходить через неї, згідно з пунктом 2), є виконання рівності
 . Тому для відшукання центра поверхні дістаємо систему рівнянь
. Тому для відшукання центра поверхні дістаємо систему рівнянь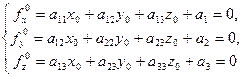 . (4)
. (4) .
. , то система (4) має єдиний розв’язок. У цьому випадку поверхня
, то система (4) має єдиний розв’язок. У цьому випадку поверхня  , то система (4) має безліч, або не має жодного розв’язку. Поверхню
, то система (4) має безліч, або не має жодного розв’язку. Поверхню  .
. . Маємо
. Маємо ,
, . Отже, задана поверхня має єдиний центр, який знаходиться у точці
. Отже, задана поверхня має єдиний центр, який знаходиться у точці  .
.


