
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перетин поверхні з прямою. Частинні випадки.Содержание книги
Поиск на нашем сайте
Перетнемо поверхню другого порядку
та знайдемо точки перетину поверхні
де
1). Нехай 2). Нехай 3). Нехай 4). Випадок 5). При 6). Якщо 7). Якщо
Центр поверхні. Хордою поверхні другого порядку назвемо відрізок, який сполучає дві її довільні точки. Якщо існує точка, в якій усі хорди, що проходять через неї, діляться пополам, то цю точку називають центром поверхні. Центр поверхні є її центром симетрії, оскільки разом із будь-якою точкою поверхні їй належить також точка, симетрична даній відносно центра. Розглянемо питання відшукання центра поверхні, заданої рівнянням (1). Як ми знаємо, умовою того, щоб точка
для довільного напрямку, який задається вектором
Існування та кількість розв’язків системи (4) залежить від її визначника
Якщо Якщо Приклад 1. Знайти центр поверхні, заданої рівнянням
Розв’язання. Складемо та розв’яжемо систему рівнянь
звідки
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.253.84 (0.009 с.) |

 прямою
прямою  , яка проходить через деяку точку
, яка проходить через деяку точку  паралельно до вектора
паралельно до вектора  . Запишемо параметричні рівняння прямої
. Запишемо параметричні рівняння прямої  (2)
(2) , отримуємо квадратне рівняння
, отримуємо квадратне рівняння , (3)
, (3) ,
,


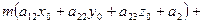

 ,
, 

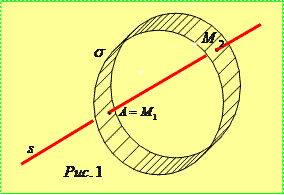 Дослідимо особливості взаємного розташування поверхні
Дослідимо особливості взаємного розташування поверхні  . Одному із коренів рівняння
. Одному із коренів рівняння  , який рівний нулю, відповідає точка
, який рівний нулю, відповідає точка  (рис. 1).
(рис. 1). та рівняння
та рівняння  має два дійсні корені
має два дійсні корені  . Цим кореням відповідають дві точки, які належать заданій поверхні та прямій – це точки
. Цим кореням відповідають дві точки, які належать заданій поверхні та прямій – це точки  . У цьому випадку точка
. У цьому випадку точка  (рис. 2). Якщо дане рівняння має два уявні корені, то пряма буде перетинати поверхню у двох уявних точках, а точка
(рис. 2). Якщо дане рівняння має два уявні корені, то пряма буде перетинати поверхню у двох уявних точках, а точка  . Рівняння
. Рівняння 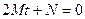 має єдиний корінь
має єдиний корінь  , який визначає першу із точок перетину. Щоб зрозуміти особливість розташування другої точки перетину доцільно дослідити, як змінюється другий корінь рівняння (3) при
, який визначає першу із точок перетину. Щоб зрозуміти особливість розташування другої точки перетину доцільно дослідити, як змінюється другий корінь рівняння (3) при  . У лекції 18, де досліджувались аналогічні питання взаємного розташування лінії другого порядку та прямої, було показано, що при
. У лекції 18, де досліджувались аналогічні питання взаємного розташування лінії другого порядку та прямої, було показано, що при  . Згідно із рівностями (2) при
. Згідно із рівностями (2) при  друга із точок перетину нескінченно віддаляється від точки
друга із точок перетину нескінченно віддаляється від точки  та говорити, що пряма перетинає поверхню у нескінченно віддаленій точці. Напрям прямої
та говорити, що пряма перетинає поверхню у нескінченно віддаленій точці. Напрям прямої  ), або прямої, що проведена паралельно до твірної конуса (рис.
), або прямої, що проведена паралельно до твірної конуса (рис.  ).
). є поєднанням розглянутих вище випадків 1), 2). Рівняння (3) матиме вид
є поєднанням розглянутих вище випадків 1), 2). Рівняння (3) матиме вид  та корені
та корені  . При цьому пряма
. При цьому пряма  точка
точка  , то рівняння (3) не має розв’язків. У цьому випадку пряма
, то рівняння (3) не має розв’язків. У цьому випадку пряма  , то розв’язком рівняння (3) буде довільне дійсне число
, то розв’язком рівняння (3) буде довільне дійсне число 


 була серединою хорд, які проходить через неї, згідно з пунктом 2), є виконання рівності
була серединою хорд, які проходить через неї, згідно з пунктом 2), є виконання рівності
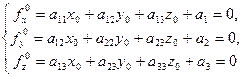 . (4)
. (4) .
. , то система (4) має єдиний розв’язок. У цьому випадку поверхня
, то система (4) має єдиний розв’язок. У цьому випадку поверхня  , то система (4) має безліч, або не має жодного розв’язку. Поверхню
, то система (4) має безліч, або не має жодного розв’язку. Поверхню  .
. . Маємо
. Маємо ,
, . Отже, задана поверхня має єдиний центр, який знаходиться у точці
. Отже, задана поверхня має єдиний центр, який знаходиться у точці  .
.


