
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криві другого порядку: коло, еліпс.Содержание книги
Поиск на нашем сайте
Колом називається множина всіх точок площини, рівновіддалених від даної точки цієї площини, яка називається центром. Рівняння кола з центром у початку координат і радіусом R має вигляд:
Рівняння кола з центом у точці
Рівняння кола у загальному вигляді записують так:
де
Еліпсом називається множина точок площини, сума відстаней яких до двох даних точок, що називаються фокусами, є величина стала, більша за відстань між фокусами. Рівняння еліпса, фокуси якого лежать на осі Ох, має вигляд:
де а – довжина великої півосі; b – довжина малої півосі (ріс 7.1). Залежність між параметрами a,b,c виражається співвідношенням:
Ексцентриситетом еліпса називається відношення фокусної відстані 2с до великої осі 2а:
Якщо центр симетрії еліпса знаходиться у точці
Зразки розв’язування задач. Задача 1. Складіть рівняння кола з центром у точці М(2;-3) і з радіусом, що дорівнює 2. Побудуйте це коло. Розв’язання. За умовою задачі маємо: а=2, b=-3, R=2. Підставивши ці значення в рівняння кола, дістанемо:
або
Будуємо центр кола, тобто точку М(2,-3). З центра М радіусом, який дорівнює 2, опишемо коло (рис.7.2). Задача 2. Складіть рівняння кола, яке має центр в точці (5;-7) і проходить через точку (2;-3). Розв’язання. Знайдемо радіус кола як відстань від центра до його точки:
В рівняння кола підставимо координати центра і знайдену величину радіуса:
Задача 3. Знайдіть координати точок перетину кола Розв’язання. Коло перетинається з віссю абсцис у точках, ординати яких дорівнюють нулю. Припустивши, що рівнянні кола y=0, дістанемо:
Отже, коло перетинається з віссю абсцис у точках (-2; 0) і (8;0). Коло перетинається з віссю ординат у точках, абсциси яких дорівнюють нулю. Припустивши, що в рівнянні кола х=0, дістанемо:
Отже, коло перетинається з віссю ординат у точках
Задача 4. Складіть рівняння кола, яке проходить через точки Розв’язання. Нехай точка
Складемо систему рівнянь відносно невідомих а і b та розв’яжемо її:
Знаходимо Отже, шукане рівняння кола має вигляд:
Задача 5. Знайдіть координати центра і радіус кола Розв’язання. Перепишемо це рівняння у вигляді:
Доповнивши двочлени
Звідки
Задача 6. Скласти рівняння еліпса з фокусами на осі Ох, якщо велика ось дорівнює 12, а відстань між фокусами дорівнює 8.
Розв’язання. З умови впливає, що  і с=4. Знаходимо і с=4. Знаходимо  . Підставивши значення . Підставивши значення 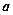 і і  в рівняння еліпса, дістанемо в рівняння еліпса, дістанемо  . .
Задача 7. Дано еліпс Розв’язання. З рівняння еліпса маємо
Задача 8. Скласти рівняння еліпса з фокусами на осі Ох, якщо його велика вісь дорівнює 14, а ексцентриситет Розв’язання. З умови маємо: Далі знаходимо
Задача 9. Скласти рішення еліпса з фокусами на осі Ох, якщо він проходить через точки Розв’язання. Щоб скласти рівняння еліпса, треба знайти параметри
Отже, шукане рівняння має вигляд:
Завдання для самостійної роботи. 1. Складіть рівняння еліпса з фокусами на осі Ох, якщо відстань між фокусами дорівнює 12, ексцентриситет 2. Скласти рівняння еліпса з фокусами на осі Ох, якщо він проходить через точки А (6;4) і В (8;3). 3. Знайдіть відстань між центрами кіл 4. Знайдіть кут між прямими, які проходять через центр кола 5. Складіть рівняння кола, яке проходить через точки А(-8;3) і В(2;-7), якщо центр його лежить на прямий
Криві другого порядку: гіпербола, парабола. I. Гіпербола Гіперболою називається множина точок площини, абсолютна величина різниці відстаней яких до двох даних точок, що називається фокусами, є величина стала (2а), менша за відстань між фокусами (2с). Рівняння гіперболи, фокуси якої лежать на осі на осі Ох, має вигляд:
де а – довжина дійсної півосі;
b – довжина уявної півосі (рис. 8.1). Залежність між параметрами а, b, с виражається співвідношенням:
Ексцентриситетом гіперболи називається відношення півфокусної відстані до її дійсної півосі:
Фокуси гіперболи знаходяться у точках Гіпербола має дві асимптоти, рівняння яких Якщо дійсна та уявна півосі рівні (а=b), то гіпербола називається рівносторонньою. Рівняння рівносторонньої гіперболи має вигляд:
а рівняння її асимптот Якщо фокуси гіперболи лежать на осі Оy у точках
Рівняння асимптот такої гіперболи  , а рівняння директрис , а рівняння директрис  (рис. 8.2). (рис. 8.2).
Гіперболи (8.1) і (8.2) називається спряженими. Рівняння рівносторонньої гіперболи з фокусами на осі Оy має вигляд:
Якщо центр симетрії гіперболи знаходиться у точці
II.Парабола Параболою називають множину точок на площині, рівновіддалених від даної точки, яка називається фокусом і від даної прямої, яка називається директрисою. Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Ох, має вигляд:
де р – параметр параболи.
Якщо  , то вітки параболи напрямлені вправо, якщо , то вітки параболи напрямлені вправо, якщо  , то вітки напрямлені вліво (рис. 8.3). , то вітки напрямлені вліво (рис. 8.3).
Фокус параболи знаходиться у точці Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оy, має вигляд:
Якщо
Якщо вершина параболи – у точці
Фокус цієї параболи
Якщо вершина параболи знаходиться у точці  , а вісь симетрії паралельна осі Ох, то рівняння параболи має вигляд: , а вісь симетрії паралельна осі Ох, то рівняння параболи має вигляд:
Фокус такої параболи
Зразки розв’язування задач. Задача 1. Побудувати гіперболу Розв’язання. Приведемо рівняння кривої до виду (8.1):
Таким чином
Знайдемо відстань фокусів від центра симетрії:
Фокуси гіперболи Ексцентриситет Рівняння асимптот Рівняння директрис
Побудуємо параболу. Задача 2. Скласти рівняння гіперболи з фокусами на осі Ох, якщо її дійсна вісь дорівнює 24, а відстань між фокусами дорівнює Розв’язання. Для складання рівняння гіперболи треба знайти параметри а і b. З умови маємо:
Знайдемо а,с і b:
Підставивши
Задача 3. Скласти рівняння гіперболи за координатами її фокусів Розв’язання. З умови маємо: с=20,
Задача 4. Скласти рівняння гіперболи з фокусами на осі Ох, якщо довжина її дійсної осі дорівнює 16, і гіпербола проходить через точку (-10;-3). Розв’язання. За умовою 2а=16, тобто а=8. Підставивши в рівняння (8.1) значення а=8 і координати даної точки, дістанемо:
Підставивши
Задача 5. Скласти рівняння гіперболи за рівнянням її асимптот Розв’язання. Рівняння асимптот гіперболи
Рівняння гіперболи
Задача 6. Скласти рівняння параболи з вершиною у початку координат, якщо її фокус лежить у точці F (1;0). Розв’язання. Фокус лежить на осі Ох, тобто рівняння параболи має вигляд (8.3)
Задача 7. Скласти рівняння параболи з вершиною у початку координат, яка симетрична відносно осі Оy і проходить через точку А (-2;-4). Розв’язання. Шукана парабола симетрична відносно осі Оy, отже її рівняння має вигляд
Після підстановки значення р в рівняння параболи дістанемо
Задача 8. За даним рівнянням параболи Розв’язання. З рівняння параболи Парабола симетрична відносно осі Ох, її фокус лежить на осі симетрії і має координати
Шукана парабола симетрична відносно осі Ох, її вітки напрямлені вліво. Знайдемо точку, що лежить на параболі. Нехай х=2,  , ,  . .
Задача 9. Побудувати параболу Розв’язання. Знайдемо вершину параболи, перетворивши рівняння
З цього рівняння х0=3,y0=1, С (3;1) – вершина параболи. Знайдемо точки перетину параболи з осями Ох і Оy:
Знайдемо координати фокуса. З рівняння
Рівняння директриси:  , тобто , тобто  ; ;  . .
Задача 10. Побудувати параболу Розв’язання. Знайдемо координати вершини:
Вершина параболи лежить у точці С (0;-2). Вітки параболи напрямлені вправо Знайдемо точку перетину параболи з віссю Ох:
Координати фокуса Рівняння директриси:
Побудуємо параболу. Завдання для самостійної роботи. Задача 1. Скласти рівняння гіперболи з фокусами на осі Ох, якщо довжина її уявної осі дорівнює 12, і гіпербола проходить через точку (20;8). Задача 2. Побудувати гіперболу Задача 3. Скласти рівняння гіперболи, якщо відстань між фокусами дорівнює 10, а рівняння асимптот Задача 4 Скласти рівняння параболи з вершиною у початку координат, яка симетрична відносно осі Ох і проходить через точку (5;-3). Знайти координати фокуса, рівняння директриси. Побудувати. Задача 5 Побудувати параболу
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1916; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.116 (0.009 с.) |

 .
. і радіусом R має вигляд:
і радіусом R має вигляд:
 ,
, - сталі коефіцієнти.
- сталі коефіцієнти. ,
,
 .
. .
. , а осі симетрії паралельні осям
, а осі симетрії паралельні осям  , то рівняння еліпса має вигляд:
, то рівняння еліпса має вигляд: .
.
 .
.
 .
. .
. з осями координат.
з осями координат. ;
; ,
,  .
. ;
; ;
;  .
. і (0;6).
і (0;6). ,
,  ,
,  .
. - центр шуканого кола, тоді
- центр шуканого кола, тоді  , як радіуси того самого кола. Маємо:
, як радіуси того самого кола. Маємо: ,
, ,
, .
.





 .
. .
. .
. .
. .
. і
і  до повних квадратів, дістанемо:
до повних квадратів, дістанемо: або
або  .
. ,
,  ,
,  , тобто центр кола – точка (4;5), а радіус дорівнює 7.
, тобто центр кола – точка (4;5), а радіус дорівнює 7.
 . Знайти координати фокусів еліпса і відстань між ними.
. Знайти координати фокусів еліпса і відстань між ними. і
і  . Тоді
. Тоді 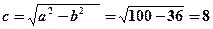 . Отже координати фокусів
. Отже координати фокусів  і
і  , а відстань між ними
, а відстань між ними  .
. .
. ,
,  . Підставивши в це співвідношення значення а, дістанемо
. Підставивши в це співвідношення значення а, дістанемо 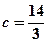 .
.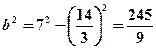 . Отже, шукане рівняння має вигляд:
. Отже, шукане рівняння має вигляд: або
або  .
. і
і  .
. і
і 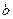 . Підставивши в рівняння еліпса координати даних точок, дістанемо систему рівнянь:
. Підставивши в рівняння еліпса координати даних точок, дістанемо систему рівнянь:

 ;
;  ;
;  ;
; 
 ;
;  ;
;  ;
;  .
. .
. .
. і
і  .
. і через фокуси еліпса
і через фокуси еліпса  .
. , (8.1)
, (8.1)
 .
. .
. ,
,  .
. , а також дві директриси, рівняння яких
, а також дві директриси, рівняння яких  .
. ,
, .
. ,
,  , то її рівняння має вигляд:
, то її рівняння має вигляд: . (8.2)
. (8.2)
 .
. ; (8.1*')
; (8.1*') . (8.2*)
. (8.2*) , (8.3)
, (8.3)
 . Рівняння директриси
. Рівняння директриси  .
. . (8.4)
. (8.4) , рівняння директриси
, рівняння директриси  .
. . (8.4*')
. (8.4*') , рівняння директриси
, рівняння директриси 
 . (8.3*')
. (8.3*') , рівняння директриси
, рівняння директриси  .
. . Знайти фокуси, ексцентриситет, рівняння асимптот та директрис.
. Знайти фокуси, ексцентриситет, рівняння асимптот та директрис. : 144
: 144 ;
; .
. ,
,  ;
; ,
,  - півосі гіперболи.
- півосі гіперболи. .
. ,
, 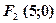 .
. .
. .
. ;
;  .
.
 .
. .
. ,
,  .
. і
і  в рівняння
в рівняння  .
. ,
,  і ексцентриситетом
і ексцентриситетом  .
. . Підставивши у цю рівність с, дістанемо:
. Підставивши у цю рівність с, дістанемо:  , тобто
, тобто  . Далі знайдемо
. Далі знайдемо  . Підставивши
. Підставивши  в рівняння (8.1), дістанемо
в рівняння (8.1), дістанемо  .
. ;
; ;
;  ;
;  .
. .
. і координатами точки, через яку вона проходить
і координатами точки, через яку вона проходить  .
. . За умовою
. За умовою  . Підставимо в рівняння (8.1) координати точки і розв’яжемо систему рівнянь:
. Підставимо в рівняння (8.1) координати точки і розв’яжемо систему рівнянь:

 ;
;  ;
;  ;
;  ;
;  .
. .
. , то
, то  .Підставивши значення р в рівняння (8.3), дістанемо
.Підставивши значення р в рівняння (8.3), дістанемо  .
. ;
; ;
; .
. .
.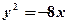 обчислити координати її фокуса, одержати рівняння директриси. Побудувати.
обчислити координати її фокуса, одержати рівняння директриси. Побудувати. ,
, 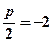 .
. , тобто
, тобто  . Рівняння директриси
. Рівняння директриси  , тобто х=2.
, тобто х=2.
 . Знайти координати фокуса та рівняння директриси.
. Знайти координати фокуса та рівняння директриси. .
. ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
;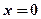 ;
;  ;
;  .
. ,
,  . Координати фокуса
. Координати фокуса  , тобто
, тобто  ,
,  .
.
 . Знайти координати фокуса та рівняння директриси.
. Знайти координати фокуса та рівняння директриси. ;
; .
. .
. ,
,  .
. , тобто
, тобто  ,
,  .
. , тобто
, тобто 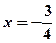 .
.
 . Знайти фокуси, ексцентриситет, рівняння асимптот та директрис.
. Знайти фокуси, ексцентриситет, рівняння асимптот та директрис. .
. . Знайти координати фокуса та рівняння директриси.
. Знайти координати фокуса та рівняння директриси.


