
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поділ відрізка в даному відношенні.Содержание книги
Поиск на нашем сайте
Нехай точки А, В мають координати Якщо відрізок АВ поділимо точкою М у відношенні:
Якщо Зразки розв’язування задач.
Задача 1. Дано ненульові вектори  і і  . Побудувати вектори . Побудувати вектори  , ,  . .
Розв’язання. Знайдемо суму за правилом трикутника
і різницю  : :
Задача 2. Вектори  , ,  - діагоналі паралелограма ABCD. Запишіть вектори - діагоналі паралелограма ABCD. Запишіть вектори  , ,  , ,  і і 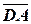 через через  і і  . .
Розв’язання. За означенням суми і різниці векторів маємо: Задача 3. Дано: Розв’язання. Використавши властивості проекцій, дістанемо: 1) 2) Задача 4. Знайти проекції вектора Розв’язання. 1) 2) 3) Задача 5. Знайти периметр трикутника, вершинами якого є точки Розв’язання. Знайдемо координати векторів, що створюють трикутник, та їх довжини:
Тоді периметр трикутника Задача 6. Обчислити довжину вектора Розв’язання. Знайдемо координати векторів:
Тоді довжина шуканого вектора дорівнює:
Задача 7. Відрізок АВ, де Розв’язання.
Отже, Задача 8. Відрізок з кінцями Розв’язання. Знайдемо координати точки М за формулами:
Тоді координати вектора Довжина вектора Задача 9. Точки
Розв’язання. Позначимо координати точки
Четверта вершина паралелограма – точка Задача 10. Знайти напрямні косинуси вектора Розв’язання. Знайдемо координати вектора Напрямні косинуси дорівнюють:
Тоді Завдання для самостійної роботи. Задача 1. У трикутнику АВС проведено медіану АМ. Доведіть, що Задача 2. Дано вектори Задача 3. Точки
Задача 4. Дано: Задача 5. Відрізок АВ задано координатами своїх кінців 4. Скалярний, векторний, мішаний добутки векторів. Застосування в задачах геометрії. Умови перпендикулярності та компланарності векторів. 1. Скалярним добутком векторів називається число, що дорівнює добутку довжин векторів на косинус кута між ними:
Якщо вектори задані своїми координатами:
Кут між векторами обчислюють за формулою:
Умова перпендикулярності векторів
Скалярний квадрат вектора дорівнює:
Проекція вектора
2. Векторним добутком двох векторів 1) 2) 3)
 утворюють праву трійку векторів, тобто третій вектор має такий напрям, що при спостереженні з його кінця найближчий поворот від вектора утворюють праву трійку векторів, тобто третій вектор має такий напрям, що при спостереженні з його кінця найближчий поворот від вектора  до до  виконується проти годинникової стрілки. виконується проти годинникової стрілки.
Векторний добуток позначається символом Модуль векторного добутку дорівнює площі паралелограма, побудованого на
Площа трикутника обчислюється за формулою:
Векторній добуток векторів, які задані своїми координатами, обчислюються за формулою:
Умова колінеарності двох векторів
Векторні добутки ортів дорівнюють:
3. Мішаним добутком трьох векторів називається добуток Частіше мішаний добуток позначається Якщо вектори задані своїми координатами, то мішаний добуток знаходять за формулою:
Об’єм паралелепіпеду, який побудований на векторах
Для об’єму піраміди маємо наступну формулу:
Умова компланарності трьох векторів має вигляд: Зразки розв’язування задач. Задача 1. Знайти скалярний добуток векторів Розв’язання. Знайдемо координати векторів: Задача 2. Знайти кут між діагоналями паралелограма, який побудований на векторах Розв’язання. Як відомо, діагоналі паралелограма є
Тоді косинус кута між діагоналями знаходиться за формулою:
Задача 3. Задано вектори Розв’язання. Знайдемо координати векторів Обчислимо проекцію
Задача 4. Дано трикутник своїми вершинами: Розв’язання. Знайдемо координати векторів:
Умова перпендикулярності двох векторів має вигляд: Доведено, що вектори перпендикулярні. Задача 5. Знайти площу паралелограма, який побудований на векторах Розв’язання. Модуль векторного добутку двох векторів дорівнює площі паралелограма, який побудований на цих векторах. Знайдемо векторний добуток:
Площа паралелограма дорівнює:
Задача 6. Знайти площу трикутника за координатами його вершин: Розв’язання. Розглянемо два вектори, на яких побудовано трикутник, наприклад,
Векторний добуток дорівнює:
Тоді площа трикутника дорівнює:
Задача 7. Розкрити дужки та спростити вираз:
Розв’язання.
Задача 8. При яких значеннях α і β вектори Розв’язання. Умова колінеарності двох векторів має вигляд:
Звідки
Задача 9. Обчислити об’єм паралелепіпеду і піраміди, які побудовані на векторах Розв’язання. Об’єм паралелепіпеду дорівнює модулю мішаного добутку векторів
Тоді об’єми паралелепіпеду і піраміди дорівнюють:
Задача 10. Довести, що точки Розв’язання. Щоб довести, що ці чотири точки лежать в одній площині, доведемо, що в одній площині лежать вектори Умова компланарності трьох векторів має вигляд:
Знайдемо координати векторів:
Обчислимо мішаний добуток векторів:
Таким чином, точки A, B, C, D лежать в одній площині. Завдання для самостійної роботи. Задача 1. Знайти кут між векторами Задача 2. Обчислити проекцію вектора Задача 3. Дано вектори: Довести: 1) вектори 2) вектори 3) вектори Задача 4. Обчислити об’єм паралелепіпеда, побудованого на векторах: Задача 5. Дано координати вершин піраміди:: 1) кут АВС; 2) площу грані АВС; 3) об’єм піраміди ОАВС.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 832; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.238.244 (0.01 с.) |

 ,
,  .
. , то координати точки М знаходять за формулами:
, то координати точки М знаходять за формулами: ;
; 
 .
. , то отримуємо формули для знаходження координат середини відрізка.
, то отримуємо формули для знаходження координат середини відрізка.


 ,
,  . Додавши ці рівності, дістанемо
. Додавши ці рівності, дістанемо  . Далі знайдемо
. Далі знайдемо  ;
;  ,
,  .
. ;
;  . Обчислити: 1)
. Обчислити: 1)  ; 2)
; 2)  .
. .
. .
. ;
; ;
; .
. ,
,  ,
,  .
. ,
,  ;
; ,
,  ;
; ,
,  ;
; ;
; ;
; .
. .
. , якщо
, якщо  ,
,  .
. ,
,  ;
; ,
, 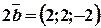 ;
; ,
,  .
. .
. ,.
,.  , поділений точкою М у відношенні
, поділений точкою М у відношенні  . Знайти координати точки М.
. Знайти координати точки М. ;
;  ;
; .
. .
. і
і  , ділиться в точці М навпіл. Знайдіть довжину відрізка МК, де
, ділиться в точці М навпіл. Знайдіть довжину відрізка МК, де  .
. ;
; 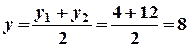 ;
;  ;
; .
. ,
,  .
. .
. ,
,  ,
,  є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D.
є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D.
 , тоді
, тоді  ,
,  . Оскільки
. Оскільки  , їх координати рівні:
, їх координати рівні: ;
;  ;
;  ;
; ;
;  ;
;  .
. .
. та його довжину
та його довжину  .
. ;
;  ;
;  .
. ;
;  ;
;  .
. .
. ,
,  ,
,  . Знайти довжини векторів 1)
. Знайти довжини векторів 1)  , 2)
, 2)  .
. ,
,  ,
,  є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D, а також периметр паралелограму.
є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D, а також периметр паралелограму. ,
,  , кути між віссю l дорівнюють 600 і 1200. Обчислити
, кути між віссю l дорівнюють 600 і 1200. Обчислити  .
.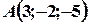 і
і  . Знайти довжину вектора
. Знайти довжину вектора  .
.
 ,
,  , то скалярний добуток обчислюють за формулою:
, то скалярний добуток обчислюють за формулою: .
. .
. .
. .
. .
. , який задовольняє умові:
, який задовольняє умові: ;
; ,
,  ;
;
 . За визначенням випливає, що
. За визначенням випливає, що  .
. .
. .
. .
. (або
(або  ).
).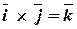 ;
;  ;
;  ;
; ;
;  ;
;  .
. .
. .
. .
. ,
,  ,
,  як на сторонах, дорівнює модулю мішаного добутку цих векторів:
як на сторонах, дорівнює модулю мішаного добутку цих векторів: .
.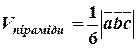 .
. .
. ,
,  .
.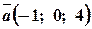 ,
,  . Тоді скалярний добуток дорівнює
. Тоді скалярний добуток дорівнює  .
. ,
,  .
. та
та  . Знайдемо ці вектори:
. Знайдемо ці вектори: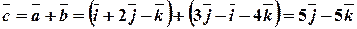 ;
; ;
; ;
; .
.
 .
. ,
,  ,
,  . Обчислити проекцію вектора
. Обчислити проекцію вектора  на вектор
на вектор  ;
;  та
та  .
. на вектор
на вектор  .
. ,
,  ,
,  . Покажіть, що
. Покажіть, що  .
. ;
;  ;
; ;
;  .
. . Перевіримо виконання цієї умови:
. Перевіримо виконання цієї умови:  .
. ,
, 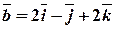 .
.
 .
. ,
,  ,
,  .
. .
. ,
,  .
.
 .
.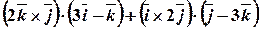 .
.
 ,
,  колінеарні?
колінеарні? .
. ;
;  .
. ,
,  ,
,  .
.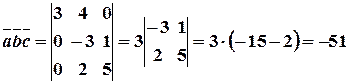 .
. ;
; .
. ,
,  ,
,  ,
,  лежать в одній площині.
лежать в одній площині. ,
,  , тобто ці три вектори компланарні.
, тобто ці три вектори компланарні. .
. ;
;  ;
;  .
. .
. і
і  , а також площу паралелограма, побудованого на них.
, а також площу паралелограма, побудованого на них. на вектор
на вектор  ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  ,
,  . Обчислити:
. Обчислити:


