
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричний метод роз’язання лінійних систем.Содержание книги
Поиск на нашем сайте
Нехай дано систему: Розглянемо три матриці:
Перша матриця називається матрицею симтеми, друга матрицею-стовпцем змінних, третя – матрицею-стовпцем вільних членів. Тоді систему можна записати у матричному вигляді:
Зразки розв’язування задач. 1. Розв’язати системи рівнянь за формулами Крамера:
Розв’язання: a) Заходимо визначник системи
За формулами Крамера, маємо:
б) Знаходимо визначник системи:
Система має єдиний розв’язок. Знаходимо
За формулами Крамера, маємо:
2. Дослідити на сумісність системи лінійних рівнянь та знайти їх розв’язок у випадку сумісності: а) Розв’язання: a) Обчислемо визначник системи:
Визначник системи дорівнює нулю. Система або має безліч розв’язків, або не має жодного розв’язку. Знаходимо
Оскільки,
Розв’язуємо отриману систему за формулами Крамера:
б) Система або має безліч розв’язків, або не має жодного розв’язку.
Отже, задана система не має жодного розв’язку, тобто вона є несумісною. 3. Розв’язати систему лінійних рівнянь матричним методом:
Розв’язання: Запишемо дану систему рівнянь у матричній формі:
Знайдемо алгебричні доповнення елементів матриці А:
Скориставшись рівністю
Завдання для самостійної роботи. 1. Розв’язати системи лінійних рівнянь за формулами Крамера: а) 2. Визначити, при яких значеннях а і b система
а) має один розв’язок; б) має безліч розв’язків; в) не має жодного розв’язку. 3. Розв’язати системи лінійних рівнянь матричним методом: а)
3.Вектори в просторі. Основні поняття. Лінійні операції з векторами. Прямокутна система координат у просторі. Розглянемо напрямлений відрізок Довжину вектора будемо позначати таким чином:
Додавання векторів.
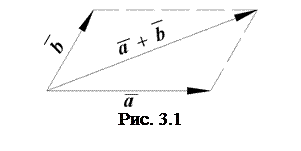
Щоб побудувати суму даних векторів  і і  , треба відкласти ці вектори від довільної точки та побудувати на них паралелограм. Сумою векторів буде діагональ, що виходить з початку векторів , треба відкласти ці вектори від довільної точки та побудувати на них паралелограм. Сумою векторів буде діагональ, що виходить з початку векторів  і і  (рис. 3.1). (рис. 3.1).
Цей спосіб побудови називається правилом паралелограма. Суму двох векторів можно побудувати ще й за правилом трикутника.
Відкласти вектор  від кінця вектора від кінця вектора  . Сумою векторів . Сумою векторів  і і  буде вектор, що з’єднує початок буде вектор, що з’єднує початок  з кінцем з кінцем  (рис. 3.2). (рис. 3.2).
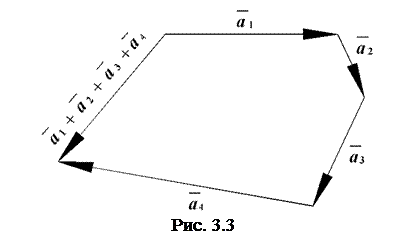
Щоб побудувати суму n даних векторів  , треба від довільної точки відкласти , треба від довільної точки відкласти  , потім від його кінця відкласти , потім від його кінця відкласти  і т.д., нарешті від кінця і т.д., нарешті від кінця  відкласти відкласти  . Сумою векторів буде вектор, напрямлений від початку . Сумою векторів буде вектор, напрямлений від початку  до кінця до кінця  (рис. 3.3). (рис. 3.3).
Віднімання векоторів.
Щоб побудувати різницю векторів  , треба відкласти ці вектори від довільної точки, з’єднати їх кінці та вибрати на цьому відрізку напрямок від кінця , треба відкласти ці вектори від довільної точки, з’єднати їх кінці та вибрати на цьому відрізку напрямок від кінця  до кінця до кінця  (рис. 3.4). (рис. 3.4).
Множення вектора на число. Добутком ненульового вектора Ці три операції називаються лінійними операціями з векторами. Проекція вектора на вісь.
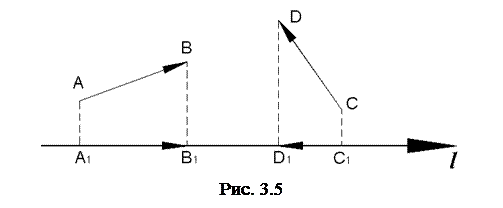
Проекцією вектора на вісь називається довжина направленого відрізка, початок якого є проекція початку вектора і кінець – проекція його кінця, яка береться із знаком плюс, якщо напрями відрізка і осі збігаються, і зі знаком мінус, якщо їх напрями протилежні (рис.3.5).
Властивості проекції. a) б) в) Прямокутна система координат. Нехай у просторі задано три попарно перпендикулярні осі OX, OY, OZ. Координатами вектора
Якщо Якщо Правила дій над векторами, заданими своїми координатами. Якщо
Довжина вектора. Напрямлені косинуси вектора.
де Для напрямлених конусів справедливо співвідношення:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.32.238 (0.006 с.) |


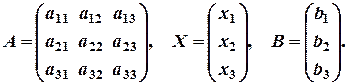
 . Якщо матриця системи рівнянь невироджена
. Якщо матриця системи рівнянь невироджена  , то розв’язок системи знаходимо у вигляді
, то розв’язок системи знаходимо у вигляді  , або
, або


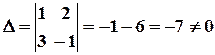 , тому система має єдиний розв’язок. Знаходимо
, тому система має єдиний розв’язок. Знаходимо 
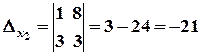 .
.




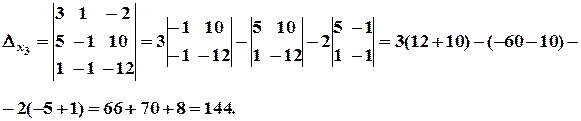

 б)
б) 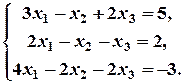




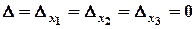 , то система сумісна і невизначена. Для знаходження всіх розв’язків, відкидаємо третє рівняння, а рівняння, що залишилися, записуємо у вигляді:
, то система сумісна і невизначена. Для знаходження всіх розв’язків, відкидаємо третє рівняння, а рівняння, що залишилися, записуємо у вигляді: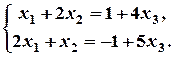


 ;
;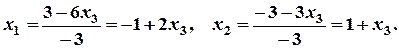
 , тому що другий і третій рядки пропорційні.
, тому що другий і третій рядки пропорційні.

 де
де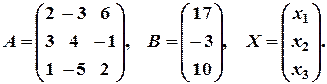
 значить матриця А має обернену матрицю.
значить матриця А має обернену матрицю.
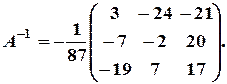
 , знаходимо розв’язок системи:
, знаходимо розв’язок системи:
 - шуканий розв’язок.
- шуканий розв’язок. б)
б) 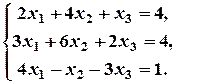

 б)
б) 
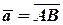 , де А – початок, В – кінець. Будемо називати його вектором.
, де А – початок, В – кінець. Будемо називати його вектором. .
.


 , і протинапрям, якщо
, і протинапрям, якщо  (при
(при  ,
,  ).
).
 ,
, 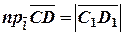 .
. ;
; ;
; .
.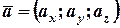 на осі називаються проекції вектора на ці осі:
на осі називаються проекції вектора на ці осі: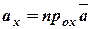 ,
, 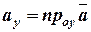 ,
,  .
. - одиничні вектори, що напрямлені по OX, OY, OZ, то
- одиничні вектори, що напрямлені по OX, OY, OZ, то 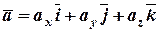 .
. ,
,  то координати вектора
то координати вектора 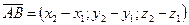 .
.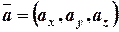 ,
, 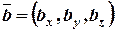 , то
, то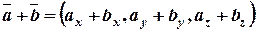 ;
; ;
;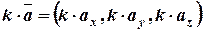 .
. ;
; ;
; 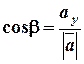 ;
;  ,
,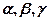 - кути між
- кути між 



