
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Міністерство освіти І науки україниСодержание книги
Поиск на нашем сайте
Міністерство освіти І науки україни Національна металургійна академія україни Т.М.КАДИЛЬНИКОВА, О.Є.ЗАПОРОЖЧЕНКО, Т.П.БАС ПОСІБНИК-ДОВІДНИК з дисципліни “Вища математика” для студентів заочної форми навчання (І семестр, I курс) Затверджено На засіданні Вченої Ради Академії Протокол № від 2010 р. Дніпропетровськ НМетАУ 2010
УДК 517(07) Кадильникова Т.М., Запорожченко О.Є., Бас Т.П.Вища математика в прикладах та задачах. Частина I: Навч. посібник.- Дніпропетровськ: НМетАУ, 2010.- 92 с. Наведені докладні розв’язання типових задач з додатковии поясненнями теоретичних положень. Посібник призначений для студентів всіх форм навчання. Друкується за авторською редакцією.
Відповідальний за випуск А.П.Павленко, д-р. фіз.-мат. наук, професор. Рецензенти: Т.С.Кагадій, докт. фіз.-мат. наук, проф. (НГУ); Ю.Я.Годес, канд. фіз.-мат. наук, доц. (ДНУ).
Національна металургійна академія України, 2010 Вступ Розв’язання задач з вищої математики часто пов’язано з багатьма складностями. Відомо, що при самостійному розв’язуванні задач студентам потрібні постійні консультації щодо способів їх розв’язування, оскільки знайти шлях до розв’язування задачі без допомоги викладача або відповідного підручника студентові не під силу. Допомогти студентам заочної форми навчання подолати ці складності, навчити їх застосовувати теоретичні знання до розв’язування задач - основне призначення цього методичного видання. Метою видання є надання допомоги студентам у отриманні навичок з розв’язування типових задач, користуючись наведеними теоремами та формулами, а також детально розібраними прикладами. Там, де це можливо, задачі класифікувалися за темами. До кожного нового типу подано задачі з розв’язуванням і кілька задач того самого типу для самостійного опрацювання. 1. Матриці і операції над ними. Визначники матриць. Властивості визначників. Обернена матриця. Матрицею розміру
Перший індекс кожного елемента вказує на номер рядка, в якому цей елемент розміщений, другий – на номер стовпця. Матриці позначають прописними буквами латинського алфавіту: А, В, C,…. Уживають також більш компактний запис А=(а ij)mn.
Матриця називається числовою, якщо її елементи аij – числа; функціональною, якщо аij – функції. Ми будемо розглядати, в основному, числові матриці. Кажуть, що матриці А і В мають однакові розміри, якщо у них однакова кількість рядків і однакова кількість стовпців. Матриці А і В вважаються рівними між собою, якщо вони мають однакові розміри, а їхні елементи, що знаходяться на однакових місцях, рівні між собою. Матриця, у якої кількість рядків дорівнює кількості стовпців (тобто m = n), називається квадратною матрицею порядку n. Квадратна матриця порядку n має вигляд:
Елементи а11, a22,…,ann утворюють головну діагональ матриці, а елементи a1n, a2(n-1),…,an1 – побічну. Деякі квадратні матриці мають власні назви. Зокрема, до них відносяться нульова, діагональна та одинична матриці. Нульовою називається матриця, всі елементи якої - нулі. Якщо всі елементи матриці, окрім розташованих на головній діагоналі, дорівнюють нулю, то в цьому випадку матриця називається діагональною. Якщо всі елементи діагональної матриці дорівнюють одиниці, то вона називається одиничною матрицею. Одинична матриця має вигляд:
Матрицю, яку одержують із матриці А заміною її рядків відповідними стовпцями, називають транспонованою і позначають АТ. Транспонована матриця має вигляд:
Сумою (різницею) матриць А і В називається матриця С, елементи якої сij=aij+bij (сij=aij-bi j), де aij і bij – відповідно елементи матриць А і В. При цьому пишуть С = А + В. Додавати або віднімати можна тільки матриці однакових розмірів. Добутком матриці А на число α називається матриця С такого ж розміру, елементи якої сij=α aij, де ai j – елементи матриці А, тобто при множенні матриці на число (числа на матрицю) треба всі елементи матриці помножити на це число. При цьому пишуть С = α А. Для довільних матриць А, В, С однакових розмірів і довільних чисел α та β справджуються рівності: А + В = В + А; (А + В) +С = А + (В + С); α (А + В) = α А + α В; ( α + β )А = α А + β А; ( α β )А = α ( β А). Добутком матриці
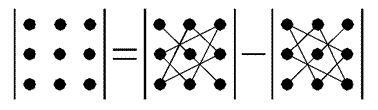
Якщо АВ = ВА, то матриці А і В називаються комутативними. Визначником другого порядку квадратної матриці Визначником третього порядку квадратної матриці
Для обчислення визначників третього порядку існує правило трикутника, яке схематично можна зобразити так: Аналогічно для квадратної матриці А n-го порядку можна розглянути її визначник n-го порядку. Визначник матриці А часто позначають det A. Мінором Мij елемента аij називається визначник, який дістають з визначника матриці А викреслюванням i -го рядка та j -го стовпця. Алгебричним доповненням Аij елемента аij називається відповідний мінор, взятий зі знаком «плюс», якщо сума його індексів парна, і зі знаком «мінус», якщо сума його індексів непарна Визначник вищого порядку можна обчислити за допомогою визначників нижчого порядку розкладом за елементами якогось рядка або стовпця. Зокрема, для визначників третього порядку маємо:
Визначник дорівнює сумі добутків елементів деякого рядка (стовпця) на їх алгебричні доповнення. Зразки розв’язування задач. 1. Знайти матрицю Розв’язання: Користуючись означеннями операцій множення матриці на число та додавання матриць, послідовно знаходимо:
2. Для матриць Р озв’язання:
3. Для заданих матриць обчислити АВ і ВА, якщо це можливо: a) Розв’язання: а) Оскільки задано матриці А2×2 і В2×2, то можна визначити добутки АВ та ВА. Отже,
АВ=ВА. б) Оскільки кількість стовпців матриці А не дорівнює кількості рядків матриці В то добутку АВ не існує. Проте можна обчислити добуток ВА.
4. Обчислити визначники: а) Розв’язання:
а) Використовуючи формулу для обчислення визначника другого порядку, маємо: б) в) Користуючись правилом трикутника, знаходимо
5. Обчислити визначник Розв’язання:
6. Обчислити визначник, спочатку спростивши його: Розв’язання: Додамо перший рядок до третього рядка, потім помножимо перший рядок на –2 і додамо його до другого рядка і отримаємо визначник, в якому елементи
7. Знайти матрицю, обернену до матриці Розв’язання: Знайдемо визначник матриці:
Перевіримо, чи виконуються рівності
Отже Завдання для самостійної роботи. 1. Для матриць 2. Обчислити визначники: а) 3. Обчислити визначник матриці, яка є добутком двох заданих матриць:
4. Серед заданих матриць знайти невироджену: а) 5. Для заданої матриці знайти обернену: 2. Системи лінійних рівнянь. Формули Крамера. Розв’язування систем лінійних рівнянь матричним методом Системою m лінійних рівнянь з n змінними x1, x2, …, xn називається система, яка має наступний вигляд: де аij – коефіцієнти при змінних; bi -вільні члени, Упорядкована сукупність чисел
Система, що має розв’язок, називається сумісною. Система, яка не має жодного розв’язку, називається несумісною. Система з єдиним розв’язком називається визначеною, а з більшим числом розв’язків – невизначаною. Система двох лінійних рівнянь з двома змінними має вигляд:
а систему трьох лінійних рівнянь з трьома змінними записують у вигляді: Метод Крамера. Цей метод розв’язування систем лінійних рівнянь зводиться до обчислення визначників. Так, розв’язок системи (2.1) можна знайти за формулами Крамера:
де
Формули Крамера для системи (2.2) мають вигляд:
де
Системи (2.1) і (2.2) мають: а) єдиний розв’язок, коли б) безліч розв’язків, коли в) не мати жодного розв’язку, коли Зразки розв’язування задач. 1. Розв’язати системи рівнянь за формулами Крамера:
Розв’язання: a) Заходимо визначник системи
За формулами Крамера, маємо:
б) Знаходимо визначник системи:
Система має єдиний розв’язок. Знаходимо
За формулами Крамера, маємо:
2. Дослідити на сумісність системи лінійних рівнянь та знайти їх розв’язок у випадку сумісності: а) Розв’язання: a) Обчислемо визначник системи:
Визначник системи дорівнює нулю. Система або має безліч розв’язків, або не має жодного розв’язку. Знаходимо
Оскільки,
Розв’язуємо отриману систему за формулами Крамера:
б) Система або має безліч розв’язків, або не має жодного розв’язку.
Отже, задана система не має жодного розв’язку, тобто вона є несумісною. 3. Розв’язати систему лінійних рівнянь матричним методом:
Розв’язання: Запишемо дану систему рівнянь у матричній формі:
Знайдемо алгебричні доповнення елементів матриці А:
Скориставшись рівністю
Завдання для самостійної роботи. 1. Розв’язати системи лінійних рівнянь за формулами Крамера: а) 2. Визначити, при яких значеннях а і b система
а) має один розв’язок; б) має безліч розв’язків; в) не має жодного розв’язку. 3. Розв’язати системи лінійних рівнянь матричним методом: а)
3.Вектори в просторі. Основні поняття. Лінійні операції з векторами. Прямокутна система координат у просторі. Розглянемо напрямлений відрізок Довжину вектора будемо позначати таким чином:
Додавання векторів.
Щоб побудувати суму даних векторів  і і  , треба відкласти ці вектори від довільної точки та побудувати на них паралелограм. Сумою векторів буде діагональ, що виходить з початку векторів , треба відкласти ці вектори від довільної точки та побудувати на них паралелограм. Сумою векторів буде діагональ, що виходить з початку векторів  і і  (рис. 3.1). (рис. 3.1).
Цей спосіб побудови називається правилом паралелограма. Суму двох векторів можно побудувати ще й за правилом трикутника.
Відкласти вектор  від кінця вектора від кінця вектора  . Сумою векторів . Сумою векторів  і і  буде вектор, що з’єднує початок буде вектор, що з’єднує початок  з кінцем з кінцем  (рис. 3.2). (рис. 3.2).
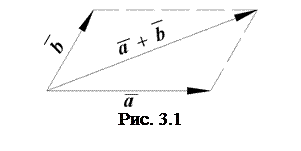
Щоб побудувати суму n даних векторів  , треба від довільної точки відкласти , треба від довільної точки відкласти  , потім від його кінця відкласти , потім від його кінця відкласти  і т.д., нарешті від кінця і т.д., нарешті від кінця  відкласти відкласти  . Сумою векторів буде вектор, напрямлений від початку . Сумою векторів буде вектор, напрямлений від початку  до кінця до кінця  (рис. 3.3). (рис. 3.3).
Віднімання векоторів.
Щоб побудувати різницю векторів  , треба відкласти ці вектори від довільної точки, з’єднати їх кінці та вибрати на цьому відрізку напрямок від кінця , треба відкласти ці вектори від довільної точки, з’єднати їх кінці та вибрати на цьому відрізку напрямок від кінця  до кінця до кінця  (рис. 3.4). (рис. 3.4).
Множення вектора на число. Добутком ненульового вектора Ці три операції називаються лінійними операціями з векторами. Проекція вектора на вісь.
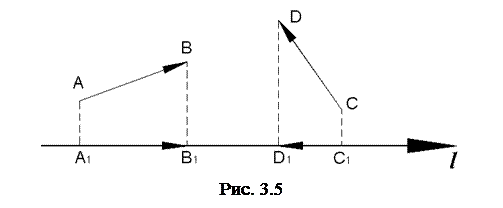
Проекцією вектора на вісь називається довжина направленого відрізка, початок якого є проекція початку вектора і кінець – проекція його кінця, яка береться із знаком плюс, якщо напрями відрізка і осі збігаються, і зі знаком мінус, якщо їх напрями протилежні (рис.3.5).
Властивості проекції. a) б) в) Зразки розв’язування задач.
Задача 1. Дано ненульові вектори  і і  . Побудувати вектори . Побудувати вектори  , ,  . .
Розв’язання. Знайдемо суму за правилом трикутника
і різницю  : :
Задача 2. Вектори  , ,  - діагоналі паралелограма ABCD. Запишіть вектори - діагоналі паралелограма ABCD. Запишіть вектори  , ,  , ,  і і 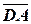 через через  і і  . .
Розв’язання. За означенням суми і різниці векторів маємо: Задача 3. Дано: Розв’язання. Використавши властивості проекцій, дістанемо: 1) 2) Задача 4. Знайти проекції вектора Розв’язання. 1) 2) 3) Задача 5. Знайти периметр трикутника, вершинами якого є точки Розв’язання. Знайдемо координати векторів, що створюють трикутник, та їх довжини:
Тоді периметр трикутника Задача 6. Обчислити довжину вектора Розв’язання. Знайдемо координати векторів:
Тоді довжина шуканого вектора дорівнює:
Задача 7. Відрізок АВ, де Розв’язання.
Отже, Задача 8. Відрізок з кінцями Розв’язання. Знайдемо координати точки М за формулами:
Тоді координати вектора Довжина вектора Задача 9. Точки
Розв’язання. Позначимо координати точки
Четверта вершина паралелограма – точка Задача 10. Знайти напрямні косинуси вектора Розв’язання. Знайдемо координати вектора Напрямні косинуси дорівнюють:
Тоді Завдання для самостійної роботи. Задача 1. У трикутнику АВС проведено медіану АМ. Доведіть, що Задача 2. Дано вектори Задача 3. Точки Задача 4. Дано: Задача 5. Відрізок АВ задано координатами своїх кінців 4. Скалярний, векторний, мішаний добутки векторів. Застосування в задачах геометрії. Умови перпендикулярності та компланарності векторів. 1. Скалярним добутком векторів називається число, що дорівнює добутку довжин векторів на косинус кута між ними:
Якщо вектори задані своїми координатами:
Кут між векторами обчислюють за формулою:
Умова перпендикулярності векторів
Скалярний квадрат вектора дорівнює:
Проекція вектора
2. Векторним добутком двох векторів 1) 2) 3)
 утворюють праву трійку векторів, тобто третій вектор має такий напрям, що при спостереженні з його кінця найближчий поворот від вектора утворюють праву трійку векторів, тобто третій вектор має такий напрям, що при спостереженні з його кінця найближчий поворот від вектора  до до  виконується проти годинникової стрілки. виконується проти годинникової стрілки.
Векторний добуток позначається символом Модуль векторного добутку дорівнює площі паралелограма, побудованого на
Площа трикутника обчислюється за формулою:
Векторній добуток векторів, які задані своїми координатами, обчислюються за формулою:
Умова колінеарності двох векторів
Векторні добутки ортів дорівнюють:
3. Мішаним добутком трьох векторів називається добуток Частіше мішаний добуток позначається | |||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

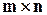
 називається сукупність елементів
називається сукупність елементів  ai j, розміщених у вигляді прямокутної таблиці, що має m рядків і n стовпців:
ai j, розміщених у вигляді прямокутної таблиці, що має m рядків і n стовпців: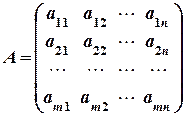 або
або 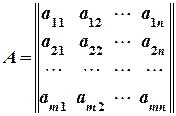 .
.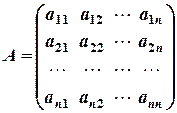 .
. .
.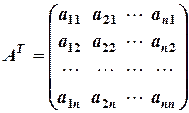 .
.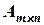 на матрицю
на матрицю  називається матриця
називається матриця  , елементи якої
, елементи якої 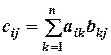 , де aik, bkj – елементи матриць А і В. Зауважимо, що перемножувати можна тільки ті матриці, в яких кількість стовпців першої матриці дорівнює кількості рядків другої. З існування добутку АВ не означає, що існує добуток ВА.
, де aik, bkj – елементи матриць А і В. Зауважимо, що перемножувати можна тільки ті матриці, в яких кількість стовпців першої матриці дорівнює кількості рядків другої. З існування добутку АВ не означає, що існує добуток ВА.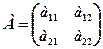 називається число
називається число 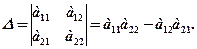
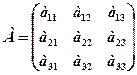 називається число:
називається число: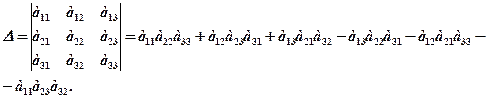
 .
.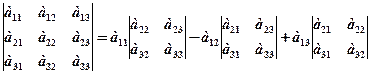 .
.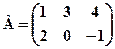 і
і 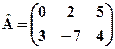 .
.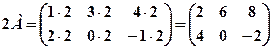 ,
,  ,
,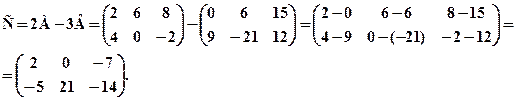
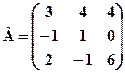 і
і 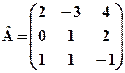 обчислити АТ+ВТ.
обчислити АТ+ВТ.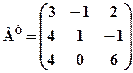 ,
,  ,
, .
. ,
, 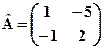 ; б)
; б) 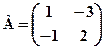 ,
, 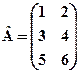 .
.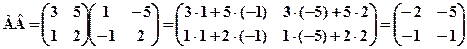 ;
;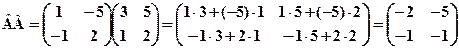 ;
; .
.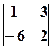
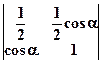 ; в)
; в) 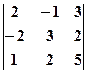 .
.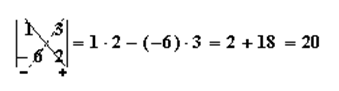
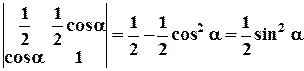 .
.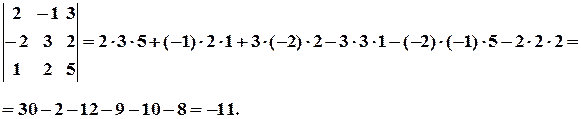
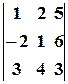 , розклавши його за елементами першого рядка.
, розклавши його за елементами першого рядка.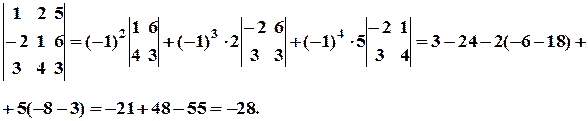
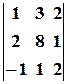 .
.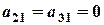 . Отриманий визначник розкладаємо за елементами першого стовпця:
. Отриманий визначник розкладаємо за елементами першого стовпця:
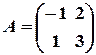 і перевірити, чи справджуються рівності
і перевірити, чи справджуються рівності 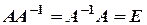 .
. .Оскільки
.Оскільки 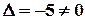 , обернена матриця
, обернена матриця  існує. Знаходимо алгебричні доповнення: А11= 3, А12= -1, А21 = -2, А22 = 1. Тоді обернена матриця буде мати вигляд:
існує. Знаходимо алгебричні доповнення: А11= 3, А12= -1, А21 = -2, А22 = 1. Тоді обернена матриця буде мати вигляд:  .
.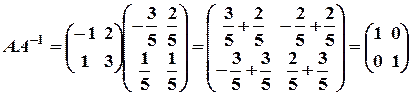 ;
;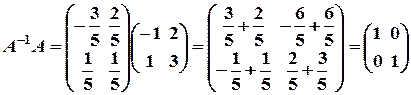 .
. і
і  обчислити АТ-3В, АВ, ВА, АВ+Е.
обчислити АТ-3В, АВ, ВА, АВ+Е.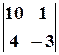 , б)
, б) 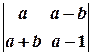 , в)
, в)  , г)
, г) 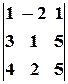 .
.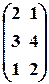 ,
, 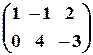 .
.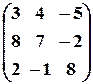 , б)
, б) 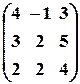 , в)
, в) 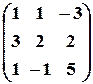 .
.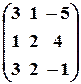 .
.
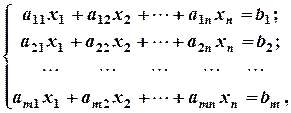
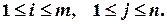
 , називається розв’язком системи, якщо при заміні х1 на а1, х2 на а2, …, хn на аn у кожному рівнянні системи дістанемо n правильних числових рівностей.
, називається розв’язком системи, якщо при заміні х1 на а1, х2 на а2, …, хn на аn у кожному рівнянні системи дістанемо n правильних числових рівностей.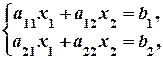 (2.1)
(2.1)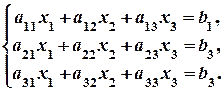 (2.2)
(2.2)
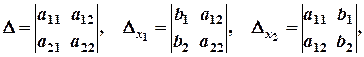 за умови, що
за умови, що 
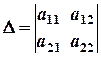 - називається визначником системи (2.1), а
- називається визначником системи (2.1), а  - визначники, які дістають з визначника
- визначники, які дістають з визначника 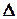 заміною першого, другого стовпців відповідно стовпцем вільних членів.
заміною першого, другого стовпців відповідно стовпцем вільних членів.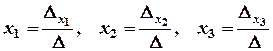 ,
,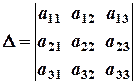
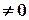 - визначник системи (2.2), а
- визначник системи (2.2), а визначники, які дістають з визначника
визначники, які дістають з визначника  ;
;
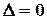 і хоча б один із визначників
і хоча б один із визначників 
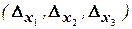 відмінний від нуля.
відмінний від нуля.

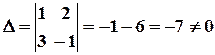 , тому система має єдиний розв’язок. Знаходимо
, тому система має єдиний розв’язок. Знаходимо 
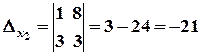 .
.




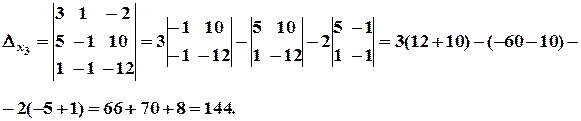

 б)
б) 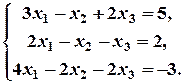




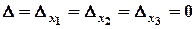 , то система сумісна і невизначена. Для знаходження всіх розв’язків, відкидаємо третє рівняння, а рівняння, що залишилися, записуємо у вигляді:
, то система сумісна і невизначена. Для знаходження всіх розв’язків, відкидаємо третє рівняння, а рівняння, що залишилися, записуємо у вигляді: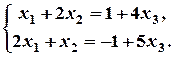


 ;
;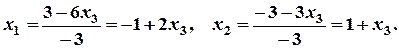
 , тому що другий і третій рядки пропорційні.
, тому що другий і третій рядки пропорційні.

 де
де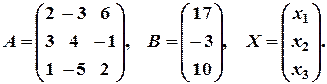
 значить матриця А має обернену матрицю.
значить матриця А має обернену матрицю.
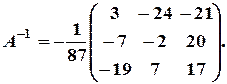
 , знаходимо розв’язок системи:
, знаходимо розв’язок системи:
 - шуканий розв’язок.
- шуканий розв’язок. б)
б) 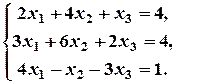

 б)
б) 
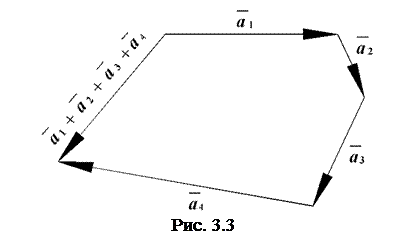
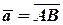 , де А – початок, В – кінець. Будемо називати його вектором.
, де А – початок, В – кінець. Будемо називати його вектором. .
.


 , і протинапрям, якщо
, і протинапрям, якщо  (при
(при  ,
,  ).
).
 ,
, 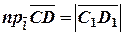 .
. ;
; ;
; .
.


 ,
,  . Додавши ці рівності, дістанемо
. Додавши ці рівності, дістанемо  . Далі знайдемо
. Далі знайдемо  ;
;  ,
,  .
. ;
;  . Обчислити: 1)
. Обчислити: 1)  ; 2)
; 2)  .
. .
. .
. ;
; ;
; .
. ,
,  ,
,  .
. ,
,  ;
; ,
,  ;
; ,
,  ;
; ;
; ;
; .
. .
. , якщо
, якщо  ,
,  .
. ,
,  ;
; ,
, 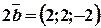 ;
; ,
,  .
. .
. ,.
,.  , поділений точкою М у відношенні
, поділений точкою М у відношенні  . Знайти координати точки М.
. Знайти координати точки М. ;
;  ;
; .
. .
. і
і  , ділиться в точці М навпіл. Знайдіть довжину відрізка МК, де
, ділиться в точці М навпіл. Знайдіть довжину відрізка МК, де  .
. ;
; 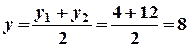 ;
;  ;
; .
. ,
,  .
. .
. ,
,  ,
,  є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D.
є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D.
 , тоді
, тоді  ,
,  . Оскільки
. Оскільки  , їх координати рівні:
, їх координати рівні: ;
;  ;
;  ;
; ;
;  ;
;  .
. .
. та його довжину
та його довжину  .
. ;
;  ;
;  .
. ;
;  ;
;  .
. .
. ,
,  ,
,  . Знайти довжини векторів 1)
. Знайти довжини векторів 1)  , 2)
, 2)  .
. ,
,  ,
,  є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D, а також периметр паралелограму.
є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D, а також периметр паралелограму. ,
,  , кути між віссю l дорівнюють 600 і 1200. Обчислити
, кути між віссю l дорівнюють 600 і 1200. Обчислити  .
.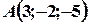 і
і  . Знайти довжину вектора
. Знайти довжину вектора  .
.
 ,
,  , то скалярний добуток обчислюють за формулою:
, то скалярний добуток обчислюють за формулою: .
. .
. .
. .
. .
. , який задовольняє умові:
, який задовольняє умові: ;
; ,
,  ;
;
 . За визначенням випливає, що
. За визначенням випливає, що  .
. .
. .
. .
. (або
(або  ).
).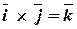 ;
;  ;
;  ;
; ;
;  ;
;  .
. .
.


