
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дотична площина та нормаль поверхні.Содержание книги
Поиск на нашем сайте
Нехай Площина D, що проходить через точку Р, паралельно до Оскільки поверхня регулярна, то дотична площина визначена в будь-якій її точці (як було показано у попередньому параграфі). Дотична у точці P будь-якої кривої, що лежить на поверхні 1. Припустимо, що поверхня Оскільки дотична площина проходить через точку P паралельно векторам Знайдемо рівняння нормалі поверхні
Тоді канонічне рівняння нормалі:
2. Припустимо поверхня задана неявним рівнянням:
де Оскільки вектор Як було показано раніше, усі ці дотичні лежать у дотичній площині поверхні Нехай P має декартові координати
А канонічне рівняння нормалі має вигляд:
Перша квадратична форма регулярної поверхні Нехай
Скалярний квадрат – це: Знайдемо коефіцієнти цієї квадратичної форми. Підставляючи (1), (2), маємо:
Таким чином
Відмітимо, що взагалі коефіцієнти
Відмітимо, що крім позначення (2) для Формули для обчислення коефіцієнтів I(d) 1. Припустимо, що поверхня задана параметричним рівнянням:
Тоді частинні похідні мають координати
2. Припустимо, що поверхня задана явною функцією:
Тоді за формулами (3) маємо:
3. Припустимо, що поверхня задана неявним рівнянням:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.62.198 (0.008 с.) |

 – регулярна поверхня з вектор-функцією
– регулярна поверхня з вектор-функцією  , P є
, P є  не є паралельними.
не є паралельними.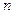 , що проходить через точку P є
, що проходить через точку P є 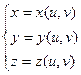 . Припустимо, що точка P має криволінійні координати
. Припустимо, що точка P має криволінійні координати  і декартові координати
і декартові координати  , координати частинних похідних вектор-функції:
, координати частинних похідних вектор-функції:  (1).
(1). .
. , перпендикулярний
, перпендикулярний  , тобто перпендикулярний до дотичної площини D у точці Р. Тому цей вектор є вектором нормалі поверхні
, тобто перпендикулярний до дотичної площини D у точці Р. Тому цей вектор є вектором нормалі поверхні  .
. .
. ,
, 
 . Оскільки
. Оскільки 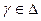 , то має місце тотожність
, то має місце тотожність  . Продиференціюємо цю тотожність:
. Продиференціюємо цю тотожність: (2)
(2) – значення параметру, що відповідає точці Р. Вектор
– значення параметру, що відповідає точці Р. Вектор  називається градієнтом поверхні
називається градієнтом поверхні  є направляючим вектором дотичної кривої
є направляючим вектором дотичної кривої 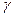 у точці Р, то рівняння (2) показує, що скалярний добуток градієнта і вектора дотичної дорівнює нулю. Тобто градієнт є ортогональним до дотичної будь-якої кривої у точці Р, що лежить на поверхні
у точці Р, то рівняння (2) показує, що скалярний добуток градієнта і вектора дотичної дорівнює нулю. Тобто градієнт є ортогональним до дотичної будь-якої кривої у точці Р, що лежить на поверхні 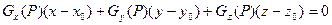 .
. .
. , тоді диференціал вектор-функції
, тоді диференціал вектор-функції  (1), де
(1), де  – частинні похідні,
– частинні похідні,  – довільні дійсні числа, що можуть приймати скільзавгодно малі значення.
– довільні дійсні числа, що можуть приймати скільзавгодно малі значення. (2) називається першою квадратичною формою поверхні
(2) називається першою квадратичною формою поверхні  .
. дійсно квадратична форма від змінних
дійсно квадратична форма від змінних  .
. , а це можливо тільки коли
, а це можливо тільки коли  , оскільки
, оскільки  .
. . Розглядають також
. Розглядають також  . Крім того, будують
. Крім того, будують  .
.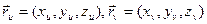 . Тоді
. Тоді (3)
(3) . Тоді
. Тоді
 .
.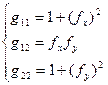 (4)
(4) не дорівнює нулю. Припустимо, що у точці, де розглядається
не дорівнює нулю. Припустимо, що у точці, де розглядається  . Тоді згідно теореми про неявну функцію у деякому околі цієї точки поверхню можна задати явною функцією
. Тоді згідно теореми про неявну функцію у деякому околі цієї точки поверхню можна задати явною функцією 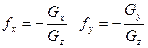 . Тоді з формули (4) отримаємо:
. Тоді з формули (4) отримаємо: (5)
(5)


