
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Головні кривини. Середня і повна кривина.Содержание книги
Поиск на нашем сайте
Нехай Позначимо головні кривини у точці М через Знайдемо формули для обчислення головних, середніх та повних кривин. Припустимо, що
Отримали систему для знаходження головного напрямку
Отримали рівняння для знаходження
Таким же чином можна отримати таке ж саме рівняння для розрахунку
З теореми Вієта:
А повна кривина за теоремою Вієта:
Формули Ейлера. Нехай
Знайдемо зв'язок між головними кривинами поверхні
Оскільки усі точки поверхні крім М у деякому її околі лежать під дотичною площиною П, то точка М є точкою екстремуму для функції (1), оскільки значення цієї функції за модулем – це відстань від площини до поверхні. За критерієм точки екстремуму:
Таким чином
Оскільки напрямки
Припустимо, що напрямку
Оскільки
Оскільки головні напрямки відповідають кутам
Звідси знаходимо значення коефіцієнтів
Вона виражає значення нормальної кривини Дериваційні формули. Нехай Дериваційні формули виражають похідні вектор-функцій
Рівняння (2), (3) називаються дериваційними формулами. Ці формули виражають похідні другого порядку функції Причому рівняння (2), (3) виконуються у кожній точці поверхні з координатами
Покажемо, що коефіцієнти дериваційних формул залежать тільки від коефіцієнтів
Тоді помноживши скалярно обидві частини рівнянь (3) на вектор
Таким чином (3) приймає вигляд:
Помножимо тепер скалярно обидві частини рівнянь (3`) спочатку на вектор
Отримали систему лінійних рівнянь з невідомими
Оскільки розв’язки системи (5) виражаються через коефіцієнти Помножимо скалярно рівняння системи (2) на вектор
Покажемо тепер, що коефіцієнти
Помножимо тепер скалярно рівняння (2) спочатку на вектор
Отримали систему лінійних рівнянь (7) відносно невідомих
Звідси,
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.44.232 (0.007 с.) |

 – регулярна поверхня, М – деяка її фіксована точка,
– регулярна поверхня, М – деяка її фіксована точка,  – вектор-функція поверхні
– вектор-функція поверхні  (не плутати з кривиною та скрутом). Тоді площина
(не плутати з кривиною та скрутом). Тоді площина  називається середньою кривиною поверхні
називається середньою кривиною поверхні 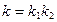 називається повною кривиною поверхні
називається повною кривиною поверхні  головна кривина поверхні
головна кривина поверхні  з точки М. Тоді згідно формули для обчислення нормальної кривини точка
з точки М. Тоді згідно формули для обчислення нормальної кривини точка  має окіл, для кожної точки якого має місце рівняння:
має окіл, для кожної точки якого має місце рівняння:  . Тоді
. Тоді  для усіх точок
для усіх точок  з деякого околу точки
з деякого околу точки  . Згідно критерію точки екстремуму функції декількох змінних, маємо:
. Згідно критерію точки екстремуму функції декількох змінних, маємо:  . Знайдемо ці частинні похідні:
. Знайдемо ці частинні похідні:
 (1)
(1) (2)
(2)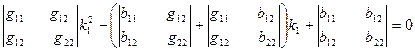 (3)
(3) , тобто
, тобто  (4)
(4) і ми маємо:
і ми маємо: .
. .
.
 є головними. З розділу «Різні аналітичні засоби задання регулярних поверхонь» відомо, що у деякому околі точки М поверхню
є головними. З розділу «Різні аналітичні засоби задання регулярних поверхонь» відомо, що у деякому околі точки М поверхню  (1)
(1) . Тоді згідно формул для коефіцієнтів
. Тоді згідно формул для коефіцієнтів  , коли поверхня задана явною функцією, маємо:
, коли поверхня задана явною функцією, маємо:
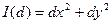 (2)
(2) , тобто
, тобто  . Підставляючи у це рівняння
. Підставляючи у це рівняння  , отримаємо, що
, отримаємо, що  (3)
(3) відповідає головна кривина
відповідає головна кривина  кут між віссю Ох і довільним напрямком
кут між віссю Ох і довільним напрямком  з точки М. Тоді цей напрямок однозначно визначається кутом
з точки М. Тоді цей напрямок однозначно визначається кутом  нормальну кривину у точці М у напрямку
нормальну кривину у точці М у напрямку  (4)
(4)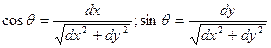 , то рівняння (4) приймає вигляд:
, то рівняння (4) приймає вигляд: (5)
(5) , то з (5) знаходимо значення головних кривин:
, то з (5) знаходимо значення головних кривин:
 . Підставляючи ці значення у (5) отримаємо формулу Ейлера:
. Підставляючи ці значення у (5) отримаємо формулу Ейлера:
 у довільному напрямку
у довільному напрямку  – одиничний вектор головної нормалі поверхні
– одиничний вектор головної нормалі поверхні  .
. через перші частинні похідні функції
через перші частинні похідні функції  . Зафіксуємо точку М на поверхні
. Зафіксуємо точку М на поверхні  не є паралельними. Крім того у цій точці
не є паралельними. Крім того у цій точці  (умови (1)). Звідси випливає, що
(умови (1)). Звідси випливає, що  не компланарні. Тому у кожній точці М поверхні існує система координат з початком в М і базисними векторами
не компланарні. Тому у кожній точці М поверхні існує система координат з початком в М і базисними векторами 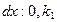 . Тоді похідні вектор-функцій
. Тоді похідні вектор-функцій  (2)
(2) (3)
(3) . Коефіцієнти цих лінійних виразів
. Коефіцієнти цих лінійних виразів  називаються коефіцієнтами дериваційних формул. Зауважимо, що ці коефіцієнти також є функціями від
називаються коефіцієнтами дериваційних формул. Зауважимо, що ці коефіцієнти також є функціями від 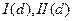 . Причому коефіцієнти
. Причому коефіцієнти 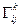 залежать тільки від
залежать тільки від  , то
, то (4)
(4) з урахуванням співвідношень (1), отримаємо:
з урахуванням співвідношень (1), отримаємо: .
. (3`)
(3`) , а потім на вектор
, а потім на вектор  :
:
 , коефіцієнтами якої є коефіцієнти квадратичних форм. Тобто цю систему можна записати в вигляді:
, коефіцієнтами якої є коефіцієнти квадратичних форм. Тобто цю систему можна записати в вигляді: (5)
(5)
 залежать тільки від коефіцієнтів
залежать тільки від коефіцієнтів  (6)
(6) (7)
(7) (8)
(8)


