
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Довжина дуги кривої на поверхніСодержание книги
Поиск на нашем сайте
Нехай
Довжина дуги кривої
Підставляючи (1) в (2) маємо:
З формули для обчислення довжини дуги кривої на поверхня випливає, що диференціал довжини дуги кривої на поверхні має вигляд:
Кут між кривими на поверхні Нехай Нехай
Ці вирази отримані за правилами обчислення скалярних добутків з урахуванням того, що Підставляючи (2), (3), (4) в (1) отримаємо формулу для обчислення кута між кривими на поверхні
Оскільки криволінійні координати
Підставляючи ці значення у (5), після скорочень у чисельнику та знаменнику маємо: Через кожну точку P поверхні
Підставляючи отримані значення у (5), маємо:
Площа простого шматка регулярної поверхні Нехай
Позначимо площі плоских паралелограмів
За означенням площі шматка поверхні П: Покажемо, що у випадку регулярної поверхні границя (3) існує і знайдемо формули для її обчислення. Згідно формули ряду Тейлора:
Підставляємо (4) в (2), отримаємо:
Використовуючи лінійності векторного добутку, отримаємо:
де Оскільки для будь-яких векторів
Ця нескінченно мала функція є сумою нескінченно малих, звідси:
Підсумувавши
Припустимо, що має місце твердження:
З урахуванням припущення ми бачимо, що
де С – площа прямокутника, який вписано в G. Оскільки Таким чином
Залишилось довести тільки припущення (*). Враховуючи (8), нам достатньо довести що
З (7) випливає:
Тому достатньо довести, що виконується твердження:
де Розглянемо це твердження для першого доданку:
Оскільки
Таким чином нам достатньо довести наступне твердження:
Розглянемо співвідношення (4):
Згідно теореми про середнє значення регулярної функції:
Отримаємо:
Оскільки функція
Тоді з (11) випливає
Теорема: Нехай
де Доведення: Згідно формули (9) нам достатньо довести, що
Згідно формули для обчислення векторного добутку маємо, що
Тоді за формулою (9):
Наслідок: Нехай поверхня
Доведення: За формулою (13) нам достатньо довести, що
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.131.64 (0.007 с.) |

 – поверхня,
– поверхня,  – її вектор-функція,
– її вектор-функція,  – крива, що лежить на поверхні.
– крива, що лежить на поверхні.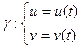 – внутрішнє рівняння кривої
– внутрішнє рівняння кривої 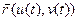 (1).
(1).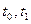 обчислюється за формулою:
обчислюється за формулою: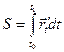 (2).
(2).
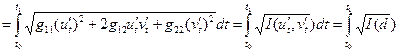 .
.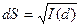 .
. і
і  проходять через точку Р. Кутом між кривими
проходять через точку Р. Кутом між кривими  та
та 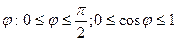 .
.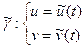 – внутрішні рівняння
– внутрішні рівняння 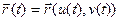 – вектор-функція кривої
– вектор-функція кривої  – вектор-функція кривої
– вектор-функція кривої 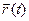 ,
,  – напрямні вектори. Припустимо, що значенню параметра
– напрямні вектори. Припустимо, що значенню параметра 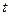 відповідає точка:
відповідає точка:  . Оскільки
. Оскільки 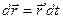 , тобто диференціал вектор-функції і її похідна є колінеарними векторами, то
, тобто диференціал вектор-функції і її похідна є колінеарними векторами, то (1)
(1)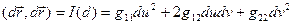 (2)
(2)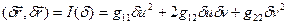 (3)
(3)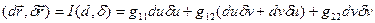 (4)
(4)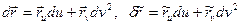 .
.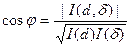 (5)
(5)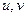 у вектор-функції (5) відповідають точкам кривих
у вектор-функції (5) відповідають точкам кривих 

 .
. . Знайдемо кут між ними. Підставляючи формули у (2), (3), (4), маємо:
. Знайдемо кут між ними. Підставляючи формули у (2), (3), (4), маємо: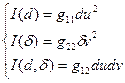 .
. – для координатних ліній. Звідси, координатні лінії в точці P є перпендикулярними тоді і тільки тоді, коли у цій точці
– для координатних ліній. Звідси, координатні лінії в точці P є перпендикулярними тоді і тільки тоді, коли у цій точці 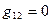 .
. . Оскільки G є обмеженою, то її можна вписати у деякий прямокутник. Цей прямокутник можна розбити на менші прямокутники з довжиною сторін
. Оскільки G є обмеженою, то її можна вписати у деякий прямокутник. Цей прямокутник можна розбити на менші прямокутники з довжиною сторін  . Ці прямокутники відобразяться у криволінійні паралелограми. Нехай точка P – вершина паралелограма. Нехай
. Ці прямокутники відобразяться у криволінійні паралелограми. Нехай точка P – вершина паралелограма. Нехай  . Тоді ближнім вершинам будуть відповідати вектори
. Тоді ближнім вершинам будуть відповідати вектори  . Розглянемо плоский паралелограм з цими вершинами, він буде побудований на векторах:
. Розглянемо плоский паралелограм з цими вершинами, він буде побудований на векторах: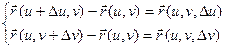 (1)
(1) (2)
(2)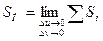 (3)
(3)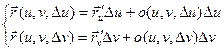 (4)
(4) (5)
(5)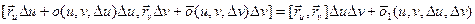 (6)
(6)
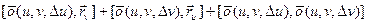 (7)
(7)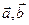 виконується нерівність
виконується нерівність 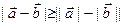 , то з (6), з урахуванням рівності (5) випливає:
, то з (6), з урахуванням рівності (5) випливає:
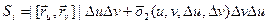
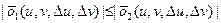 (8)
(8) отримаємо за означенням:
отримаємо за означенням: .
.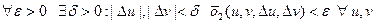 (*)
(*)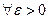 існує таке розбиття області G, таке що
існує таке розбиття області G, таке що 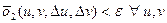 . Тому
. Тому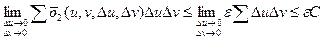 ,
,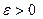 – скільзавгодно мале число, то
– скільзавгодно мале число, то 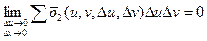 .
.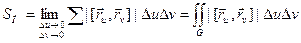 . (9)
. (9)
 (10)
(10)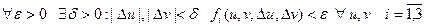 ,
, – доданки з правої частини нерівності (10).
– доданки з правої частини нерівності (10). .
. – неперервний на обмеженій замкненій множині
– неперервний на обмеженій замкненій множині 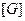 , тому
, тому  .
.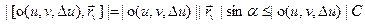 .
. .
.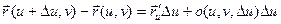 .
.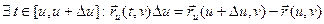 .
.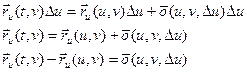
 неперервна на замкненій обмеженій множині
неперервна на замкненій обмеженій множині 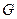 . А це означає, що
. А це означає, що (11)
(11) . Тим самим твердження повністю доведено.
. Тим самим твердження повністю доведено. (12)
(12)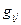 – коефіцієнти I квадратичної форми.
– коефіцієнти I квадратичної форми. (13)
(13)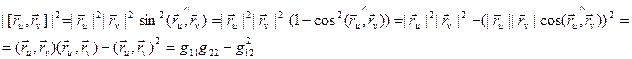
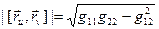 .
.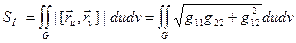 .
. , П – простий шматок поверхні
, П – простий шматок поверхні  . Тоді площа шматка П:
. Тоді площа шматка П: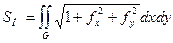 .
.

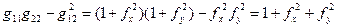
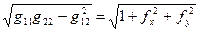 .
.


