
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Явища переносу в газах. Рівняння переносу.Содержание книги
Поиск на нашем сайте
Хаотичний рух молекул газу веде до безперервного перемішування газу. З цим пов’язаний ряд важливих явищ, що відбуваються в газах. Якщо в різних частинах об’єму газу густина була спочатку неоднаковою, то з часом вона вирівнюється. Також, якщо два різних гази дотикаються, то вони рівномірно перемішуються між собою. Це явище називається дифузією. Дифузія – розповсюдження речовини в деякому середовищі в напрямі зменшення її концентрації, зумовлене тепловим рухом атомів, молекул, іонів і інших більш великих частинок. В об’ємі газу, частини якого мають різну температуру, відбувається поступове вирівнювання температури внаслідок переносу молекулами своєї енергії. Це явище називається теплопровідністю. Теплопровідність – один з видів теплообміну, при якому перенесення енергії в формі теплоти в нерівномірно нагрітому середовищі має атомно-молекулярний характер (не пов’язаний з макроскопічним рухом речовини). В’язкість (внутрішнє тертя) рідин і газів - властивість рідин і газів чинити опір переміщенню однієї їх частини відносно іншої. Всі вище названі явища зумовлені однією причиною – переносом молекулами газу в процесі хаотичного руху своїх характеристик: маси – дифузія енергія - теплопровідність імпульсу руху – внутрішнє тертя (в’язкість) Тому механізм всіх цих явищ однаковий і всі вони об’єднані спільною назвою явищ переносу. Виходячи з уявлень МКТ виведемо загальне для явищ переносу рівняння переносу. З цією метою визначимо перш за все кількість молекул, що проходять за проміжок часу dt крізь деяку уявну площадку dS, розміщену в газі (мал.1).
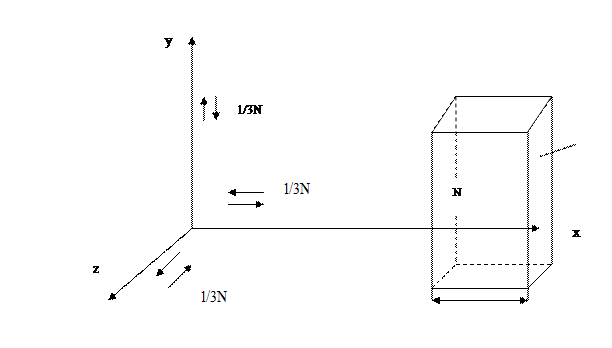
Мал.1 Внаслідок хаотичного руху молекул припустимо, що вздовж кожної з осей рухається 1/3 частина всіх молекул:тому 1/6 частина – зліва направо і 1/6 частина – справа наліво. Тоді за одиницю часу крізь площадку dS пройде зліва направо 1/6 частина всіх молекул, що знаходяться в об’ємі прямокутного паралелепіпеду з основою dS і висотою, що дорівнює середній швидкості
де Отже, кількість молекул N, що проходять крізь площадку
Ці молекули переносять крізь площадку Розглядаючи загальний механізм переносу, поки що не будемо конкретизувати, яку саме фізичну характеристику переносять молекули і позначимо її
Очевидно, що така ж кількість буде перенесена в зворотному напрямі. Припустимо тепер, що газ неоднорідний за своїми властивостями, тобто концентрація n його різна в різних місцях об’єму газу і самі молекули мають неоднакові значення фізичної величини
мал.2 Згідно формулі (1) воно дорівнює:
Залишається вияснити, виходячи з фізичних уявлень, на якій відстані від площадки dS слід взяти значення
Як видно з мал. відношення
Знак „мінус” зумовлений тим, що перенесення фізичної величини відбувається в напрямі протилежному градієнту (градієнт Формула (4) називається рівнянням переносу. На основі цього рівняння розглянемо конкретні явища переносу: дифузію, теплопровідність, внутрішнє тертя.
Дифузія.
Нехай в деякому об’ємі газу має місце неоднорідність густини. Густина
Це може бути, наприклад, у випадку, коли в лівій частині об’єму знаходиться джерело газу О (рідина, що випаровується). Позначимо через Тоді
де де Dm – маса газу, що переноситься шляхом дифузії за час dt крізь площадку dS, перпендикулярну напряму зменшення густини. Підставивши вираз (5) в рівняння переносу (4), одержимо:
Позначивши D= Отримаємо Звідки слідує, що маса газу dM, що переноситься завдяки дифузії крізь площадку dS, перпендикулярну до напряму осі Ох в якому зменшується густина, пропорційна розміру цієї площадки, проміжку часу dT переносу і градієнту густини Формула (8) називається рівнянням дифузії чи законом Фіка, бо німецький фізик Фік отримав таке ж рівняння з дослідів з рідинами. Коефіцієнт пропорційності D називається коефіцієнтом дифузії. Встановимо фізичний зміст коефіцієнта дифузії D, вважаючи в формулі (8) dS=1м2 Dt=1c, З формули (7) і (8) слідує, що коефіцієнт дифузії вимірюється в
Теплопровідність.
Нехай в деякому об’ємі газу Т температура зменшується у напрямі осі Ох (мал.4)
Це може мати місце, наприклад, у випадку, коли в лівій частині в т.О об’єму знаходиться нагрівач. Позначимо через Т1 і Т2 - значення температури на відстані
де і – число ступенів вільності молекули. З цієї формули слідує, що Е1 > Е2, тобто енергія молекул, що знаходиться зліва від dS більша, за енергію молекул, що знаходиться справа від dS. Тому в напрямі зменшення температури буде відбуватися переважне перенесення енергії, а отже, і кількість теплоти dQ, бо внутрішня енергія газу складається з кінетичної енергії його молекул. Застосовуючи рівняння переносу (4), відмітимо, що в даному випадку фізичною характеристикою, що переноситься, є енергія молекули, тобто Тоді, так як концентрацію n молекул можна вважати однаковою у всьому об’ємі газу, можемо записати:
де dT = Т1 - Т2
де dQ – кількість теплоти (внутрішня енергія), що переноситься за час dT крізь площадку dS, перпендикулярну напряму зменшення температури. Підставляючи вираз (9) і (10) в рівняння переносу (4) отримаємо
Помноживши і поділивши праву частину цієї рівності на масу молекули m і врахувавши, що
де
Тоді останню рівність можна записати в такому вигляді:
Тоді отримаємо:
Позначимо
де
З формули (13) слідує, що кількість теплоти dQ, що переноситься крізь площадку dS, перпендикулярну до напряму осі Ох, в якому зменшується температура, пропорційна розмірам цієї площадки, проміжку часу dt переносу і градієнту температури Формула (13) називається рівнянням теплопровідності чи законом Фур’є (бо вперше це рівняння вивів французький математик Фур’є). Вияснимо фізичний зміст коефіцієнта теплопровідності
Тоді отримаємо: З формул (12) і (13) слідує, що коефіцієнт теплопровідності вимірюється в
Внутрішнє тертя(в’язкість).
Нехай в ламінарному (такому, що встановився) потоці газу швидкість течії зменшується в напрямку осі Ох.
Уявімо площадку dS, вздовж якої дотикаються 2 сусідні шари газу і позначимо через В результаті цього між шарами виникає внутрішнє тертя, сила якого буде діяти вздовж площадки dS паралельно швидкості потоку. Застосувавши рівняння переносу (4), відмітивши, що в цьому випадку фізичною характеристикою, що переноситься, є імпульс руху молекул:
Тоді, так як концентрацію молекул n можна вважати однаковою у всьому об’ємі газу, можемо записати, що де
де
Підставивши вирази (14) і (16) в рівняння (4), отримаємо:
Тоді З формули (19) слідує, що: сила внутрішнього тертя, що виникає в площині дотику двох шарів газу, які ковзають один відносно одного, пропорційна площі їх дотику dS і градієнту швидкості Формула (19) називається рівнянням внутрішнього тертя, чи законом Ньютона, бо Ньютон отримав таке ж рівняння з дослідів з рідинами. Коефіцієнт пропорційності Вияснимо його фізичний зміст, скориставшись формулою (9), в якій будемо вважати dS =1m2, а
З формули (18) і (19) слідує, що коефіцієнт внутрішнього тертя вимірюється в Д=
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1095; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |



 - кількість молекул в одиниці об’єму газу (концентрація молекул).
- кількість молекул в одиниці об’єму газу (концентрація молекул). за час dt в одному напрямі, визначається формулою
за час dt в одному напрямі, визначається формулою
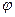 .Тоді кількість фізичної характеристики, перенесеної молекулами в одному напрямі крізь площадку
.Тоді кількість фізичної характеристики, перенесеної молекулами в одному напрямі крізь площадку  (1)
(1) , що міститься в одиниці об’єму газу також буде різною в різних місцях об’єму газу. Нехай кількість
, що міститься в одиниці об’єму газу також буде різною в різних місцях об’єму газу. Нехай кількість  крізь площадку dS зліва направо (мал..2)
крізь площадку dS зліва направо (мал..2)
 (2)
(2)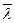 , що дорівнює середній довжині вільного пробігу молекули. Тому, можна припустити, що значення величини
, що дорівнює середній довжині вільного пробігу молекули. Тому, можна припустити, що значення величини  (3)
(3) є градієнтом величини
є градієнтом величини  , який ми позначимо символом
, який ми позначимо символом  . Градієнтом фізичної величини називається її зміна, що припадає на одиницю відстані в напрямі найбільшого збільшення. Отже, градієнт є вектор, направлений в бік найбільшого зростання фізичної величини. Тоді формула (3) прийме вид:
. Градієнтом фізичної величини називається її зміна, що припадає на одиницю відстані в напрямі найбільшого збільшення. Отже, градієнт є вектор, направлений в бік найбільшого зростання фізичної величини. Тоді формула (3) прийме вид: (4)
(4) зменшується в напрямі осі Ох (мал.3)
зменшується в напрямі осі Ох (мал.3)
 , де
, де 
 і
і  значення густини на відстані
значення густини на відстані  (за значенням), де m – маса молекули, однакова для всіх молекул газу, але
(за значенням), де m – маса молекули, однакова для всіх молекул газу, але  , тобто концентрація молекул зменшується в напрямі осі Ох разом з густиною. Застосуємо рівняння переносу (4). Відмітимо, що в даному випадку фізичною характеристикою, що переноситься, є маса молекул, тобто
, тобто концентрація молекул зменшується в напрямі осі Ох разом з густиною. Застосуємо рівняння переносу (4). Відмітимо, що в даному випадку фізичною характеристикою, що переноситься, є маса молекул, тобто тому
тому  (5),
(5), (5)
(5)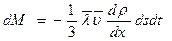 (6)
(6) (7)
(7) (8)
(8) .
. .
.

 .
. (9)
(9) (9)
(9) (10)
(10)
 можемо записати
можемо записати
 ,
,  ,
,  ,
,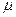 - молярна маса
- молярна маса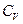 - молярна теплоємність газу при V=const
- молярна теплоємність газу при V=const
 - питома теплоємність газу при V=const
- питома теплоємність газу при V=const (11)
(11) (12)
(12) - коефіцієнт теплопровідності
- коефіцієнт теплопровідності (13)
(13) .
.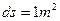 ,
, 

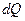 , тобто коефіцієнт теплопровідності чисельно дорівнює кількості теплоти, що переноситься крізь площадку в 1м2 за 1с. при градієнті температури в
, тобто коефіцієнт теплопровідності чисельно дорівнює кількості теплоти, що переноситься крізь площадку в 1м2 за 1с. при градієнті температури в  .
.

 , де k- імпульс руху
, де k- імпульс руху і
і  значення швидкостей на відстанях
значення швидкостей на відстанях  , внаслідок чого швидкість молекул верхнього шару приведе то того, що вони будуть мати більший імпульс руху, ніж молекули нижнього шару, тобто
, внаслідок чого швидкість молекул верхнього шару приведе то того, що вони будуть мати більший імпульс руху, ніж молекули нижнього шару, тобто  >
>  , де m – маса молекули. В процесі хаотичного руху молекули верхнього шару будуть переносити свій імпульс руху в нижній шар, збільшуючи його швидкість.
, де m – маса молекули. В процесі хаотичного руху молекули верхнього шару будуть переносити свій імпульс руху в нижній шар, збільшуючи його швидкість.
 (14)
(14)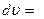
 (15)
(15) - зміна імпульсу руху одного шару відносно іншого, що відбувається за час dt на площадці dS, бо зміна імпульсу руху за ІІ законом Ньютона дорівнює імпульсу діючої сили, тобто
- зміна імпульсу руху одного шару відносно іншого, що відбувається за час dt на площадці dS, бо зміна імпульсу руху за ІІ законом Ньютона дорівнює імпульсу діючої сили, тобто  , де F – сила взаємодії між шарами газу, що діє в площині їх дотику, тобто сила внутрішнього тертя. Тому формулу (15) можна записати у вигляді:
, де F – сила взаємодії між шарами газу, що діє в площині їх дотику, тобто сила внутрішнього тертя. Тому формулу (15) можна записати у вигляді: (16)
(16) (17)
(17)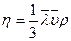 (18)
(18) (19)
(19) .
.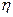 називається коефіцієнтом внутрішнього тертя або в’язкості.
називається коефіцієнтом внутрішнього тертя або в’язкості. . На завершення підкреслимо, що зіставляючи формули
. На завершення підкреслимо, що зіставляючи формули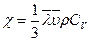 і
і  , які також знаходяться у відповідності з дослідними даними. Це є додатковим підтвердженням вірності розглянутої нами МКТ будови речовини.
, які також знаходяться у відповідності з дослідними даними. Це є додатковим підтвердженням вірності розглянутої нами МКТ будови речовини.


