
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 1. Основи кінематики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Частина 1. Механіка. Вступ: Механіка – фундаментальна фізична теорія, що встановлює закономірності взаємних переміщень тіл в просторі і взаємодій, що відбуваються при цьому. Механіка, як наука сформувалась з виходом книги І. Ньютона „Математичні начала натуральної філософії (1687). Ньютон зібрав і опрацював весь накопичений матеріал, систематизував його, багато доповнив. Створена Ньютоном механіка називається класичною. Класична механіка вивчає рух макроскопічних тіл, які є матеріальними точками і рухається зі швидкостями значно меншими швидкості світла(
В 1905 р. з’явилась перша робота А Ейнштейна, яка поклала початок релятивістської механіки (СТВ). Але формули СТВ використовуються тільки тоді, коли доводиться вивчати рух тіл, швидкість яких не небагато менша швидкості світла. Взагалі швидкість світла є граничною швидкістю передачі сигналу(взаємодій) і є фундаментальною константою. Механіка розв’язує два основних завдання: 1. Вивчення різноманітних рухів і узагальнення одержаних результатів у вигляді законів, руху – законів, за допомогою яких можна передбачити характер руху в кожному конкретному випадку. 2. Пошук загальних властивостей притаманних будь-якій системі, незалежно від конкретного виду взаємодії між тілами системи. Розв’язок першої задачі привів до встановлення І. Ньютоном динамічних законів, в той час як розв’язок ІІ задачі – до виявлення законів збереження таких величин, як енергія, імпульс і момент імпульсу. Під механічним рухом розуміють зміну положення тіл або частин тіл відносно інших тіл в просторі з часом.
Розділ 1. Основи кінематики. Основні поняття кінематики.
Кінематика – вивчає рух тіла відносно інших тіл незалежно від причин(сил), що впливають на цей рух. Пряма основна задача кінематики – полягає в знаходженні любого параметра руху за відомим законом руху. Вона розв’язується шляхом послідовного застосування основних законів кінематики(руху, швидкості і прискорення). Обернена задача кінематики – полягає у визначенні закону руху за яким-небудь відомим параметром руху(вектор швидкості чи вектор прискорення). В загальному випадку обернена задача значно складніша, ніж пряма. Механічний рух зручно вивчати на прикладі ідеального об’єкту – матеріальної точки. Матеріальна точка – макроскопічне тіло, розміром і внутрішньою структурою якого можна знехтувати за даних умов руху і вважати, що вся речовина тіла начебто зосереджена в одній геометричній точці. На відміну від геометричної точки, матеріальна точка володіє здатністю взаємодіяти з іншими тілами і їй приписується деяка маса. Питання про те, чи можна конкретне тіло розглядати, як матеріальну точку визначається не розмірами самого тіла, а умовами руху, що розглядається. Тому одне і те ж тіло в одних випадках, можна вважати матеріальною точкою, а в інших – ні. Наприклад, при русі Землі по орбіті навколо Сонця її можна вважати матеріальною точкою(діаметр Землі – 12740 км, відстані від Землі до Сонця – 150 млн. км), а при вивченні обертального руху Землі навколо осі – ні. В означення матеріальної точки введено умову, що тіло повинно бути макроскопічним. Це пов’язано з тим, що при русі макроскопічних тіл, таких як атоми, молекули і елементарні частинки суттєво проявляються хвильові властивості. Рух таких об’єктів описується вже законами квантової механіки. Слід зазначити, що наближення матеріальної точки працює і тоді, коли рух тіл кінцевих розмірів є поступальним(тобто довільний відрізок, що сполучає любі дві точки тіла, залишається в просторі паралельним собі). Знати рух матеріальної точки означає вміти в будь-який момент часу визначити її положення в просторі, якщо відомі початкові умови руху. Траєкторія – лінія вздовж якої рухається матеріальна точка. Тіло відносно якого розглядається механічний рух називається тіло відліку. Дослід показує, що для повного завдання положення матеріальної точки в просторі відносно тіла відліку, необхідно задати три координати точки. Частіше з обраним тілом відліку зв’язують декартову систему координат, тоді положення матеріальної точки в просторі задають за допомогою радіус-вектора
мал.1
Система відліку – це тіло відліку, пов’язана з ним система координат і прилад для вимірювання проміжків часу. Використовується для визначення положення в просторі досліджених фізичних об’єктів (тіл, частинок) в різні моменти часу. При цьому тіло відліку і годинник вважаються нерухомими. Системи відліку можна зв’язувати з різними тілами, але особливо важливим є клас так званих вільних тіл. Вільним тілом називається тіло настільки віддалене від інших тіл, що їх дією на це тіло можна знехтувати. Система відліку пов’язана з вільним тілом називається інерціальною системою відліку(ІСВ). Система відліку, яка не рухома, чи рухається рівномірно прямолінійно відносно даної ІСВ сама є інерціальною. Всі закони фізики мають однаковий вид в будь якій ІСВ. Тому всі ІСВ фізично рівноправні. Рівноправність ІСВ відображає властивості симетрії простору-часу – його ізотропність і однорідність. Фізичні величини поділяються на скалярні і векторні величини. Скалярною називається фізична величина, що характеризується числовим значенням, яке не змінюється при перенесені системи координат чи зміні початку відліку часу(маса, шлях, температура, густина і т.п.) Векторною називають величину, що характеризується числовим значенням, напрямом простору і що додається з іншою собі подібною величиною геометрично(за правилом паралелограма). При русі матеріальної точки її положення в просторі змінюється. Відповідно цьому радіус-вектор матеріальної точки можна розглядати як функцію часу
Векторна функція (1) рівносильна заданню трьох скалярних функцій:
Шлях – це довжина траєкторії, яке проходить тіло за даний проміжок часу. Переміщення – вектор, що сполучає початкове та кінцеве положення тіла. Швидкістю називається векторно-фізична величина, що дорівнює першій похідній переміщення по часу.
Прискоренням називається векторна фізична величина, що дорівнює похідній вектора швидкості по часу.
Рух по колу.
Кутом повороту називається кут утворений радіус-вектором, що сполучає початкове і кінцеве положення матеріальної точки і центр кола. Вимірюється Кут в 1 рад – це центральний кут, що вирізує на колі довжину дуги рівну радіусу. Кутовою швидкістю називають похідна кута повороту по часу
При рівномірному русі по колу час протягом якого відбувається один повний оборот матеріальної точки називається періодом обертання Т. Величина, що дорівнює кількості обертів за 1 с називається частотою
Розглянемо частину кола, яку пройшла матеріальна точка за деякий проміжок часу. Вважаємо, що швидкість змінюється за напрямком і величиною. При русі по колу швидкість направлена по дотичній кола.
Якщо тіло рухається по прямолінійній траєкторії, то такий рух називається криволінійним.
Розділ 2. Основи динаміки.
Вступ в динаміку. Динаміка – розділ механіки в якому вивчають закономірності і умови механічного руху макроскопічних тіл під дією прикладених до них сил. В основі динаміки, лежать закони Ньютона, з яких отримують всі рівняння, необхідні для розв’язку практичних задач динаміки. В динаміці розглядають 2 типи задач, розв’язок яких для матеріальної точки(чи тіла, що рухається поступально) знаходяться за допомогою законів Ньютона: Задачі І типу полягають в тому, що знаючи рух тіла, визначити діючі на нього сили. Задачі ІІ типу – за діючими на тіло силами визначити закон його руху. Для розв’язку цих задач необхідно знати так звані початкові умови руху, тобто положення і швидкість руху тіла на початку його руху під дією заданих сил.
Закони руху Ньютона.
Перший закон Ньютона.
Якщо на тіло не діють інші тіла, або якщо їх дія взаємно скомпенсовані, то тіло зберігає стан спокою чи рівномірного прямолінійного руху. Ця властивість тіл називається інерцією. Головна думка І закону Ньютона полягає в тому, що лише зовнішні сили можуть змінити спокій чи швидкість руху тіла, саме ж тіло, якщо воно „вільне”, володіє інерцією: воно зберігає свій спокій чи прямолінійний рух з постійною швидкістю. Наведемо формулювання І закону за Ньютоном: будь-яке тіло зберігає стан спокою чи рівномірного прямолінійного руху доти і постільки доти дія з боку інших тіл не примушує його змінити цей стан. За допомогою безпосереднього досліду ми не можемо ні підтвердити, ні заперечити І закону механіки, бо в земних умовах важко здійснити дослід, при якому на тіло не діяли б зовнішні сили. Власне кажучи, цей закон справедливий лише для матеріальних точок, бо тіла можуть і не зберігати свого спокою, знаходячись, наприклад, в обертальному русі. Матеріальна ж точка обертатись не може. Для реальних тіл І закону Ньютона виконується тільки у випадку їх поступального руху. В цьому формулюванні І закону не має вказівок на вибір системи відліку, але розуміння, що твердження відноситься до руху чи спокою в певній системі відліку. Без вказівки на систему відліку закон втрачає сенс. Можна, проте, припустити, що існує така система відліку, в якій прискорення матеріальної точки цілком зумовлене тільки її взаємодією з іншими тілами. Вільна матеріальна точка, на яку не діють інші тіла, рухається відносно такої системи відліку прямолінійно або, як кажуть, за інерцією. Таку систему називають інерціальною. Тому сформулюємо І закон Ньютона таким чином: Існують системи відліку, відносно яких тіло зберігає стан спокою чи рівномірного прямолінійного руху, якщо на нього не діють інші тіла чи їх дія скомпенсована. Такі системи відліку називають інерціальними. Іноді стверджують, що при рівномірному і прямолінійному русі тіло рухається за інерцією. Це не слід розуміти так, що тіло рухається внаслідок інерції. Для того, щоб тіло зберегло стан прямолінійного і рівномірного руху, не потрібно ніяких причин. Рівномірний і прямолінійних рух тіла(рух за інерцією) і спокій – це природний стан будь-якого тіла, вільного від зовнішніх дій або якщо дія на нього інших тіл скомпенсована. Отже, інерція – це властивість всіх тіл, що виявляється в інерціальних системах відліку. Полягає вона в тому, що тіла при відсутності зовнішніх дій, зберігають швидкість свого руху незміною(включаючи і частинний випадок спокою). Інерція властива будь-якому тілу, але для неї не вводиться ніякої кількісної міри, тобто інерція є властивістю, що не вимірюється. Межі застосування І закону Ньютона: Застосовний завжди. Але в першому законі Ньютона закладено в неявному вигляді уявлення про однорідність і ізотропність простору і однорідність часу. Ізотропність означає еквівалентність його властивостей у всіх напрямах. Однорідність простору означає однаковість протікання його явищ в різних точках простору за однакових початкових умов.
Маса і сила.
Маса. Розглянемо властивість, притаманну всім тілам, яка на відміну від інерції, має кількісну характеристику. Інертність – теж властивість, і вона також виявляється в ІСВ. Полягає вона в зміні швидкості тіл(в появі прискорення) під дією зовнішніх тіл. При цьому різні тіла по різному змінюють свою швидкість під дією одного і того ж тіла. Інертність – властивість, що вимірюються. Маса і є мірою, кількісною характеристикою цієї властивості. Зазначимо, що взагалі в фізиці маса, може характеризувати і інші властивості тіл: Наприклад, розглянемо такі співвідношення:
В (1) – маса – міра інертності. В (2) – міра інтенсивності гравітаційної взаємодії(гравітаційна маса). В (3) – міра внутрішньої енергії тіл при теплопередачах. В (4) – міра енерговмісту речовини. В механіці маса – це фізична величина, що є мірою інертності і мірою тяжіння матеріальних об’єктів. В принципі, не звідки не слідує, що маса, яка створює поле тяжіння, визначає і інерцію того ж тіла. Але велика сукупність дослідів показала, що інертна і гравітаційна маси пропорційна одна одній і чисельно рівні у вибраній системі одиниць(Сі). Цей фундаментальний закон природи називається принцип еквівалентності. Експериментально принцип еквівалентності встановлений з точністю до Як слідує з досліду, в рамках класичної механіки масі притаманні дві важливі властивості: 1. Маса – величина адитивна, тобто маса тіла дорівнює сумі мас його окремих частин. 2. Маса тіла – величина постійна і не змінюється при його русі(при Маса даного тіла в класичній механіці не залежить від вибору ІСВ. Сила. Сила – векторна величина, що є мірою механічної взаємодії чи дії на матеріальну точку або тіло з боку інших тіл чи полів. Ця взаємодія може здійснюватись як при безпосередньому контакті тіл(тиск, тертя), так і між віддаленими тілами через поле тяжіння(гравітаційне). Сила характеризується числовим значенням(модулем), напрямом в просторі і точкою прикладання. Отже, сила – векторна величина. Якщо на тіло діє кілька сил, то їх дію можна замінити дією однієї сили, яка називається рівнодійною.
Задача знаходження рівнодійної сили за даними складовими, називається додаванням сил. Ця задача завжди розв’язується однозначно.
Задача знаходження складових сил за заданою рівнодійною, називається розкладанням сил. Якщо задана тільки рівнодійна сила, то задача знаходження складових сил є невизначеною, тобто має множину розв’язків.
Для того, задача розкладання рівнодійної сили на складові стала визначеною, необхідно крім рівнодійної, знати напрям однієї з складових
Другий закон Ньютона.
ІІ закон Ньютона: Прискорення, з яким рухається матеріальна точка, прямо пропорційне діючій на матеріальну точку силі і обернено пропорційне масі матеріальній точки.
Межі застосування закону. 1. рух тіла розглядається по відношенню до інерціальних систем відліку. 2. Рухоме тіло повинно бути: a) макроскопічним. b) матеріальною точкою 3. Маса тіла – величина постійна. 4. Швидкість набагато менша за швидкість світла. v<<c. 5. Для випадку таких взаємодій, коли величина і напрям сил не залежать від швидкостей тіл стосовно даної ІСВ. При порушенні хоча б однієї з цих умов ІІ закону Ньютона застосовувати не можна. Самим Ньютоном ІІ закон був сформульований не через прискорення, а через іншу фізичну величину – імпульс руху тіла. Імпульсом тіла називається векторно-фізична величина, що дорівнює добутку маси тіла на його швидкість.
ІІ закон у формулюванні Ньютона: зміна імпульсу руху пропорційна прикладеній силі, що викликає рух і відбувається вздовж тієї ж прямої, по якій ця сила діє. Використовується також формула:
В диференціальній формі:
Висловимо переваги і недоліки формулювань ІІ закону Ньютона, поданих формулами (5) і (7). Формула (5) характерна тим, що зліва наведена кінетична характеристика руху(прискорення), а справа – динамічна характеристика тіла, що рухається. Тобто, цей закон зв’язує між собою два розділи: кінематику і динаміку. Ця формула виражає функціональну залежність, яка полягає в тому, що прискорення прямо пропорційне результуючій силі і обернено пропорційне масі тіла, що рухається. Основний недолік: прискорення в механіці вважається заданої величиною. Тому для практичних цілей вона не годиться. Формула (7) Переваги: 1) вона годиться для розв’язування більшості практичних задач. 2) справа в (7) знаходяться величини, що характеризують саме рухоме тіло, а зліва – величина, що характеризує тіла, які є причиною руху даного тіла. Недолік: ця форма запису може викликати невірне уявлення, що є причиною, а що наслідком для прискорення і сили.
Третій закон Ньютона.
У формулюванні Ньютона цей закон звучить так: 1. Дії завжди є рівна і протилежна протидія. 2. Дії двох тіл одне на одне між собою рівні і направлені в протилежні напрями. Сучасне формулювання ІІ закону Ньютона: Тіла діють одне на одне з силами, направленими вздовж однієї прямої, рівними за модулем і протилежними за напрямом. Математично записується:
Сили мають одну природу, прикладені до різних тіл, а отже вони не можуть бути скомпенсовані. В загальному випадку рівнодійної сил, про які мова йде в ІІІ законі Ньютона, не існує. Однак є один єдиний випадок, коли про рівнодійну можна вести мову в теоретичному плані: якщо система замкнута(ізольована), тобто в ній діють тільки внутрішні сили, то і до таких сил ІІІ закон застосовний.
Фізично це означає, що внутрішні сили не в змозі вивести систему, як таку зі стану спокою. Для того, щоб це відбулося, необхідна наявність зовнішніх сил. ІІІ закон Ньютона забороняє однобічну дію тіл, встановлює обов’язковість двохсторонніх рівних взаємодій тіл(принцип заборони). Відмітимо, що ІІІ закон Ньютона нічого не говорить про те, яким способом здійснюється взаємодія тіл і про величину сил взаємодії, крім того, що вони рівні і протилежні за напрямом в кожний момент часу. Закон збереження імпульсу.
Механічна система називається замкнутою (ізольованою), якщо можна знехтувати дією зовнішніх сил, в порівнянні з внутрішніми силами, що діють в цій системі. Підкреслимо, що поняття замкнутої системи має зміст тільки стосовно ІСВ, бо в неірціальних системах відліку завжди діє сила інерції, що відіграють роль зовнішніх сил. Для Виведення закону збереження імпульсу скористаємося ІІ і ІІІ законами Ньютона, застосувавши їх до замкнутої системи із n тіл. Застосуємо до взаємодії цих тіл вираз ІІ закону Ньютона.
Повний вектор імпульсу замкнутої системи залишається постійною величиною під час всіх процесів і рухів, що відбуваються в системі. Практично частіше використовують закон збереження імпульсу в такому формулюванні: В замкнутій системі векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії.
Приклади: 1) снаряд масою
2) Людина знаходиться в нерухомому човні. Якщо вона почне переміщуватись вздовж човна, то човен прийде в рух в протилежну сторону. Швидкість руху човна можна знайти так як в попередньому випадку.
Механічна робота.
Механічна робота – скалярна фізична величина, що характеризує процес перетворення однієї форми руху в іншу і чисельно дорівнює скалярному добутку сили на переміщення
Формули (1) і (2) справедливі, якщо сила постійна по величині. Побудуємо графік, відкладаючи по осі Х пройдений тілом шлях, а по осі У – проекцію рухомої сили на напрям руху, тобто
В цьому випадку робота миттєвого значення сили на нескінченно малому шляху
А вся робота
Скористаємося (4) для обчислення роботи, яку здійснює сила тяжіння при русі тіла. Розглянемо наприклад, рух тіла масою
Проекція цієї сили на напрям переміщення АВ дорівнює
Величина проекції сили
Звідси слідує, що робота сили тяжіння не залежить від довжини шляху по похилій площині, а залежить тільки від висоти, на яку спустилося тіло, тобто, тільки від початкового та кінцевого положення тіла. Аналогічною властивістю володіє сила пружності. Проаналізуємо більш детально формулу (2): 1) 2) 3) Приклади:
А=0 2. Електричний заряд рухається вздовж еквіпотенціальної поверхні(тобто поверхні з однаковими потенціальними Це також слідує із формули електродинаміки
3. Заряджена частинка рухається в однорідному магнітному полі, на неї діє сила Лоренца, яка за своїм походженням є доцентровою силою.
Отже, сила Лоренца роботи не виконує
4) Приклади:
2. Пружина не навантажена. Сила пружності дорівнює нулю.
Космічні швидкості.
Перша космічна швидкість – це швидкість, яку необхідно надати тілу в горизонтальному напрямку, щоб воно стало штучним супутником Землі. Для того, щоб тіло рухалось поблизу Землі, по кругловій орбіті, тобто стало штучним супутником Землі(ШСЗ) необхідно, щоб доцентрова сила дорівнювала силі тяжіння.
Друга космічна швидкість – це швидкість, яку необхідно надати тілу, для того, щоб воно штучним супутником Сонця. Для цього тілу потрібно надати таку кінетичну енергію, яка дорівнювала б роботі по переміщенню тіла з земної поверхні на нескінченність(практично за межі помітного виміру земного тяжіння). Межі земного тяжіння дорівнюють радіусу Землі.
Третя космічна швидкість – це швидкість необхідна для подолання тіла притягання Сонця. Для цього тілу необхідно надати кінетичну енергію, що дорівнює роботі по переміщенню тіла із земної орбіти на нескінченність. Очевидно, що ця робота дорівнює потенціальній енергії тіла, що знаходиться в полі тяжіння Сонця на відстані земної орбіти від Сонця.
де
Але при цьому треба врахувати, що швидкість Для подолання земного тяжіння, зберігаючи при цьому швидкість
Четверта космічна швидкість. Маючи Астрономічні спостереження показують, що серед зірок, які рухаються навколо центра Галактики на ті й же відстані, що і Сонце, не існує ні однієї зорі, швидкість якої перевищувала б 285 км/с(Саме Сонце має швидкість 220 км/с). Це зумовлено, ймовірно, тим, що швидкість 285 км/с і є та найбільша швидкість при якій зірки можуть залишатись в межах Галактики. При більшій швидкості вони вже не утримуються нашою зірковою системою. Отже четверта космічна швидкість повинна бути дещо більшою 285 км/с, і як показують розрахунки астрофізиків, приблизно дорівнює 290 км/с.
Моменти інерції деяких тіл.
Для неоднорідних тіл і тіл неправильної геометричної форми момент інерції визначають експериментально, а для однорідних тіл геометрично правильної форми – шляхом інтегрування. Завдання. 1. Момент інерції тонкого стержня довжиною 2. Момент інерції бруска довжиною 3. Момент інерції кільця, зовнішній радіус якого 4. Момент інерції тонкостінного кільця(обруча) радіуса 5. Момент інерції диску(циліндру) радіусом 6. Момент інерції кулі радіусом Якщо вісь обертання тіла паралельна осі симетрії
де
Розділ 5. Рівняння руху.
Узагальнені координати.
Для визначення положення системи в Взагалі число незалежних величин, завдання яких необхідне для однозначного визначення положення системи, називається числом її ступенів вільності, в даному випадку це число дорівнює 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.118.36 (0.021 с.) |

 )
)
 , який має свої координати.
, який має свої координати.
 (1),
(1), 1.(2)
1.(2) 1.(3)
1.(3) 1.(4)
1.(4)
 .
.


 .
.
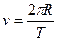 =>
=>  - формула Ейлера.
- формула Ейлера.




 , де
, де  - середнє дотичне(тангенціальне) прискорення,
- середнє дотичне(тангенціальне) прискорення,  - середнє нормальне(доцентрове) прискорення
- середнє нормальне(доцентрове) прискорення






 =>
=>  =>
=> 

 (1)
(1) (2)
(2) ,
,  (3)
(3) (4)
(4)
 Сили, дію яких замінює рівнодійна називають складовими.
Сили, дію яких замінює рівнодійна називають складовими.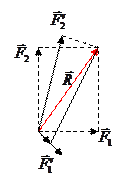
 або
або  і т.п.
і т.п. (5)
(5) - імпульс тіла
- імпульс тіла - зміна імпульсу тіла
- зміна імпульсу тіла - імпульс діючої сили
- імпульс діючої сили
 (6)
(6) - найбільш загальне формулювання ІІ закону Ньютона.
- найбільш загальне формулювання ІІ закону Ньютона.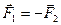
 Третій закон Ньютона не містить ніяких означень і є твердженням, яке вимагає досвідної перевірки.
Третій закон Ньютона не містить ніяких означень і є твердженням, яке вимагає досвідної перевірки.







 - враховуючи додаємо всі:
- враховуючи додаємо всі:
 =>
=> 
 =>
=> 


 - закон збереження імпульсу
- закон збереження імпульсу
 вилітає з гармати зі швидкістю
вилітає з гармати зі швидкістю  при цьому гармата масою
при цьому гармата масою  набуває швидкості -
набуває швидкості -  направленою в протилежну сторону. Тоді
направленою в протилежну сторону. Тоді  =>
=> 
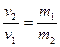
 (1)
(1) (2)
(2) .
. Якщо під час руху величини
Якщо під час руху величини  В границі при нескінченно малих довжинах ділянок шляху робота змінної сили буде чисельно дорівнювати площі фігури на графіку.
В границі при нескінченно малих довжинах ділянок шляху робота змінної сили буде чисельно дорівнювати площі фігури на графіку.
 (3)
(3) (4)
(4) по похилій площині з кутом нахилу
по похилій площині з кутом нахилу  .(мал.3)
.(мал.3) На тіло діє сила тяжіння, під дією якої тіло рухається по похилій площині (тертям нехтуємо).
На тіло діє сила тяжіння, під дією якої тіло рухається по похилій площині (тертям нехтуємо).
 . На переміщення АВ сила
. На переміщення АВ сила 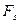 здійснить роботу
здійснить роботу
 де
де  =
=  - висота, на яку спустилося тіло.
- висота, на яку спустилося тіло. ,
, 
 ,
, 
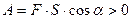
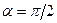 ,
, 

 1. Штучний супутник Землі рухається по кривій орбіті.
1. Штучний супутник Землі рухається по кривій орбіті.
 ), в кожній точці якої вектор сили і вектор переміщення складають кут
), в кожній точці якої вектор сили і вектор переміщення складають кут  , тобто робота не виконується.
, тобто робота не виконується.

 Тобто в кожній точці траєкторії вона складає кут
Тобто в кожній точці траєкторії вона складає кут  з напрямом переміщення.
з напрямом переміщення.



 1.
1.




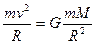 =>
=> 

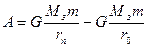



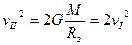
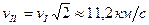
 =>
=> 
 - швидкість тіла відносно Сонця.
- швидкість тіла відносно Сонця. Швидкість
Швидкість 
 , тіло повинно мати після виходу з поля тяжіння Землі. Тому початкова швидкість відльоту тіла з земної поверхні
, тіло повинно мати після виходу з поля тяжіння Землі. Тому початкова швидкість відльоту тіла з земної поверхні  повинна бути дещо більша
повинна бути дещо більша 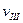 будемо виходити з таких міркувань.
будемо виходити з таких міркувань. , що дорівнює сумі потенціальної енергії на земній поверхні
, що дорівнює сумі потенціальної енергії на земній поверхні  і кінетичної енергії тіла
і кінетичної енергії тіла  . Тоді на основі заходу збереження енергії можемо записати:
. Тоді на основі заходу збереження енергії можемо записати: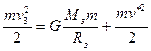
 =>
=> 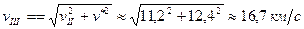
 земне тіло могло б подолати тяжіння Галактики і піти у Всесвіт. Точний розрахунок четвертої космічної швидкості складний. Тому ми обмежимось приблизною оцінкою її величини, виходячи з таких міркувань.
земне тіло могло б подолати тяжіння Галактики і піти у Всесвіт. Точний розрахунок четвертої космічної швидкості складний. Тому ми обмежимось приблизною оцінкою її величини, виходячи з таких міркувань. .
. і шириною
і шириною  .
.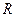 , а внутрішній –
, а внутрішній –  .
.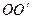 , але зміщена відносно неї на відстань
, але зміщена відносно неї на відстань  , то момент інерції
, то момент інерції  відносно паралельно зміщеної осі виражається співвідношенням, що називається теоремою Штейнера:
відносно паралельно зміщеної осі виражається співвідношенням, що називається теоремою Штейнера: ,
, - момент інерції тіла, відносно осі симетрії.
- момент інерції тіла, відносно осі симетрії.
 матеріальних точок, в просторі треба задати
матеріальних точок, в просторі треба задати 


