
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основний закон обертального руху абсолютно твердого тіла.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Абсолютно тверде тіло визначається як система частинок, зв’язаних між собою такими ньютонівськими силами, які залишають відстані між будь якими двома точками незмінними. Закони поступального руху абсолютно твердих тіл співпадають з першими двома законами руху Ньютона, якщо в них замінити слово „частинка” на „центр мас”.
Нехай тверде тіло довільної форми обертається під дією сили Розкладемо силу Обертальний рух тіла виникає тільки складова
 залежить від моменту сили М. залежить від моменту сили М.
Моментом М обертаючої сили(обертальним моментом) називається добуток сили
Подумки розіб’ємо все тіло на дуже малі частинки – елементарні маси. Хоча сила По ІІ закону Ньютона
де Помноживши обидві частини останньої рівності на радіус
Так як Добуток елементарної маси на квадрат відстані до осі обертання називається моментом інерції матеріальної точки відносно даної осі.
Тоді Просумувавши обертальні моменти
де
Моментом інерції тіла називається сума моментів інерції всіх матеріальних точок, що складають тіло
Формули (4) і (4а) виражають основний закон динаміки обертального руху(ІІ закон Ньютона для обертального руху). Момент обертаючої сили, прикладена до тіла, дорівнює добутку моменту інерції тіла на кутове прискорення. Із формули (4) видно, що кутове прискорення, яке надає тілу обертаючий момент, залежить від моменту інерції тіла: чим більший момент інерції, тим менше кутове прискорення. Отже, момент інерції характеризує інерційні властивості тіл при обертальному русі, подібно тому, як маса характеризує інерційні властивості при поступальному русі. Але, на відміну від маси, момент інерції даного тіла може мати, багато значень у відповідності з множиною можливих осей обертання. Тому, говорячи про момент інерції твердого тіла, необхідно обов’язково вказувати, відносно якої осі він розраховується. Якщо обертальний момент
В наведених формулах
Тому ІІ закон динаміки обертального руху в загальному випадку має такий вигляд:
Швидкість зміни момента імпульса тіла, що обертається, визначається сумарним моментом сил, що діють на тіло. Моменти інерції деяких тіл.
Для неоднорідних тіл і тіл неправильної геометричної форми момент інерції визначають експериментально, а для однорідних тіл геометрично правильної форми – шляхом інтегрування. Завдання. 1. Момент інерції тонкого стержня довжиною 2. Момент інерції бруска довжиною 3. Момент інерції кільця, зовнішній радіус якого 4. Момент інерції тонкостінного кільця(обруча) радіуса 5. Момент інерції диску(циліндру) радіусом 6. Момент інерції кулі радіусом Якщо вісь обертання тіла паралельна осі симетрії
де
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.150 (0.008 с.) |

 Маса тіла і положення його центру мас повністю визначають його поступальний рух. Що стосується обертального руху, то найбільш важливою характеристикою служить тут розподіл речовини відносно центру мас – чи є тіло сильно видовженим, чи навпаки, сплюснутим.
Маса тіла і положення його центру мас повністю визначають його поступальний рух. Що стосується обертального руху, то найбільш важливою характеристикою служить тут розподіл речовини відносно центру мас – чи є тіло сильно видовженим, чи навпаки, сплюснутим. навколо деякої осі
навколо деякої осі 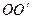 . Тоді всі його точки описують кола з центрами на цій осі, причому всі точки тіла мають однакову кутову швидкість і однакове кутове прискорення в даний момент часу(мал.1).
. Тоді всі його точки описують кола з центрами на цій осі, причому всі точки тіла мають однакову кутову швидкість і однакове кутове прискорення в даний момент часу(мал.1).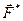 на 3 взаємно перпендикулярні складові
на 3 взаємно перпендикулярні складові  ІІ осі,
ІІ осі,  - дотична.
- дотична. , що описує точка прикладання сили
, що описує точка прикладання сили (1)
(1) . Тоді кожній елементарній масі
. Тоді кожній елементарній масі 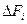 .
. ,
, - лінійне прискорення, яке отримує елементарна маса.
- лінійне прискорення, яке отримує елементарна маса. кола, яке описує елементарна маса і ввівши замість лінійного, кутове прискорення, отримаємо:
кола, яке описує елементарна маса і ввівши замість лінійного, кутове прискорення, отримаємо:

 (2)
(2)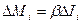
 , прикладені до всіх елементарних мас, що складають тіло, отримаємо:
, прикладені до всіх елементарних мас, що складають тіло, отримаємо: (3)
(3) - обертальний момент, прикладений до тіла.
- обертальний момент, прикладений до тіла. - момент інерції тіла.
- момент інерції тіла. (4)
(4) (4а)
(4а) і момент інерції
і момент інерції  , то формулу (4) можна подати в такому вигляді:
, то формулу (4) можна подати в такому вигляді: або
або  (5)
(5) (5а)
(5а) - проміжок часу, протягом якого кутова швидкість обертання тіла змінюється від
- проміжок часу, протягом якого кутова швидкість обертання тіла змінюється від  до
до  .
. - імпульс моменту сили
- імпульс моменту сили - момент імпульсу
- момент імпульсу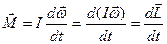
 (6)
(6) .
. і шириною
і шириною  .
.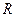 , а внутрішній –
, а внутрішній –  , то момент інерції
, то момент інерції  відносно паралельно зміщеної осі виражається співвідношенням, що називається теоремою Штейнера:
відносно паралельно зміщеної осі виражається співвідношенням, що називається теоремою Штейнера: ,
, - момент інерції тіла, відносно осі симетрії.
- момент інерції тіла, відносно осі симетрії.



