
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Варіаційні задачі на умовний екстремум. Рівняння Ейлера-ЛагранжаСодержание книги
Поиск на нашем сайте
Задачі синтезу алгоритмів оптимального керування об’єктами у динаміці при вибраному функціоналі критерію якості мають додаткові (умовні) обмеження у вигляді рівнянь математичної моделі динаміки об’єкта. Екстремум функціоналу, що визначається за додаткових умов (функціональних обмеженнях), називають умовним екстремумом. Задачі на умовний екстремум при визначенні оптимальних керувань об’єктом у динаміці зумовлені тим, що траєкторія виходу y(t) є наслідком зміни координати керування і залежить від виду диференціального рівняння об’єкта. Таким чином, задача оптимізації об’єкта керування у динаміці, яку розв’язують класичним варіаційним численням, має таке формулювання: - математична модель об’єкта задана у формі рівняння:
- задані граничні умови: y(t0) = y0; y(tк) = yk; - необхідно визначити оптимальне керування u°(t), що забезпечує мінімум функціоналу:
Ця задача називається задачею Лагранжа. Перші задачі на умовний екстремум були поставлені й розв’язані засновниками класичного варіаційного числення Бернуллі, Ейлером і Лагранжем. Розв’язувати задачу на умовний екстремум можна методом множників Лагранжа. Для цього введемо до розгляду новий функціонал:
де l - множник Лагранжа;
За допомогою множників Лагранжа задача про умовний екстремум функціоналу (10.22) приводиться до задачі на безумовний екстремум функціоналу (10.23). Рівняння Ейлера при цьому складають для функції Лагранжа:
Ці рівняння називають рівняннями Ейлера-Лагранжа. Вони характеризують умову стаціонарності функціоналу (10.23). У результаті розв’язування цих рівнянь з урахуванням математичної моделі об’єкта і граничних умов отримаємо оптимальне керування u*(t) об’єктом у динаміці. Приклад 10.2 Визначити оптимальне керування об’єктом, що заданий рівнянням:
у процесі переходу об’єкта з фіксованого початкового стану у фіксований кінцевий стан: y(t0) = y0; y(tк) = yk = 0, за умови мінімуму функціоналу
Запишемо рівняння об’єкта (об’єкт описується аперіодичною ланкою першого порядку) у вигляді:
де а = -1/Т; b = k/T. Складаємо функцію Лагранжа:
Тобто допоміжний функціонал має вигляд:
З урахуванням того, що
записуємо рівняння Ейлера-Лагранжа:
З другого рівняння маємо: u=lb/2, тоді можна записати систему двох рівнянь:
З другого рівняння
або
Розв’язок цього рівняння має вигляд:
де Умовам стійкості та вимогам y(tк) = 0 задовольняє тільки від’ємний корінь, тому маємо:
З урахуванням граничних умов С1=y(o)=y0. Далі знаходимо: Тоді: Шукане оптимальне керування:
де
Рівняння (10.33) визначає структуру оптимального регулятора для заданого об’єкта керування і вибраного функціоналу (10.26). Мінімум цього функціоналу гарантує мінімальні відхилення y(t) і u(t) у період перехідного процесу. Вираз (10.34) визначає оптимальне значення коефіцієнта k0.
Слід нагадати, що при використанні класичного варіаційного числення шукані функції оптимальних процесів є безперервними і на координати виходу та керувань не накладають обмеження. Під час розв’язання задач оптимального керування ці умови далеко не завжди дотримуються. По-перше, керуючі впливи, що входять до функціоналів, можуть бути кусково-безперервними (рис. 10.3). За деяких умов координати об’єкта також мають розрив. Значить, порушуються умови безперервності, що робить розв’язок задачі дуже складним або неможливим.
У першому випадку рівняння Таким чином, порушення умов, на яких ґрунтується класичне варіаційне числення, не дозволяє розв’язувати цими методами широке коло задач теорії автоматичного керування. Ці труднощі можна подолати за допомогою нових методів розв’язування задач теорії оптимальних систем – методу динамічного програмування і принципу максимуму.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.196.68 (0.005 с.) |

 (10.21)
(10.21) (10.22)
(10.22) (10.23)
(10.23) - функція Лагранжа;
- функція Лагранжа; - функція зв’язку.
- функція зв’язку. (10.24)
(10.24) , (10.25)
, (10.25) (10.26)
(10.26)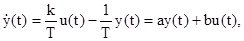
 (10.27)
(10.27) (10.28)
(10.28)
 (10.29)
(10.29) або
або  (10.30)
(10.30) , тоді отримуємо рівняння другого порядку:
, тоді отримуємо рівняння другого порядку:
 (10.31)
(10.31)

 (10.32)
(10.32) ;
; де
де 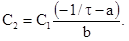
 або з урахуванням (10.32):
або з урахуванням (10.32): (10.33)
(10.33) (10.34)
(10.34)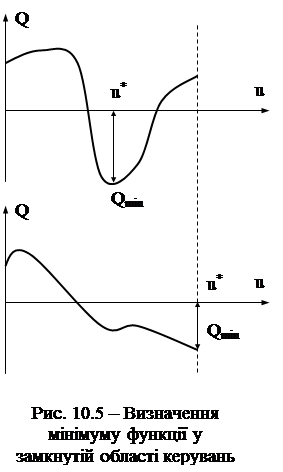 По-друге, у практичних системах на координати і керування завжди накладаються обмеження. Це відповідає тому, що координати і керування можуть змінюватися у деяких замкнутих зонах, а також знаходитись на межах цих зон. Остання обставина може стати причиною серйозних ускладнень. Проілюструємо це за допомогою рис. 10.5.
По-друге, у практичних системах на координати і керування завжди накладаються обмеження. Це відповідає тому, що координати і керування можуть змінюватися у деяких замкнутих зонах, а також знаходитись на межах цих зон. Остання обставина може стати причиною серйозних ускладнень. Проілюструємо це за допомогою рис. 10.5. допомагає знайти оптимальне значення u=u*, при якому Q=Qmin, а у другому маємо мінімум і при невиконанні цієї умови.
допомагає знайти оптимальне значення u=u*, при якому Q=Qmin, а у другому маємо мінімум і при невиконанні цієї умови.


