
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод динамічного програмування БеллманаСодержание книги
Поиск на нашем сайте
У техніці існує клас об’єктів і процесів, керування якими здійснюється на підставі обмеженої кількості рішень, що приймають послідовно у деякі фіксовані моменти часу. Для розв’язування задач оптимізації таких об’єктів американський вчений Р.Беллман запропонував метод, що отримав назву динамічного програмування. Цей термін означає прийняття рішень у часі. За допомогою динамічного програмування можна розв’язувати задачі, що є дискретними за своєю природою. Це має велике значення для найрізноманітніших галузей техніки та економіки, пов’язаних з дискретними процесами виробництва. У основі методу лежить принцип оптимальності. Відповідно до цього принципу оптимальне керування визначається кінцевою метою керування і станом системи у даний момент часу незалежно від того, яким чином система дійшла до цього стану, тобто від “передісторії” системи. Це означає, що для будь-якої оптимальної траєкторії кожна ділянка, яка зв’язує будь-яку проміжну точку цієї траєкторії з кінцевою, також є оптимальною траєкторією. Іншими словами, друга ділянка оптимальної траєкторії є оптимальною траєкторією. Пояснимо метод динамічного програмування на простому прикладі керування об’єктом, рух якого описується рівнянням (10.21):
причому на керуючий вплив накладені обмеження u (t) Необхідно мінімізувати функціонал:
де Для розв’язування задачі Беллман застосував прийом, що полягає у посуванні від кінця процесу (t =T) до його початку (t=0). У результаті було отримане рівняння динамічного програмування у безперервній формі, яке у найпростішому випадку для системи першого порядку з однією керуючою дією має вигляд:
де y0, u0 – початкові значення вихідної координати і керування, S – мінімальне значення функціоналу (10.35), яке залежить від початкових умов. Для отримання мінімуму рівняння (10.36) необхідно продиференціювати за керуванням u. Тоді умову мінімуму (10.36) можна замінити системою:
де y, u – поточні значення вихідної координати і керування. З другого рівняння системи (10.37) визначають dS(y)/dy, а потім з першого рівняння знаходять шукану залежність u=f(y). У випадку, коли система має n вихідних координат і m керувань, рівняння (10.37) матимуть вигляд:
Наведена система рівнянь є найпоширенішою формою запису рівнянь Беллмана. При цьому функція Приклад 10.3 Розв’язати задачу (приклад 10.2) методом динамічного програмування. Маємо рівняння об’єкта: Функціонал: Тоді система (10.37) має вигляд:
Звідси знаходимо: dS/dy = - 2u/b;
Отримали квадратне рівняння відносно u, корені якого є шуканими керуваннями:
Другий корінь відкидаємо як такий, що не відповідає умовам стійкості, й остаточно запишемо:
що співпадає з розв’язком (10.33), (10.34). З рівнянь (10.39) можна виключити u, і тоді визначити функцію S. Приклад 10.4 Розв’язати задачу з обмеженням: де x=f(u) – нелінійна функція з обмеженням (рис. 10.6).
У даному випадку:
Тоді рівняння Беллмана матимуть вигляд:
З другого рівняння отримуємо: Тоді:
Отримали рівняння, аналогічне попередньому прикладу, розв’язок якого має вигляд: Розв’язок рівняння
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.168.68 (0.007 с.) |


 Gu, а також задані початкові умови: y(t0) = y0.
Gu, а також задані початкові умови: y(t0) = y0. (10.35)
(10.35) - деякий функціонал, що залежить від значення вихідної координати у кінці інтервалу часу Т, тобто значення критерію при останньому кроці на ділянці dt (без урахування попередніх).
- деякий функціонал, що залежить від значення вихідної координати у кінці інтервалу часу Т, тобто значення критерію при останньому кроці на ділянці dt (без урахування попередніх). (10.36)
(10.36) (10.37)
(10.37) (10.38)
(10.38) має бути безперервною й диференціюваною за yі, а dS/dyі відіграє ту саму роль, що і множник l у задачі на умовний екстремум. Функція j аналогічна рівнянню зв’язку (10.21).
має бути безперервною й диференціюваною за yі, а dS/dyі відіграє ту саму роль, що і множник l у задачі на умовний екстремум. Функція j аналогічна рівнянню зв’язку (10.21).

 (10.39)
(10.39) або
або 



 Функціонал, що мінімізується, має вигляд:
Функціонал, що мінімізується, має вигляд:

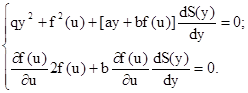 (10.40)
(10.40)
 ;
;
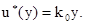
 дає константу f(u)=const. З урахуванням обмежень маємо |f(u)| = C.
дає константу f(u)=const. З урахуванням обмежень маємо |f(u)| = C.


