
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Варіаційна задача з закріпленими граничними точками. Рівняння ЕйлераСодержание книги
Поиск на нашем сайте
де y = y(t), Технічна задача оптимізації динаміки об’єкта приводиться до математичної задачі знаходження екстремуму функціоналу (10.13). При цьому шукана функція повинна задовольняти крайовим умовам: y(t0) = y0; y(tк) = yk, де y0, yk – задані числа. Така задача називається варіаційною задачею із закріпленими граничними точками (із закріпленими кінцями) (рис. 10.4). Умова екстремуму інтегралу (10.13) при фіксованих граничних значеннях і відсутності обмежень на координати записується у вигляді рівняння Ейлера:
Криві, на яких реалізується екстремум функціоналу (екстремалі), є інтегральними кривими цього рівняння. Для з’ясування, чи відповідає знайдена екстремаль мінімуму функціоналу, необхідно перевірити виконання додаткових умов. Оскільки це є достатньо складною процедурою, на практиці іноді обмежуються чисельною перевіркою значення функціоналу біля знайденої екстремалі. Приклад 10.1 Знайти криву y*(t), що проходить у фіксовані моменти часу t0 і tk через задані точки у0 і уk, на якій досягає екстремуму функціонал:
де k – задане число (k>0). У даному випадку Рівняння Ейлера для екстремалей функціоналу (10.15) має вигляд:
Розв’язок цього рівняння запишемо у вигляді:
Для визначення С1 і С2 використовуємо граничні умови:
Тоді отримуємо:
У задачах оптимізації динаміки об’єктів у загальному випадку функціонал (10.13) може містити похідні вищих порядків. Необхідну умову наявності екстремуму такого функціоналу визначає рівняння Ейлера-Пуассона (за фіксованих граничних умов і відсутності обмежень на координати):
Слід зазначити, що рівняння (10.14) і (10.19) застосовуються для знаходження екстремумів відповідних функціоналів тільки тоді, коли координати y(t) є безперервними гладкими функціями і не мають обмежень типу нерівностей. Ці рівняння виражають першу необхідну умову екстремуму. Однак, залишається неясним, є отримані екстремалі максимумом чи мінімумом функціоналу. Відповідь на це запитання дає теорема Лежандра, яка виражає другу необхідну умову екстремуму:
Для того, щоб функціонал (10.13) у задачі із закріпленими кінцями досягав на кривій мінімуму (максимуму), необхідно, щоб уздовж цієї кривої виконувалась умова:
Так, для прикладу (10.1) маємо:
значить, на кривій (10.17) функціонал (10.15) досягає мінімуму.
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.84.179 (0.006 с.) |

 Під час вивчення перехідних процесів систем керування характер динаміки можна оцінювати величиною визначеного інтегралу. Наприклад, для одномірних об’єктів:
Під час вивчення перехідних процесів систем керування характер динаміки можна оцінювати величиною визначеного інтегралу. Наприклад, для одномірних об’єктів: (10.13)
(10.13) - траєкторії координати виходу та її першої похідної за часом.
- траєкторії координати виходу та її першої похідної за часом. (10.14)
(10.14) (10.15)
(10.15)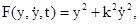 тому
тому 
 або
або  (10.16)
(10.16) . (10.17)
. (10.17)
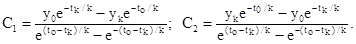 (10.18)
(10.18) (10.19)
(10.19) (10.20)
(10.20)



