
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обмеження фазових координат і керуваньСодержание книги
Поиск на нашем сайте
Об’єкт керування можна подати у вигляді, що наведений на рис. 10.1. Величини u1(t), …, um(t) зручно вважати координатами деякого вектора u = (u1, u2, …um) у m-мірному просторі керування. Вектор u називають вектором керування або керуванням. Величини y1(t), …, yn(t) розглядають як координати вектора y = (y1, …, yn) у n-мірному просторі, який називають фазовим простором об’єкта, що розглядають. Вектор y називають фазовим вектором або вектором стану. Він визначає стан об’єкта у даний момент часу. Якщо стан об’єкта характеризується двома фазовими координатами, то кажуть про фазову площину. Розмірність векторів u і y може бути однаковою або відрізнятися одна від одної (m£n). Пару векторних функцій [ u (t), y (t)] називають процесом керування або просто процесом. Під час розробки оптимальних систем автоматичного керування необхідно враховувати різні обмеження, що накладають на координати і показники якості процесу. Усі обмеження координат і керувань можна розділити на два типи: природні та умовні. Природні обмеження фазових координат обумовлені принципом роботи об’єкта. Наприклад, частота обертання асинхронного електродвигуна не може бути більшою за синхронну частоту; вихідні сигнали підсилювача обмежені через явище насичення і т.д. Умовні обмеження координат уводять свідомо. Наприклад, величину струму якоря електродвигуна постійного струму обмежують умовами нормальної комутації на колекторі, нагрівом струмопровідних частин, граничною температурою ізоляції обмоток. Наявність умовних обмежень координат звичайно обумовлює введення обмежень на керування. Іншими словами, вектори u (t) і y (t) можуть змінюватись лише у деякій зоні, що допускається: u (t)
У загальному випадку область керування може мати геометрично більш складний характер, оскільки через конструкцію об’єкта між керуючими параметрами ui можуть існувати зв’язки, що виражаються рівняннями вигляду:
Для технічних систем особливо важливим і характерним є випадок замкнутої множини Gu, тобто випадок, коли точка може знаходитись не тільки всередині цієї множини, а і на її межі.
Функція u(t) при t0 £ t £ t1 називається кусково-безперервною, якщо складається зі скінченної кількості безперервних кусків, тобто є безперервною для всіх моментів часу t, за винятком лише скінченної кількості цих моментів, де функція u(t) може мати розрив першого роду (рис. 10.3). Кусково-безперервні керування дозволяють отримати для достатньо широкого класу прикладів точний математичний розв’язок оптимальної задачі та є достатньо наочними і зручними для технічної реалізації. Критерії оптимальності Важним етапом під час розробки оптимальних систем є формулювання мети оптимізації, яка математично виражається як вимога забезпечення мінімуму чи максимуму деякого показника якості (критерію оптимальності). Як критерій оптимальності, можуть бути прийняті різні технічні та техніко-економічні показники й оцінки. Наприклад, критерій може відображати техніко-економічну вигоду (продуктивність, коефіцієнт корисної дії тощо), при цьому оптимальне керування повинне забезпечувати максимум критерію оптимальності; він може виражати також утрати (витрату енергії, палива, коштів і т.д.), у цьому випадку оптимальне керування забезпечує мінімум критерію. Цільову функцію необхідно подати у формі, яка допускає використання будь-якого відомого методу синтезу оптимальних систем. Під час розробки найпростіших локальних систем керування звичайно розглядають задачу оптимізації за критеріями, що характеризують якість функціонування системи (точність, швидкодію), а інші критерії не враховують. У теорії автоматичного керування широко розповсюджені функціонали, що характеризують якість системи. Змінна величина I[x(t)] називається функціоналом, що залежить від функції x(t), якщо кожній функції x(t) відповідає число I. У загальному випадку функціонал залежить від фазових координат yi(t), координат керування uj(t), збурюючих впливів zk(t) і може бути поданий у вигляді:
де [t0, t1] – інтервал часу, що розглядають; F – визначена функція, яка відображає показник якості; y, u, z – вектори фазових змінних, керувань і збурень відповідно. Досягнення максимального чи мінімального (екстремального) значення цього функціоналу вказує на оптимальну роботу чи стан системи. Розглянемо деякі типи критеріїв оптимальності найпростіших об’єктів і систем керування складними процесами. Час перехідного процесу:
Отримана при цьому система є оптимальною за швидкодією, якщо вона забезпечує мінімум інтегралу (10.4) з урахуванням обмежень координат. Інтегральні оцінки якості перехідного процесу:
де e(t) = y*(t)–y(t) – відхилення вихідної змінної y(t) від заданого значення y*(t);
За умови забезпечення мінімуму інтегралу (10.5) система є оптимальною за точністю у динамічних режимах при ступінчастому задавальному впливі. За умови забезпечення мінімуму функціоналів (10.6) і (10.7) система є оптимальною за точністю у статичному розумінні. Для визначення коливальності перехідного процесу, тобто характеру його протікання, застосовують узагальнений інтегральний квадратичний критерій:
де rі – вагові коефіцієнти. Перший доданок у виразі (10.8) забороняє тривале існування відхилення вихідної координати у, а подальші доданки – тривале існування великих значень похідних. Тому мінімуму інтегралу (10.8) відповідають достатньо швидкоплинні й плавні перехідні процеси. Зазначимо, що інтегральні критерії (10.5) – (10.8) не враховують того, що у системі можуть мати місце обмеження потужності сигналу керування. Крім того, система сама може мати обмежені енергетичні ресурси. Ці обмеження враховують функціонали вигляду:
Перший доданок у виразі (10.9) має той самий смисл, що й у виразі (10.8). Другий доданок, з одного боку, означає досягнення оптимальності гасіння збуреного руху за умови обмеження витрат енергії на керування, а з іншого – забезпечує пошук оптимального керування серед множини лінійних функцій, що допускаються. Витрати енергії на керування:
де u(t) та i(t) – напруга і струм навантаження; r=1/R – коефіцієнт пропорційності; R – опір електричного ланцюга. Даний критерій також використовують при керуванні від джерел енергії, що є обмеженими за потужністю. У механічних системах для оцінювання енергії керування іноді беруть функціонал вигляду:
де u(t) – координата керування; Витрати палива:
За умови мінімуму цього інтегралу отримуємо систему, оптимальну за витратами палива. У випадках, коли необхідно забезпечити найкращу роботу системи за найгірших можливих умов, застосовують мінімаксний критерій оптимальності. Формування критерію оптимальності, що визначає мету оптимізації, - це інженерна та інженерно-економічна задача, яку розв’язують на підставі глибокого та всебічного вивчення об’єкта, яким керують. Якщо необхідно врахувати різні показники якості, задача вибору критерію оптимальності ускладнюється, оскільки вимоги до системи звичайно є суперечними. У зв’язку з цим як основний беруть критерій якості функціонування.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.175 (0.006 с.) |

 Gu; y (t)
Gu; y (t)  Першу умову називають обмеженням на керування, другу – фазовим обмеженням. Gu і Gy – деякі задані множини. Множину Gu називають областю керування. Її вказують у математичному описі об’єкта. Наприклад, якщо параметри u1 і u2 характеризують на площині векторну величину, модуль якої не перевищує одиниці, а напрямок довільний, то ці параметри підкоряються умові
Першу умову називають обмеженням на керування, другу – фазовим обмеженням. Gu і Gy – деякі задані множини. Множину Gu називають областю керування. Її вказують у математичному описі об’єкта. Наприклад, якщо параметри u1 і u2 характеризують на площині векторну величину, модуль якої не перевищує одиниці, а напрямок довільний, то ці параметри підкоряються умові  , а область керування Gu являє собою круг одиничного радіусу (рис. 10.2).
, а область керування Gu являє собою круг одиничного радіусу (рис. 10.2).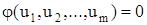 . (10.2)
. (10.2) Важливо зробити ще одне припущення: значення керуючих параметрів можуть змінюватися стрибком, тобто ці параметри є безінерційними. Тому необхідно розглядати не тільки безперервні, а й кусково-безперервні керування.
Важливо зробити ще одне припущення: значення керуючих параметрів можуть змінюватися стрибком, тобто ці параметри є безінерційними. Тому необхідно розглядати не тільки безперервні, а й кусково-безперервні керування. y, u, z ]dt, (10.3)
y, u, z ]dt, (10.3) (10.4)
(10.4) (10.5)
(10.5) (10.6)
(10.6) (10.7)
(10.7) - середнє значення квадрату помилки системи;
- середнє значення квадрату помилки системи; - середнє значення квадрату вихідної координати.
- середнє значення квадрату вихідної координати. (10.8)
(10.8) (10.9)
(10.9) (10.10)
(10.10) (10.11)
(10.11) - похідна вихідної змінної об’єкта.
- похідна вихідної змінної об’єкта. . (10.12)
. (10.12)


