
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення границі функції і її властивості.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо приклади, що розкривають зміст поняття границі функції. Приклад 3.1. Розглянемо функцію Приклад 3.2. Розглянемо функцію Означення 1 (за Гейне). Нехай функція Символічний запис: Як приклад, Для доведення деяких властивостей функцій, що мають границю, використовують означення границі функції за Коші: Означення 2. Число Можна довести, що означення границі функції за Коші і Гейне рівносильні. Означення. Число Позначення: Ліва і права границі називаються односторонніми границями. Очевидно, для того щоб функція
Властивості функцій, що мають границю. Теорема 1. (про обмеженість). Якщо функція Теорема 2. (про збереження знаку). Якщо функція Зауважимо, що обидві теореми носять локальний характер, тобто виконуються для точок, що лежать поблизу точки Також слід зауважити, що для границі функції справедливі арифметичні теореми і теореми порівняння, аналогічні відповідним теоремам про границю послідовності.
Розкриття невизначеностей. При знаходженні границь функцій (послідовностей) ми користуємось арифметичними теоремами в припущенні, що відповідні границі існують, а для частки з додатковою умовою, що границя знаменника відміна від нуля. В деяких випадках, що залишились без розгляду (коли границі функцій (одна або обидві) нескінченні чи не існують, або у випадку частки - границя знаменника дорівнює нулю) можна цілком визначено сказати як поводить себе відповідна функція. Наприклад, якщо Проте, якщо а) невизначеність Якщо 1) 2)
В другому прикладі для виділення множника б) невизначеність Нехай 1) 2) 3) Наведені приклади можна об'єднати в загальне правило: границя відношення двох многочленів дорівнює
де в) невизначеність Нехай Приклад 3.3 Знайти Розв’язування.
г) невизначеність Розглянемо Завдання для самостійного розв’язування. 3.1 Знайти границі: а) в) д) 3.2 Знайти границі: а) в) д). 3.3 Знайти границі: а) в) д) є) 3.4 Знайти границі: а) в) д) Відповіді: 3.1 а) 3.2 а) 0; б) 3.3 а) є) 3.4 а)
Чудові границі. 1) В попередньому параграфі було встановлено, що Поклавши
Приклад 3.4 Знайти: а) Розв’язування. а) б)
2) Другою чудовою границею називається
В усіх цих співвідношеннях розглядається відношення двох нескінченно малих величин при умові, що Приклад 3.5 Знайти а) Розв’язування. а) б) Завдання для самостійного розв’язування. 3.5 Знайти границі: а) в) д) є) 3.6 Знайти границі: а) в) д). є) Відповіді: 3.5 а) є) 3.6 а) є) 8; ж) 1.
§ 4. Неперервність функції. З поняттям границі функції тісно пов’язано і інше важливе поняття математичного аналізу – поняття неперервності функції. Інтуїтивно поняття неперервності функції пов’язано з графіком функції: функція вважається неперервною, якщо її графік можна провести лінією, не відриваючи олівця від паперу. Що ж станеться, якщо зробити в якійсь точці "прокол"? Тоді перпендикуляр, проведений з цієї точки на ось абсцис, не перетне графіка функції, що рівносильно відсутності значення функції в цій точці. Отже перший висновок: неперервна функція повинна мати значення в точці Означення 1. Функція 1. функція визначена в околі точки 2. функція має границю в точці 3. ця границя дорівнює значенню функції в точці Приклад 4.1 Дослідити неперервність в точці а) Розв’язування. а) В точці б) В точці в) В точці Означення неперервності функції в точці Поняття неперервності можна сформулювати і на мові приростів. Приростом аргументу Означення 2 Функція
Приклад 4.2 Довести неперервність функції Розв’язування. Розглянемо довільну точку Для функцій, неперервних в точці Теорема 1. Якщо функції
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.3 (0.008 с.) |

 в деякому околі точки
в деякому околі точки  . З цього околу виберемо довільну послідовність аргументу
. З цього околу виберемо довільну послідовність аргументу  , наприклад
, наприклад  . Обчисливши значення функції
. Обчисливши значення функції  для кожного члена послідовності, одержимо послідовність відповідних значень
для кожного члена послідовності, одержимо послідовність відповідних значень  . Очевидно
. Очевидно  . Виберемо іншу послідовність значень аргументу
. Виберемо іншу послідовність значень аргументу  з того ж самого околу, наприклад,
з того ж самого околу, наприклад,  . Складена для неї послідовність відповідних значень заданої функції має вигляд:
. Складена для неї послідовність відповідних значень заданої функції має вигляд:  . Очевидно
. Очевидно  . Отже, для довільних послідовностей аргументу
. Отже, для довільних послідовностей аргументу  відповідних значень заданої функції
відповідних значень заданої функції 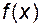 має одну і ту ж границю 1.
має одну і ту ж границю 1. в околі радіуса 1 якої-небудь цілої точки, наприклад,
в околі радіуса 1 якої-небудь цілої точки, наприклад,  для будь-якого
для будь-якого  . Складемо для неї послідовність відповідних значень заданої функції. Одержимо послідовність
. Складемо для неї послідовність відповідних значень заданої функції. Одержимо послідовність  , яка має границю 0. Виберемо тепер в правому півоколі довільну послідовність
, яка має границю 0. Виберемо тепер в правому півоколі довільну послідовність  для будь-якого
для будь-якого  , яка має границю 1. Таким чином, на відміну від попереднього прикладу для різних послідовностей аргументу, що мають границю 1, послідовності відповідних значень функції
, яка має границю 1. Таким чином, на відміну від попереднього прикладу для різних послідовностей аргументу, що мають границю 1, послідовності відповідних значень функції  ,
,  мають різні границі.
мають різні границі.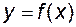 визначена в деякому околі точки
визначена в деякому околі точки  , за винятком, можливо, самої точки
, за винятком, можливо, самої точки  називається границею функції
називається границею функції  (або в точці
(або в точці  і такої, що
і такої, що  , відповідна послідовність
, відповідна послідовність  .
.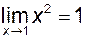 , а функція
, а функція  не має границі в точці
не має границі в точці  існує число
існує число  таке, що з нерівностей
таке, що з нерівностей  випливає нерівність
випливає нерівність  .
. називається лівою (правою) границею функції
називається лівою (правою) границею функції  , відповідна послідовність
, відповідна послідовність  ,
,  .
. вона обмежена.
вона обмежена. при
при  ,
,  ,
,  , то
, то  ,
,  ,
, 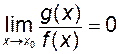 ,
,  .
. , то про границю частки
, то про границю частки  ніякого загального твердження ми зробити не можемо. Наприклад, нехай
ніякого загального твердження ми зробити не можемо. Наприклад, нехай  ,
,  . Обидві функції при
. Обидві функції при  прямують до нуля. Їх відношення
прямують до нуля. Їх відношення  також прямує до нуля, коли
також прямує до нуля, коли  . Якщо ж, навпаки,
. Якщо ж, навпаки,  ,
,  , то
, то 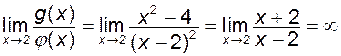 . Отже, в залежності від вигляду обох функцій, границя частки може існувати, а може і не існувати. В зв’язку з цим говорять, що мають справу з невизначеністю. А задача знаходження границі в кожному такому випадку називається задачею розкриття невизначеності. Розглянемо найбільш важливі випадки:
. Отже, в залежності від вигляду обох функцій, границя частки може існувати, а може і не існувати. В зв’язку з цим говорять, що мають справу з невизначеністю. А задача знаходження границі в кожному такому випадку називається задачею розкриття невизначеності. Розглянемо найбільш важливі випадки: .
. і
і  ми маємо невизначеність
ми маємо невизначеність  є алгебраїчними, то для розкриття невизначеності в чисельнику і знаменнику слід виділити множник
є алгебраїчними, то для розкриття невизначеності в чисельнику і знаменнику слід виділити множник  , щоб в подальшому скоротити дріб на цей множник:
, щоб в подальшому скоротити дріб на цей множник: .
.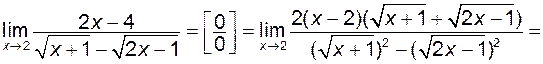
 .
. знищили ірраціональність в знаменнику шляхом домноження на спряжений вираз.
знищили ірраціональність в знаменнику шляхом домноження на спряжений вираз. .
. ,
,  при
при  . В цьому випадку вираз
. В цьому випадку вираз  ,
,  ,
,  - ціле невід'ємне число, називається многочленом. Перший доданок
- ціле невід'ємне число, називається многочленом. Перший доданок  називається старшим членом,
називається старшим членом,  визначається поведінкою старшого члена, тобто
визначається поведінкою старшого члена, тобто  . Тому:
. Тому: ,
, ,
, .
. , якщо степінь чисельника більший степеня знаменника; дорівнює 0, якщо степінь чисельника менший степеня знаменника, і дорівнює відношенню коефіцієнтів при старших членах, якщо степені чисельника і знаменника рівні, тобто
, якщо степінь чисельника більший степеня знаменника; дорівнює 0, якщо степінь чисельника менший степеня знаменника, і дорівнює відношенню коефіцієнтів при старших членах, якщо степені чисельника і знаменника рівні, тобто ,
, степені многочленів
степені многочленів  відповідно.
відповідно. .
. . Тоді вираз
. Тоді вираз  дає невизначеність
дає невизначеність  .
.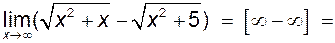
 .
. .
. . Якщо
. Якщо  при
при  , то вираз
, то вираз  ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  ;
; ; ж)
; ж)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  .
. б)
б)  в)
в)  г)
г)  д) 0; е) 6;
д) 0; е) 6; ; г)
; г)  д)
д)  е)
е) 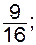
 ; б)
; б)  в)
в)  г)
г)  д)
д)  е) -5;
е) -5; б)
б)  . Розглянемо функцію
. Розглянемо функцію  . Ця функція існує для всіх
. Ця функція існує для всіх  крім
крім  . Можна довести, що
. Можна довести, що  . Слід звернути увагу на те, що основа степеня
. Слід звернути увагу на те, що основа степеня  при
при  , а показник степеня
, а показник степеня  дає невизначеність
дає невизначеність  .
. , знайдемо
, знайдемо  . При
. При  . У результаті отримаємо ще один запис числа
. У результаті отримаємо ще один запис числа  :
:  . Обидва розглянутих співвідношення носять назву першої чудової границі і можуть бути використані для розкриття невизначеності
. Обидва розглянутих співвідношення носять назву першої чудової границі і можуть бути використані для розкриття невизначеності 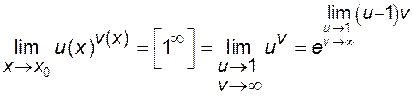
 ; б)
; б)  .
. .
.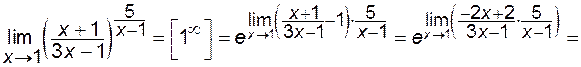
 .
. . Скориставшись даним співвідношенням, можна довести, що
. Скориставшись даним співвідношенням, можна довести, що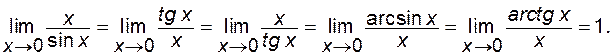
 . Отже всі вони можуть бути використані для розкриття невизначеностей
. Отже всі вони можуть бути використані для розкриття невизначеностей  ; б)
; б)  .
. .
. .
. ; б)
; б) 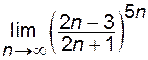 ;
; ; г)
; г)  ;
;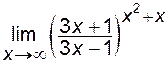 ; е)
; е)  ;
; ; ж)
; ж)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  ;
; . ж)
. ж)  .
. ; б)
; б)  ; в) 1; г)
; в) 1; г)  ;
; ; ж) e.
; ж) e. ; б)
; б)  ; в) 2; г)
; в) 2; г)  ; д)
; д)  ; е) 8;
; е) 8; ;
; ;
; .
. функцій:
функцій: ; в)
; в)  .
. (точніше, тут існують односторонні границі функції: лівостороння
(точніше, тут існують односторонні границі функції: лівостороння  і правостороння
і правостороння  , проте їх значення не співпадають).
, проте їх значення не співпадають). .
. , тобто для неперервної функції можливе переставлення символів границі і функції.
, тобто для неперервної функції можливе переставлення символів границі і функції. в точці
в точці  . Звідки
. Звідки  . Приростом функції
. Приростом функції  .
. .
. .
. і задамо приріст
і задамо приріст  . Тоді
. Тоді  . Знайдемо
. Знайдемо  . Отже за другим означенням неперервності функція
. Отже за другим означенням неперервності функція  неперервні в точці
неперервні в точці  ,
,  ,
,  .(остання – при додатковій умові, що
.(остання – при додатковій умові, що  ).
).


