
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класифікація та деякі властивості функцій.Содержание книги
Поиск на нашем сайте В багатьох випадках знання особливостей функцій допомагає побудувати їх графіки. Розглянемо деякі типи функцій. Означення. Функція Протилежне поняття формулюється так: Означення. Функція Графік обмеженої функції розміщується між двома прямими, паралельними осі Означення. Функція
Рис.1. Означення. Функція Графік парної функції симетричний відносно осі
Рис.2 Рис.3
Обернена функція. Нехай функція Якщо кожному значенню Зауваження. Означення оберненої функції може бути узагальнено і для випадків коли Приклад. Функція Проте не всяка функція Теорема. Якщо функція Функція Легко помітити, що
Елементарні функції. Означення. Основні елементарні функції: степенева З основними елементарними функціями ми познайомились в шкільному курсі математики, а тому їх властивості пропонуємо розглянути самостійно.
§ 2. Послідовність. Границя послідовності.
Функція, задана на множині натуральних чисел, називається числовою послідовністю. Позначається Наприклад, нехай задано загальний член послідовності Приклад 2.1. Побудувати числову послідовність для знаходження грошових накопичень з урахуванням складних процентів. Розв'язок. Нехай початкова сума вкладу складає На кінець першого року сума вкладу складе
Розглянемо послідовності
З рисунку видно, що члени послідовності Виберемо Означення 1. Число Якщо члени послідовності належать Означення 2. Число
Границя числової послідовності позначається Приклад 2.2 Довести, що для послідовності Розв'язування. Для будь-якого Приклад 2.3 Довести, що послідовність Розв’язування. При будь-якому Послідовності, які мають границю, називаються збіжними, а ті що не мають – розбіжними.
Обмежені послідовності. Зв'язок між існуванням границі та її обмеженістю. Означення. Послідовність Теорема. Якщо послідовність Доведення. Нехай Зауважимо, що протилежне твердження в цілому не вірне. Наприклад, послідовність
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.158 (0.008 с.) |

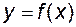 , визначена на множині
, визначена на множині  , називається обмеженою на цій множині, якщо існує
, називається обмеженою на цій множині, якщо існує  таке число
таке число  , що для всіх
, що для всіх 
 виконується нерівність
виконується нерівність  .
. , існує
, існує 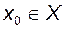 таке, що виконується нерівність
таке, що виконується нерівність  .
. :
:  та
та  .
. , називається зростаючою (неспадною, спадною, незростаючою) на цьому проміжку, якщо для всіх
, називається зростаючою (неспадною, спадною, незростаючою) на цьому проміжку, якщо для всіх  і
і  з цього проміжку, що задовольняють нерівності
з цього проміжку, що задовольняють нерівності  виконується нерівність
виконується нерівність  (
( ,
,  ,
,  ).
).
 , розміщеній симетрично відносно початку координат, називається парною (непарною), якщо для
, розміщеній симетрично відносно початку координат, називається парною (непарною), якщо для  виконується рівність
виконується рівність  (
( ).
). (Рис.2), а графік непарної функції – симетричний відносно початку координат (Рис.3). Ця особливість графіків парної та непарної функцій дає змогу скоротити роботу з побудовою графіків таких функцій: досить побудувати графік функції тільки в правій півплощині.
(Рис.2), а графік непарної функції – симетричний відносно початку координат (Рис.3). Ця особливість графіків парної та непарної функцій дає змогу скоротити роботу з побудовою графіків таких функцій: досить побудувати графік функції тільки в правій півплощині.

 , а множиною її значень є відрізок
, а множиною її значень є відрізок 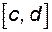 , тобто
, тобто  ,
,  .
. відповідає єдине значення
відповідає єдине значення  , для якого
, для якого  , то на відрізку
, то на відрізку  , яка називається оберненою по відношенню до функції
, яка називається оберненою по відношенню до функції 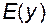 є будь-які проміжки, а не тільки відрізки.
є будь-які проміжки, а не тільки відрізки. визначена на
визначена на 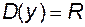 . Оберненою для неї є функція
. Оберненою для неї є функція  , що також визначена на
, що також визначена на 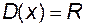 .
. , оберненої не має, оскільки двом різним точкам
, оберненої не має, оскільки двом різним точкам  і
і 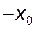 вона ставить у відповідність одну точку
вона ставить у відповідність одну точку  . Сформулюємо теорему існування оберненої функції:
. Сформулюємо теорему існування оберненої функції: , має обернену
, має обернену  , оскільки кожним двом різним точкам
, оскільки кожним двом різним точкам  , вона ставить у відповідність дві різні точки
, вона ставить у відповідність дві різні точки  .
. , а функція
, а функція  .
. , показникова
, показникова 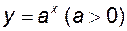 , обернена до степеневої
, обернена до степеневої  , логарифмічна
, логарифмічна  , тригонометричні
, тригонометричні 


 обернені тригонометричні
обернені тригонометричні 


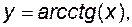 а також функції, знайдені за допомогою формул, що містять скінчене число арифметичних дій (додавання, віднімання, множення, ділення) і суперпозицій основних елементарних функцій, називаються елементарними функціями.
а також функції, знайдені за допомогою формул, що містять скінчене число арифметичних дій (додавання, віднімання, множення, ділення) і суперпозицій основних елементарних функцій, називаються елементарними функціями. де
де  – загальний член послідовності. Кожна числова послідовність вважається заданою, якщо вказано правило чи закон її утворення.
– загальний член послідовності. Кожна числова послідовність вважається заданою, якщо вказано правило чи закон її утворення.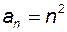 , тоді її членами будуть числа
, тоді її членами будуть числа  . Для послідовностей з загальними членами
. Для послідовностей з загальними членами 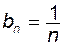 ,
,  членами будуть відповідно числа:
членами будуть відповідно числа:  та
та 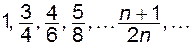
 грн., процентна ставка дорівнює
грн., процентна ставка дорівнює  річних. Величина
річних. Величина  називається питомою процентною ставкою.
називається питомою процентною ставкою. , на кінець другого року –
, на кінець другого року –  , на кінець
, на кінець  року –
року –  .
. і
і  . Побудуємо точки на числовій осі, що відповідають членам цих послідовностей:
. Побудуємо точки на числовій осі, що відповідають членам цих послідовностей: наближаються до точки 0, члени другої послідовності необмежено віддаляються від початку координат.
наближаються до точки 0, члени другої послідовності необмежено віддаляються від початку координат. - окіл точки 0 з
- окіл точки 0 з  . Поза цим околом знаходяться десять перших членів, всі інші, тобто всі починаючи з номера
. Поза цим околом знаходяться десять перших членів, всі інші, тобто всі починаючи з номера  , належать цьому околу. Виберемо менший окіл точки 0, наприклад
, належать цьому околу. Виберемо менший окіл точки 0, наприклад  . Поза цим околом знаходяться перші сто членів, а всі інші, починаючи з номера
. Поза цим околом знаходяться перші сто членів, а всі інші, починаючи з номера  , належать вибраному околу.
, належать вибраному околу.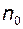 , а поза ним знаходиться фіксоване число членів послідовності.
, а поза ним знаходиться фіксоване число членів послідовності. , або згідно властивості 7 модуля
, або згідно властивості 7 модуля  .
. існує такий номер
існує такий номер  виконується нерівність
виконується нерівність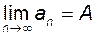 або
або  .
.
 .
.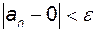 або
або  виконується при
виконується при  . Отже, при будь-якому
. Отже, при будь-якому 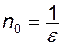 (або рівний цілій частині
(або рівний цілій частині 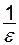 ), що для всіх
), що для всіх  . А це означає, що
. А це означає, що  .
. не має границі.
не має границі. на числовій осі не має жодної точки
на числовій осі не має жодної точки  виконується нерівність
виконується нерівність 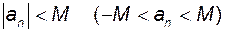 .
. існує номер такий номер
існує номер такий номер  . Тоді для всіх
. Тоді для всіх  , а отже послідовність
, а отже послідовність 


