Розділ іII. Вступ до аналізу.
Розділ ІII. Вступ до аналізу.
§ 1. Означення функції. Основні поняття та властивості функцій. Графік функції.
Дійсні числа. Модуль числа та його властивості.
Дійсним числом називається будь-який десятковий дріб, скінчений чи нескінчений. Якщо  – деяка множина дійсних чисел, то запис – деяка множина дійсних чисел, то запис  означає, що число означає, що число  належить належить  . Відомо, що кожному дійсному числу на числовій осі відповідає єдина точка. . Відомо, що кожному дійсному числу на числовій осі відповідає єдина точка.
Множина дійсних чисел  (або точок на числовій осі), що задовольняють нерівності (або точок на числовій осі), що задовольняють нерівності 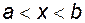 ( ( ), де ), де  – фіксовані числа, називається інтервалом (відрізком) і позначається – фіксовані числа, називається інтервалом (відрізком) і позначається  ( ( ). ).
Множина дійсних чисел  , що задовольняють нерівності , що задовольняють нерівності  або або  , називається півінтервалом. , називається півінтервалом.
Надалі, у випадках коли належність чи неналежність множині граничних точок  немає суттєвого значення, інтервал, відрізок, півінтервал будемо називати проміжком і позначати немає суттєвого значення, інтервал, відрізок, півінтервал будемо називати проміжком і позначати  . .
Інтервал  , ,  називається називається  – околом точки – околом точки  . .
Для позначення відстані довільної точки  числової осі до початку координат використовують числової осі до початку координат використовують  – модуль числа. – модуль числа.
Означення. Модулем числа  називається називається
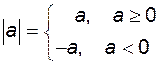
Наприклад:  . .
Властивості модуля:
1.  2. 2. 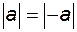
3.  4. 4. 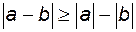
5. 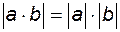 6. 6. 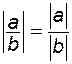
7. Нерівність  означає, що означає, що 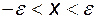 . .
Означення та способи задання функції. Графік функції.
Нехай задано множину чисел  . Говорять, що на множині . Говорять, що на множині  задано функцію задано функцію  , якщо кожному , якщо кожному  відповідає одне певне число відповідає одне певне число  і записують і записують 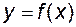 . При цьому . При цьому  називають незалежною зміною або аргументом, а називають незалежною зміною або аргументом, а  – залежною зміною або функцією. – залежною зміною або функцією.
Множина  називається областю визначення функції і позначається називається областю визначення функції і позначається  або або  , ,  – значення функції в точці – значення функції в точці  , а сукупність , а сукупність  всіх таких значень – областю значень функції і позначається всіх таких значень – областю значень функції і позначається  або або 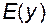 . .
З означення функції випливає, що функція вважається заданою, якщо вказано закон відповідності і область визначення. Якщо область визначення функції 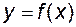 складається з усіх складається з усіх  , для яких вираз , для яких вираз 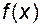 має значення, то таку область визначення будемо називати максимальною областю визначення або областю існування. В подальших прикладах знаходження області визначення функції пов’язане тільки із знаходженням області існування. має значення, то таку область визначення будемо називати максимальною областю визначення або областю існування. В подальших прикладах знаходження області визначення функції пов’язане тільки із знаходженням області існування.
Приклад 1.1. Знайти область визначення функції  . .
Розв’язування. Очевидно, що вираз  має сенс тоді і тільки тоді, коли має сенс тоді і тільки тоді, коли  , або , або 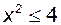 . Так як . Так як  , то , то  . Згідно властивості 7 модуля . Згідно властивості 7 модуля  . Отже, область визначення функції є відрізок . Отже, область визначення функції є відрізок 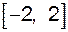 . .
Нехай функція 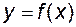 визначена на множині визначена на множині  , а функція , а функція  – на множині – на множині  . Якщо переріз . Якщо переріз  не є порожня множина, то на цьому перерізі можна визначити суму не є порожня множина, то на цьому перерізі можна визначити суму  , різницю , різницю  , добуток , добуток  і частку і частку  двох функцій (останню лише при умові двох функцій (останню лише при умові  ). ).
Графіком функції 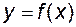 з областю визначення з областю визначення  називається множина всіх точок називається множина всіх точок  площини площини  , координати яких пов’язані даною функціональною залежністю. Найчастіше функція задається на проміжку , координати яких пов’язані даною функціональною залежністю. Найчастіше функція задається на проміжку  , а її графіком буде деяка крива. Проте не слід думати, що графіком щоразу буде деяка крива. Це може бути надто складне геометричне місце точок. , а її графіком буде деяка крива. Проте не слід думати, що графіком щоразу буде деяка крива. Це може бути надто складне геометричне місце точок.
Функція може бути задана одним з основних способів: аналітичним, табличним або графічним. Вважають, що функція 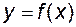 задана аналітично, якщо вона задана за допомогою однієї або кількох формул на різних проміжках. задана аналітично, якщо вона задана за допомогою однієї або кількох формул на різних проміжках.
Нехай на площині дано прямокутну систему координат  . Тоді будь-яка крива в цій площині задає деяку функцію . Тоді будь-яка крива в цій площині задає деяку функцію  від від  , якщо всяка пряма, паралельна осі , якщо всяка пряма, паралельна осі  , перетинає цю криву не більше ніж в одній точці. Це графічний спосіб задання функції. , перетинає цю криву не більше ніж в одній точці. Це графічний спосіб задання функції.
Функцію можна задати і за допомогою таблиці, в одному рядку якої записані значення однієї величини, а в іншому – відповідні значення другої величини, що залежить від першої.
Зауваження. Якщо функція задана аналітично, то неважко перейти до табличного або графічного способу задання функції. Перехід від табличного або графічного способів задання функцій до аналітичного вимагає певних знань та навичок.
Завдання для самостійного розв’язування.
1.1 Знайти область визначення функцій:
а) 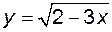 ; б) ; б)  ; ;
в)  ; г) ; г)  ; ;
Відповіді:
1.1 а)  б) б) 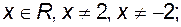
в)  г) г) 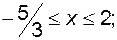
Складена функція.
Нехай функція 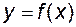 визначена на множині визначена на множині  , а функція , а функція 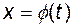 на множині на множині  , причому для всіх , причому для всіх  відповідне значення відповідне значення  належить множині належить множині  . Тоді на множині . Тоді на множині  визначена функція визначена функція  , що називається складеною функцією від , що називається складеною функцією від  , або суперпозицією функцій , або суперпозицією функцій  і і  . .
Наприклад, функція  визначена на множині визначена на множині  , а функція , а функція  визначена на множині визначена на множині 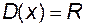 і має область зміни і має область зміни  . Так як множина . Так як множина  , то суперпозиція цих функцій , то суперпозиція цих функцій  визначена на множині визначена на множині  . .
Проте може статись так, що  і і  не мають спільних точок, тоді відповідні функції не мають спільних точок, тоді відповідні функції 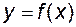 і і 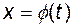 не утворюють суперпозицію. Наприклад, функції не утворюють суперпозицію. Наприклад, функції  і і  такі, що такі, що  і і  не мають ні однієї спільної точки. Таким чином, вираз не мають ні однієї спільної точки. Таким чином, вираз 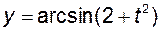 не задає функції від не задає функції від  . .
Обернена функція.
Нехай функція 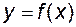 визначена на відрізку визначена на відрізку  , а множиною її значень є відрізок , а множиною її значень є відрізок 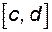 , тобто , тобто  , ,  . .
Якщо кожному значенню  відповідає єдине значення відповідає єдине значення  , для якого , для якого  , то на відрізку , то на відрізку 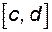 можна визначити функцію можна визначити функцію  , яка називається оберненою по відношенню до функції , яка називається оберненою по відношенню до функції 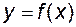 . .
Зауваження. Означення оберненої функції може бути узагальнено і для випадків коли  і і 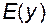 є будь-які проміжки, а не тільки відрізки. є будь-які проміжки, а не тільки відрізки.
Приклад. Функція  визначена на визначена на 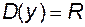 . Оберненою для неї є функція . Оберненою для неї є функція  , що також визначена на , що також визначена на 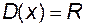 . .
Проте не всяка функція 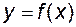 має обернену. Так функція має обернену. Так функція  , оберненої не має, оскільки двом різним точкам , оберненої не має, оскільки двом різним точкам  і і 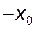 вона ставить у відповідність одну точку вона ставить у відповідність одну точку  . Сформулюємо теорему існування оберненої функції: . Сформулюємо теорему існування оберненої функції:
Теорема. Якщо функція 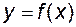 строго монотонна на відрізку строго монотонна на відрізку  , то обернена функція , то обернена функція  існує і строго монотонна на відрізку існує і строго монотонна на відрізку 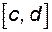 . .
Функція  , має обернену , має обернену  , оскільки кожним двом різним точкам , оскільки кожним двом різним точкам  , вона ставить у відповідність дві різні точки , вона ставить у відповідність дві різні точки  . .
Легко помітити, що  не є монотонною для не є монотонною для  , а функція , а функція  є зростаючою на проміжку є зростаючою на проміжку  . .
Елементарні функції.
Означення. Основні елементарні функції: степенева  , показникова , показникова 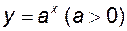 , обернена до степеневої , обернена до степеневої  , логарифмічна , логарифмічна  , тригонометричні , тригонометричні     обернені тригонометричні обернені тригонометричні    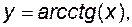 а також функції, знайдені за допомогою формул, що містять скінчене число арифметичних дій (додавання, віднімання, множення, ділення) і суперпозицій основних елементарних функцій, називаються елементарними функціями. а також функції, знайдені за допомогою формул, що містять скінчене число арифметичних дій (додавання, віднімання, множення, ділення) і суперпозицій основних елементарних функцій, називаються елементарними функціями.
З основними елементарними функціями ми познайомились в шкільному курсі математики, а тому їх властивості пропонуємо розглянути самостійно.
§ 2. Послідовність. Границя послідовності.
Функція, задана на множині натуральних чисел, називається числовою послідовністю.
Позначається  де де  – загальний член послідовності. Кожна числова послідовність вважається заданою, якщо вказано правило чи закон її утворення. – загальний член послідовності. Кожна числова послідовність вважається заданою, якщо вказано правило чи закон її утворення.
Наприклад, нехай задано загальний член послідовності 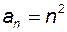 , тоді її членами будуть числа , тоді її членами будуть числа  . Для послідовностей з загальними членами . Для послідовностей з загальними членами 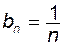 , ,  членами будуть відповідно числа: членами будуть відповідно числа:  та та 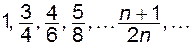
Приклад 2.1. Побудувати числову послідовність для знаходження грошових накопичень з урахуванням складних процентів.
Розв'язок. Нехай початкова сума вкладу складає  грн., процентна ставка дорівнює грн., процентна ставка дорівнює  річних. Величина річних. Величина  називається питомою процентною ставкою. називається питомою процентною ставкою.
На кінець першого року сума вкладу складе  , на кінець другого року – , на кінець другого року –  , на кінець , на кінець  року – року –  . .
Розглянемо послідовності  і і  . Побудуємо точки на числовій осі, що відповідають членам цих послідовностей: . Побудуємо точки на числовій осі, що відповідають членам цих послідовностей:
З рисунку видно, що члени послідовності  по мірі зростання номера по мірі зростання номера  наближаються до точки 0, члени другої послідовності необмежено віддаляються від початку координат. наближаються до точки 0, члени другої послідовності необмежено віддаляються від початку координат.
Виберемо  - окіл точки 0 з - окіл точки 0 з  . Поза цим околом знаходяться десять перших членів, всі інші, тобто всі починаючи з номера . Поза цим околом знаходяться десять перших членів, всі інші, тобто всі починаючи з номера  , належать цьому околу. Виберемо менший окіл точки 0, наприклад , належать цьому околу. Виберемо менший окіл точки 0, наприклад  . Поза цим околом знаходяться перші сто членів, а всі інші, починаючи з номера . Поза цим околом знаходяться перші сто членів, а всі інші, починаючи з номера  , належать вибраному околу. , належать вибраному околу.
Означення 1. Число  називається границею числової послідовності називається границею числової послідовності  , якщо будь-який , якщо будь-який  - окіл точки - окіл точки  містить всі члени послідовності, починаючи з деякого номера містить всі члени послідовності, починаючи з деякого номера 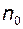 , а поза ним знаходиться фіксоване число членів послідовності. , а поза ним знаходиться фіксоване число членів послідовності.
Якщо члени послідовності належать  - околу точки - околу точки  , то це значить, що для всіх цих членів виконується нерівність , то це значить, що для всіх цих членів виконується нерівність  , або згідно властивості 7 модуля , або згідно властивості 7 модуля  . .
Означення 2. Число  називається границею числової послідовності називається границею числової послідовності  , якщо для будь-якого , якщо для будь-якого  існує такий номер існує такий номер 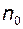 , що для всіх членів послідовності з номерами , що для всіх членів послідовності з номерами  виконується нерівність виконується нерівність
 . (2.1) . (2.1)
Границя числової послідовності позначається 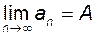 або або  . .
Приклад 2.2 Довести, що для послідовності  , ,   . .
Розв'язування. Для будь-якого  нерівність (2.1) нерівність (2.1) 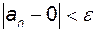 або або  виконується при виконується при  . Отже, при будь-якому . Отже, при будь-якому  існує такий номер існує такий номер 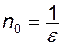 (або рівний цілій частині (або рівний цілій частині 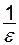 ), що для всіх ), що для всіх  виконується нерівність виконується нерівність  . А це означає, що . А це означає, що  . .
Приклад 2.3 Довести, що послідовність  не має границі. не має границі.
Розв’язування. При будь-якому  два сусідні члени цієї послідовності відрізняються за модулем на 2. Отже для два сусідні члени цієї послідовності відрізняються за модулем на 2. Отже для  на числовій осі не має жодної точки на числовій осі не має жодної точки  - окіл якої містив би усі члени послідовності починаючи з деякого - окіл якої містив би усі члени послідовності починаючи з деякого 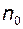 . Це означає, що ні одне дійсне число не може бути границею цієї послідовності. . Це означає, що ні одне дійсне число не може бути границею цієї послідовності.
Послідовності, які мають границю, називаються збіжними, а ті що не мають – розбіжними.
Обмежені послідовності. Зв'язок між існуванням границі та її обмеженістю.
Означення. Послідовність  називається обмеженою, якщо існує таке число називається обмеженою, якщо існує таке число  , що для всіх , що для всіх  виконується нерівність виконується нерівність 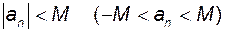 . .
Теорема. Якщо послідовність  має границю, то вона обмежена. має границю, то вона обмежена.
Доведення. Нехай 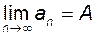 . Для . Для  існує номер такий номер існує номер такий номер 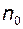 , що для всіх членів послідовності з номерами , що для всіх членів послідовності з номерами  виконується нерівність виконується нерівність  . Виберемо . Виберемо  . Тоді для всіх . Тоді для всіх  виконується нерівність виконується нерівність  , а отже послідовність , а отже послідовність  є обмеженою. є обмеженою.
Зауважимо, що протилежне твердження в цілому не вірне. Наприклад, послідовність  обмежена, але границі не має. обмежена, але границі не має.
Властивості границь.
Властивість 1. Якщо всі члени послідовності дорівнюють  , то і границя цієї послідовності дорівнює , то і границя цієї послідовності дорівнює  . .
Властивість 2. Якщо послідовність  має границю має границю  , то послідовність , то послідовність  – нескінченно мала. – нескінченно мала.
Властивість 3. Якщо послідовність  має границю, то вона єдина. має границю, то вона єдина.
Завдання для самостійного розв’язування.
2.1 Скориставшись означенням границі довести, що
а)  . б) . б)  . .
2.2 Впевнитись, що послідовність  не має границі при необмеженому зростанні не має границі при необмеженому зростанні  . .
Розкриття невизначеностей.
При знаходженні границь функцій (послідовностей) ми користуємось арифметичними теоремами в припущенні, що відповідні границі існують, а для частки з додатковою умовою, що границя знаменника відміна від нуля.
В деяких випадках, що залишились без розгляду (коли границі функцій (одна або обидві) нескінченні чи не існують, або у випадку частки - границя знаменника дорівнює нулю) можна цілком визначено сказати як поводить себе відповідна функція. Наприклад, якщо  , ,  , ,  , то , то  , ,  , , 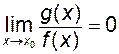 , ,  . .
Проте, якщо  , то про границю частки , то про границю частки  ніякого загального твердження ми зробити не можемо. Наприклад, нехай ніякого загального твердження ми зробити не можемо. Наприклад, нехай  , ,  . Обидві функції при . Обидві функції при  прямують до нуля. Їх відношення прямують до нуля. Їх відношення  також прямує до нуля, коли також прямує до нуля, коли  . Якщо ж, навпаки, . Якщо ж, навпаки,  , ,  , то , то 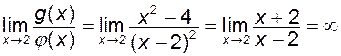 . Отже, в залежності від вигляду обох функцій, границя частки може існувати, а може і не існувати. В зв’язку з цим говорять, що мають справу з невизначеністю. А задача знаходження границі в кожному такому випадку називається задачею розкриття невизначеності. Розглянемо найбільш важливі випадки: . Отже, в залежності від вигляду обох функцій, границя частки може існувати, а може і не існувати. В зв’язку з цим говорять, що мають справу з невизначеністю. А задача знаходження границі в кожному такому випадку називається задачею розкриття невизначеності. Розглянемо найбільш важливі випадки:
а) невизначеність  . .
Якщо  і і  , то у випадку знаходження границі частки , то у випадку знаходження границі частки  ми маємо невизначеність ми маємо невизначеність  . У випадку, коли функції . У випадку, коли функції 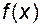 та та  є алгебраїчними, то для розкриття невизначеності в чисельнику і знаменнику слід виділити множник є алгебраїчними, то для розкриття невизначеності в чисельнику і знаменнику слід виділити множник  , щоб в подальшому скоротити дріб на цей множник: , щоб в подальшому скоротити дріб на цей множник:
1)  . .
2) 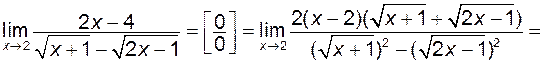
 . .
В другому прикладі для виділення множника  знищили ірраціональність в знаменнику шляхом домноження на спряжений вираз. знищили ірраціональність в знаменнику шляхом домноження на спряжений вираз.
б) невизначеність  . .
Нехай  , ,  при при  . В цьому випадку вираз . В цьому випадку вираз  називають невизначеністю називають невизначеністю  . Як приклад розглянемо відношення двох многочленів. Вираз . Як приклад розглянемо відношення двох многочленів. Вираз  , ,  , ,  - ціле невід'ємне число, називається многочленом. Перший доданок - ціле невід'ємне число, називається многочленом. Перший доданок  називається старшим членом, називається старшим членом,  - степенем многочлена. Поведінка многочлена, коли - степенем многочлена. Поведінка многочлена, коли  визначається поведінкою старшого члена, тобто визначається поведінкою старшого члена, тобто  . Тому: . Тому:
1)  , ,
2)  , ,
3)  . .
Наведені приклади можна об'єднати в загальне правило:
границя відношення двох многочленів дорівнює  , якщо степінь чисельника більший степеня знаменника; дорівнює 0, якщо степінь чисельника менший степеня знаменника, і дорівнює відношенню коефіцієнтів при старших членах, якщо степені чисельника і знаменника рівні, тобто , якщо степінь чисельника більший степеня знаменника; дорівнює 0, якщо степінь чисельника менший степеня знаменника, і дорівнює відношенню коефіцієнтів при старших членах, якщо степені чисельника і знаменника рівні, тобто
 , ,
де  степені многочленів степені многочленів  відповідно. відповідно.
в) невизначеність  . .
Нехай  , ,  при при  . Тоді вираз . Тоді вираз  дає невизначеність дає невизначеність  . Щоб розкрити невизначеність такого вигляду, потрібно звести її до невизначеностей вигляду . Щоб розкрити невизначеність такого вигляду, потрібно звести її до невизначеностей вигляду  або або  . .
Приклад 3.3 Знайти  . .
Розв’язування. 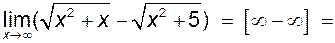
 . .
г) невизначеність  . .
Розглянемо  . Якщо . Якщо  , ,  при при  , то вираз , то вираз  дає невизначеність дає невизначеність  . Щоб розкрити невизначеність даного вигляду, як і у попередньому випадку слід звести її до невизначеностей вигляду . Щоб розкрити невизначеність даного вигляду, як і у попередньому випадку слід звести її до невизначеностей вигляду  або або  . .
Завдання для самостійного розв’язування.
3.1 Знайти границі:
а)  ; б) ; б)  ; ;
в)  ; г) ; г)  ; ;
д)  ; е) ; е)  . .
3.2 Знайти границі:
а)  ; б) ; б)  ; ;
в)  ; г) ; г)  ; ;
д).  ; е) ; е)  . .
3.3 Знайти границі:
а)  ; б) ; б)  ; ;
в)  ; г) ; г)  ; ;
д)  ; е) ; е)  ; ;
є)  ; ж) ; ж)  . .
3.4 Знайти границі:
а)  ; б) ; б)  ; ;
в)  ; г) ; г)  ; ;
д)  ; е) ; е)  . .
Відповіді:
3.1 а)  б) б)  в) в)  г) г)  д) 0; е) 6; д) 0; е) 6;
3.2 а) 0; б)  ; в) ; в)  ; г) ; г)  д) д)  е) е) 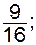
3.3 а)  ; б) ; б)  в) в)  г) г)  д) д)  е) -5; е) -5;
є)  ; ж) ; ж)  ; ;
3.4 а)  б) б)  в) в)  г) г)  д) -1; е) 0; д) -1; е) 0;
Чудові границі.
1) В попередньому параграфі було встановлено, що  . Розглянемо функцію . Розглянемо функцію  . Ця функція існує для всіх . Ця функція існує для всіх  крім крім  . Можна довести, що . Можна довести, що  . Слід звернути увагу на те, що основа степеня . Слід звернути увагу на те, що основа степеня  при при  , а показник степеня , а показник степеня  . Тобто вираз . Тобто вираз  дає невизначеність дає невизначеність  . .
Поклавши  , знайдемо , знайдемо  . При . При   . У результаті отримаємо ще один запис числа . У результаті отримаємо ще один запис числа  : :  . Обидва розглянутих співвідношення носять назву першої чудової границі і можуть бути використані для розкриття невизначеності . Обидва розглянутих співвідношення носять назву першої чудової границі і можуть бути використані для розкриття невизначеності  . На практиці широко використовують формулу: . На практиці широко використовують формулу:
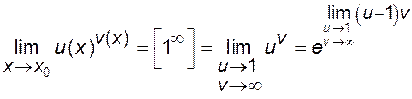
Приклад 3.4 Знайти:
а)  ; б) ; б)  . .
Розв’язування.
а)  . .
б) 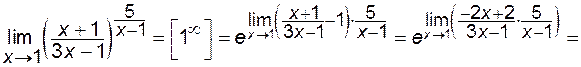
 . .
2) Другою чудовою границею називається  . Скориставшись даним співвідношенням, можна довести, що . Скориставшись даним співвідношенням, можна довести, що
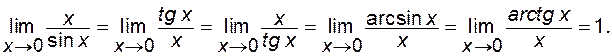
В усіх цих співвідношеннях розглядається відношення двох нескінченно малих величин при умові, що  . Отже всі вони можуть бути використані для розкриття невизначеностей . Отже всі вони можуть бути використані для розкриття невизначеностей  , в яких містяться тригонометричні або обернені тригонометричні функції. , в яких містяться тригонометричні або обернені тригонометричні функції.
Приклад 3.5 Знайти
а)  ; б) ; б)  . .
Розв’язування.
а)  . .
б)  . .
Завдання для самостійного розв’язування.
3.5 Знайти границі:
а)  ; б) ; б) 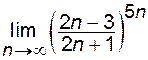 ; ;
в)  ; г) ; г)  ; ;
д) 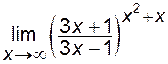 ; е) ; е)  ; ;
є)  ; ж) ; ж)  . .
3.6 Знайти границі:
а)  ; б) ; б)  ; ;
в)  ; г) ; г)  ; ;
д).  ; е) ; е)  ; ;
є)  . ж) . ж)  . .
Відповіді:
3.5 а)  ; б) ; б)  ; в) 1; г) ; в) 1; г)  ; д) ; д)  ; е) ; е)  ; ;
є)  ; ж) e. ; ж) e.
3.6 а)  ; б) ; б)  ; в) 2; г) ; в) 2; г)  ; д) ; д)  ; е) 8; ; е) 8;
є) 8; ж) 1.
§ 4. Неперервність функції.
З поняттям границі функції тісно пов’язано і інше важливе поняття математичного аналізу – поняття неперервності функції. Інтуїтивно поняття неперервності функції пов’язано з графіком функції: функція вважається неперервною, якщо її графік можна провести лінією, не відриваючи олівця від паперу. Що ж станеться, якщо зробити в якійсь точці "прокол"? Тоді перпендикуляр, проведений з цієї точки на ось абсцис, не перетне графіка функції, що рівносильно відсутності значення функції в цій точці. Отже перший висновок: неперервна функція повинна мати значення в точці  . Нехай тепер, підходячи до точки . Нехай тепер, підходячи до точки  з різних сторін, ми залишаємось на "різних рівнях". І в цьому випадку, переходячи через точку з різних сторін, ми залишаємось на "різних рівнях". І в цьому випадку, переходячи через точку  ми відриваємо олівець від паперу. Раніше говорилось, що для існування границі функції в точ ми відриваємо олівець від паперу. Раніше говорилось, що для існування границі функції в точ
|



 – деяка множина дійсних чисел, то запис
– деяка множина дійсних чисел, то запис  означає, що число
означає, що число  належить
належить 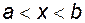 (
( ), де
), де  – фіксовані числа, називається інтервалом (відрізком) і позначається
– фіксовані числа, називається інтервалом (відрізком) і позначається  (
( ).
). або
або  , називається півінтервалом.
, називається півінтервалом. немає суттєвого значення, інтервал, відрізок, півінтервал будемо називати проміжком і позначати
немає суттєвого значення, інтервал, відрізок, півінтервал будемо називати проміжком і позначати  .
. ,
,  називається
називається  – околом точки
– околом точки  .
. – модуль числа.
– модуль числа.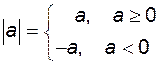
 .
. 2.
2. 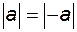
 4.
4. 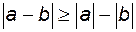
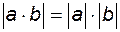 6.
6. 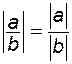
 означає, що
означає, що 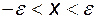 .
. , якщо кожному
, якщо кожному  і записують
і записують 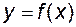 . При цьому
. При цьому  або
або  ,
,  всіх таких значень – областю значень функції і позначається
всіх таких значень – областю значень функції і позначається  або
або 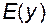 .
.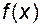 має значення, то таку область визначення будемо називати максимальною областю визначення або областю існування. В подальших прикладах знаходження області визначення функції пов’язане тільки із знаходженням області існування.
має значення, то таку область визначення будемо називати максимальною областю визначення або областю існування. В подальших прикладах знаходження області визначення функції пов’язане тільки із знаходженням області існування. .
. має сенс тоді і тільки тоді, коли
має сенс тоді і тільки тоді, коли  , або
, або 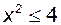 . Так як
. Так як  , то
, то  . Згідно властивості 7 модуля
. Згідно властивості 7 модуля  . Отже, область визначення функції є відрізок
. Отже, область визначення функції є відрізок 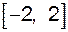 .
. – на множині
– на множині  . Якщо переріз
. Якщо переріз  не є порожня множина, то на цьому перерізі можна визначити суму
не є порожня множина, то на цьому перерізі можна визначити суму  , різницю
, різницю  , добуток
, добуток  і частку
і частку  двох функцій (останню лише при умові
двох функцій (останню лише при умові  ).
). площини
площини  , координати яких пов’язані даною функціональною залежністю. Найчастіше функція задається на проміжку
, координати яких пов’язані даною функціональною залежністю. Найчастіше функція задається на проміжку  , перетинає цю криву не більше ніж в одній точці. Це графічний спосіб задання функції.
, перетинає цю криву не більше ніж в одній точці. Це графічний спосіб задання функції.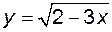 ; б)
; б)  ;
; ; г)
; г)  ;
; б)
б) 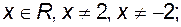
 г)
г) 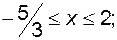
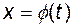 на множині
на множині  , причому для всіх
, причому для всіх  відповідне значення
відповідне значення  належить множині
належить множині  , що називається складеною функцією від
, що називається складеною функцією від  , або суперпозицією функцій
, або суперпозицією функцій  і
і  визначена на множині
визначена на множині  , а функція
, а функція  визначена на множині
визначена на множині 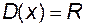 і має область зміни
і має область зміни  . Так як множина
. Так як множина  , то суперпозиція цих функцій
, то суперпозиція цих функцій  визначена на множині
визначена на множині  .
. не мають спільних точок, тоді відповідні функції
не мають спільних точок, тоді відповідні функції  і
і  такі, що
такі, що  і
і  не мають ні однієї спільної точки. Таким чином, вираз
не мають ні однієї спільної точки. Таким чином, вираз 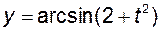 не задає функції від
не задає функції від 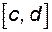 , тобто
, тобто  ,
,  .
. відповідає єдине значення
відповідає єдине значення  , для якого
, для якого  , то на відрізку
, то на відрізку  , яка називається оберненою по відношенню до функції
, яка називається оберненою по відношенню до функції  визначена на
визначена на 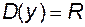 . Оберненою для неї є функція
. Оберненою для неї є функція  , що також визначена на
, що також визначена на  , оберненої не має, оскільки двом різним точкам
, оберненої не має, оскільки двом різним точкам  і
і 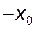 вона ставить у відповідність одну точку
вона ставить у відповідність одну точку  . Сформулюємо теорему існування оберненої функції:
. Сформулюємо теорему існування оберненої функції: , має обернену
, має обернену  , оскільки кожним двом різним точкам
, оскільки кожним двом різним точкам  , вона ставить у відповідність дві різні точки
, вона ставить у відповідність дві різні точки  .
. , а функція
, а функція  .
. , показникова
, показникова 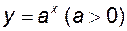 , обернена до степеневої
, обернена до степеневої  , логарифмічна
, логарифмічна  , тригонометричні
, тригонометричні 


 обернені тригонометричні
обернені тригонометричні 


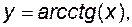 а також функції, знайдені за допомогою формул, що містять скінчене число арифметичних дій (додавання, віднімання, множення, ділення) і суперпозицій основних елементарних функцій, називаються елементарними функціями.
а також функції, знайдені за допомогою формул, що містять скінчене число арифметичних дій (додавання, віднімання, множення, ділення) і суперпозицій основних елементарних функцій, називаються елементарними функціями. де
де  – загальний член послідовності. Кожна числова послідовність вважається заданою, якщо вказано правило чи закон її утворення.
– загальний член послідовності. Кожна числова послідовність вважається заданою, якщо вказано правило чи закон її утворення.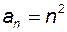 , тоді її членами будуть числа
, тоді її членами будуть числа  . Для послідовностей з загальними членами
. Для послідовностей з загальними членами 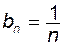 ,
,  членами будуть відповідно числа:
членами будуть відповідно числа:  та
та 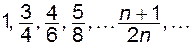
 грн., процентна ставка дорівнює
грн., процентна ставка дорівнює  річних. Величина
річних. Величина  називається питомою процентною ставкою.
називається питомою процентною ставкою. , на кінець другого року –
, на кінець другого року –  , на кінець
, на кінець  року –
року –  .
. і
і  . Побудуємо точки на числовій осі, що відповідають членам цих послідовностей:
. Побудуємо точки на числовій осі, що відповідають членам цих послідовностей: наближаються до точки 0, члени другої послідовності необмежено віддаляються від початку координат.
наближаються до точки 0, члени другої послідовності необмежено віддаляються від початку координат. . Поза цим околом знаходяться десять перших членів, всі інші, тобто всі починаючи з номера
. Поза цим околом знаходяться десять перших членів, всі інші, тобто всі починаючи з номера  , належать цьому околу. Виберемо менший окіл точки 0, наприклад
, належать цьому околу. Виберемо менший окіл точки 0, наприклад  . Поза цим околом знаходяться перші сто членів, а всі інші, починаючи з номера
. Поза цим околом знаходяться перші сто членів, а всі інші, починаючи з номера  , належать вибраному околу.
, належать вибраному околу.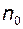 , а поза ним знаходиться фіксоване число членів послідовності.
, а поза ним знаходиться фіксоване число членів послідовності. , або згідно властивості 7 модуля
, або згідно властивості 7 модуля  .
. існує такий номер
існує такий номер  виконується нерівність
виконується нерівність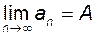 або
або  .
.
 .
.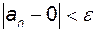 або
або  виконується при
виконується при  . Отже, при будь-якому
. Отже, при будь-якому 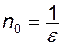 (або рівний цілій частині
(або рівний цілій частині 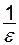 ), що для всіх
), що для всіх  . А це означає, що
. А це означає, що  .
. не має границі.
не має границі. на числовій осі не має жодної точки
на числовій осі не має жодної точки  , що для всіх
, що для всіх  виконується нерівність
виконується нерівність 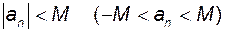 .
. . Тоді для всіх
. Тоді для всіх  , а отже послідовність
, а отже послідовність  має границю
має границю  – нескінченно мала.
– нескінченно мала. . б)
. б)  .
. не має границі при необмеженому зростанні
не має границі при необмеженому зростанні  ,
,  ,
,  , то
, то  ,
,  ,
, 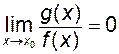 ,
,  .
. , то про границю частки
, то про границю частки  ніякого загального твердження ми зробити не можемо. Наприклад, нехай
ніякого загального твердження ми зробити не можемо. Наприклад, нехай  ,
,  . Обидві функції при
. Обидві функції при  прямують до нуля. Їх відношення
прямують до нуля. Їх відношення  також прямує до нуля, коли
також прямує до нуля, коли  . Якщо ж, навпаки,
. Якщо ж, навпаки,  ,
,  , то
, то 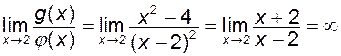 . Отже, в залежності від вигляду обох функцій, границя частки може існувати, а може і не існувати. В зв’язку з цим говорять, що мають справу з невизначеністю. А задача знаходження границі в кожному такому випадку називається задачею розкриття невизначеності. Розглянемо найбільш важливі випадки:
. Отже, в залежності від вигляду обох функцій, границя частки може існувати, а може і не існувати. В зв’язку з цим говорять, що мають справу з невизначеністю. А задача знаходження границі в кожному такому випадку називається задачею розкриття невизначеності. Розглянемо найбільш важливі випадки: .
. і
і  є алгебраїчними, то для розкриття невизначеності в чисельнику і знаменнику слід виділити множник
є алгебраїчними, то для розкриття невизначеності в чисельнику і знаменнику слід виділити множник  , щоб в подальшому скоротити дріб на цей множник:
, щоб в подальшому скоротити дріб на цей множник: .
.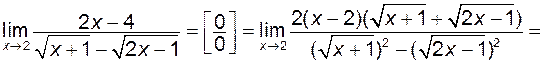
 .
. знищили ірраціональність в знаменнику шляхом домноження на спряжений вираз.
знищили ірраціональність в знаменнику шляхом домноження на спряжений вираз. .
. ,
,  при
при  . В цьому випадку вираз
. В цьому випадку вираз  ,
,  ,
,  називається старшим членом,
називається старшим членом,  визначається поведінкою старшого члена, тобто
визначається поведінкою старшого члена, тобто  . Тому:
. Тому: ,
, ,
, .
. , якщо степінь чисельника більший степеня знаменника; дорівнює 0, якщо степінь чисельника менший степеня знаменника, і дорівнює відношенню коефіцієнтів при старших членах, якщо степені чисельника і знаменника рівні, тобто
, якщо степінь чисельника більший степеня знаменника; дорівнює 0, якщо степінь чисельника менший степеня знаменника, і дорівнює відношенню коефіцієнтів при старших членах, якщо степені чисельника і знаменника рівні, тобто ,
, степені многочленів
степені многочленів  відповідно.
відповідно. .
. . Тоді вираз
. Тоді вираз  .
.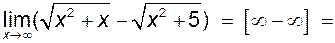
 .
. .
. . Якщо
. Якщо  при
при  , то вираз
, то вираз  ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  ;
; ; ж)
; ж)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  .
. б)
б)  в)
в)  г)
г)  д) 0; е) 6;
д) 0; е) 6; ; г)
; г)  д)
д)  е)
е) 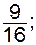
 ; б)
; б)  в)
в)  г)
г)  д)
д)  е) -5;
е) -5; б)
б)  . Розглянемо функцію
. Розглянемо функцію  . Ця функція існує для всіх
. Ця функція існує для всіх  крім
крім  . Можна довести, що
. Можна довести, що  . Слід звернути увагу на те, що основа степеня
. Слід звернути увагу на те, що основа степеня  при
при  , а показник степеня
, а показник степеня  дає невизначеність
дає невизначеність  .
. , знайдемо
, знайдемо  . При
. При  . У результаті отримаємо ще один запис числа
. У результаті отримаємо ще один запис числа  :
:  . Обидва розглянутих співвідношення носять назву першої чудової границі і можуть бути використані для розкриття невизначеності
. Обидва розглянутих співвідношення носять назву першої чудової границі і можуть бути використані для розкриття невизначеності 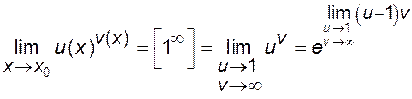
 ; б)
; б)  .
. .
.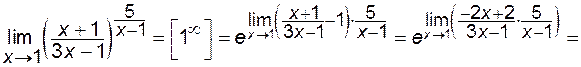
 .
. . Скориставшись даним співвідношенням, можна довести, що
. Скориставшись даним співвідношенням, можна довести, що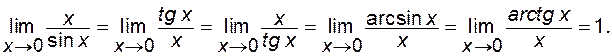
 . Отже всі вони можуть бути використані для розкриття невизначеностей
. Отже всі вони можуть бути використані для розкриття невизначеностей  ; б)
; б)  .
. .
. .
. ; б)
; б) 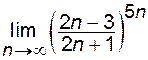 ;
; ; г)
; г)  ;
;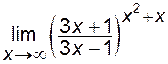 ; е)
; е)  ;
; ; ж)
; ж)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  ;
; . ж)
. ж)  .
. ; б)
; б)  ; в) 1; г)
; в) 1; г)  ;
; ; ж) e.
; ж) e. ; б)
; б)  ; в) 2; г)
; в) 2; г)  ; д)
; д)  ; е) 8;
; е) 8;


