
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальне числення функції багатьох змінних ⇐ ПредыдущаяСтр 4 из 4
Література [5] – с. 499-574, [6] – с. 341-407, [7] – с. 284-329. Якщо кожній точці
де Зокрема, коли Позначимо частинні прирости функції
Якщо існують скінченні границі
то їх називають частинними похідними функції Позначення: Правило знаходження частинних похідних першого порядку: Для обчислення частинних похідних
Приклад 1. Знайти частинні похідні функції
Розв’язання. Функція визначена в області
Вважаючи, що
Функція
де Повним диференціалом першого порядку
Так як Теорема. Якщо функція
Отже повний диференціал функції
При досить малих Приклад 2 Задана функція 1) Обчислити значення 2) Обчислити наближене значення 3) Знайти відносну похибку (у відсотках) при заміні приросту 4) Написати рівняння дотичної площини до поверхні Розв’язання. 1) Обчислимо значення
2) Обчислимо наближене значення
Підставимо знайдені значення у формулу (1):
3) Знайдемо відносну похибку при заміні приросту
4) Знайдемо рівняння дотичної площини до поверхні
Нехай функція
то ця границя називається похідною функції
Похідна за напрямом Якщо функція
де
Приклад 3 Знайти похідну скалярного поля Розв’язання. Знайдемо нормальний вектор
Отже нормальний вектор до поверхні Скористаємось формулою (2) для обчислення похідної за напрямом. Знайдемо напрямні косинуси вектора
Обчислимо значення частинних похідних у точці
Отже
Вектор, координатами якого є значення частинних похідних функції
Вектор градієнта вказує напрямок найшвидшого зростання функції. Завдання: Таблиця вибору варіантів:
Завдання до виконання: 1.Обчислити похідну за напрямом вектора М1М2 та градієнт в точці М1, якщо М1(а;в), а М2(в;-с) 1. 2 3. 2.Обчислити похідну за напрямом градієнта в точці М(с;-а)
Контрольні запитання: 1. Як знайти частинні похідні першого порядку? 2. Що таке похідна за напрямом? 3. Формула для знаходження градієнта. 4. Що характеризують градієнт та похідну за напрямом?
Практична робота № 14
Тема: Застосування повного диференціала до наближених обчислень Мета: Навчитись обчислювати наближені значення функції, використовуючи повний диференціал. Теоретичні відомості: Функція
де Повним диференціалом першого порядку
Так як Теорема. Якщо функція
Отже повний диференціал функції
При досить малих
Приклади розв’язання завдань: Приклад. Задана функція 5) Обчислити значення 6) Обчислити наближене значення 7) Знайти відносну похибку (у відсотках) при заміні приросту Розв’язання. 1) Обчислимо значення
2) Обчислимо наближене значення
Підставимо знайдені значення у формулу (1):
3) Знайдемо відносну похибку при заміні приросту
Завдання до виконання:
Задана функція 1) Обчислити значення 2) Обчислити наближене значення 3) Знайти відносну похибку (у відсотках) при заміні приросту Вказівка: т. А – добирати самостійно, виходячи з умови 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Контрольні запитання: 1. Дати означення функції багатьох змінних. 2. Дати означення повного диференціала. 3. Записати формулу для обчислення повного диференціала. Практична робота № 15. Тема: Дослідження рядів на збіжність. Розклад функцій в степеневі ряди Тейлора-Маклорена. Мета: Навчитися застосовувати ознаки збіжності рядів до дослідження рядів на збіжність. Навчитися розкладати функції в степеневі ряди Тейлора-Маклорена Література: [4] – с. 254-259; [1] – с. 493-497; [5] – с. 249-256. с. 295-261; [1] – с. 498-499; [5] – с. 257-259.
Теоретичні відомості:
Нехай задано нескінченну послідовність чисел
Вираз
Якщо послідовність частинних сум Якщо послідовність Необхідна умова збіжності ряду. Якщо ряд
Наслідок. Якщо
Достатні умови збіжності ряду: І. Ознаки порівняння. 1. Перша ознака порівняння. Нехай задано два знакододатні ряди
Якщо ряд Якщо ряд 2. Друга ознака порівняння. Якщо задано два знакододатні ряди
причому існує скінчена границя Ознака Д’Аламбера. Якщо для знакододатного ряду
то 1) цей ряд збіжний при 2) цей ряд розбіжний при Радикальна ознака Коші. Якщо для знакододатного ряду 1) ряд збіжний при 2) ряд розбіжний при
Інтегральна ознака Коші. Нехай функція
Числовий ряд, члени якого можуть бути як додатними, так і від’ємними називається знакозмінним. Теорема Лейбніца. Знакозмінний ряд 1) 2) При цьому сума додатна і не перевищує першого його члена.
Знакозмінний ряд Якщо знакозмінний ряд Ряд Функціональний ряд виду де Інтервалом збіжності степеневого ряду Радіус збіжності степеневого ряду можна знайти за формулами:
Розклади основних елементарних функцій в степеневі ряди Маклорена:
Приклади розв’язання рівнянь: Приклад 1. Дослідити на збіжність ряд Розв’язання. Застосуємо ознаку порівняння. Порівнюємо з рядом Приклад 2. Застосовуючи ознаку Д’Аламбера, дослідити на збіжність ряд Розв’язання.
Заданий ряд розбіжний.
Завдання до виконання:
1. Дослідити ряди на збіжність
1.
5.
9.
13. 2.Розкласти функцію
1.
4.
7.
10. Контрольні запитання: 1. Дати означення числового ряда. 2. Дати означення функціонального ряда. 3. Дати означення степеневого ряда.
4. Сформулювати необхідну ознаку збіжності рядів. 5. Сформулювати достатню ознаку збіжності рядів. 6. Записати загальний вигляд ряда Тейлора – Маклорена. 7. Записати формули для обчислення радіусу збіжності степеневого ряду. 8. Навести розклад елементарних функцій в ряд Тейлора – Маклорена. Література:
1. И.И.Валуцэ, Г.Д. Дилигул. Математика для техникумов.Москва. «Наука», 1989г. 2. Вища математика. П.П. Овчинников та ін. Ч.1.Київ «Техніка», 2003р. 3. А.М. Самойленко, С.А. Кривошея, А.М. Самойленко, С.А. Кривошея, Н.А. Перестюк. Дифференциальные уравнения. Примеры и задачи.-Москва, «Высшая школа», 1989г. 4. П.Е.Данко, А.Г.Попов, Т.Я. Кожевникова. Высшая математика в упражнениях и задачах.-Москва «Высшая школа», 1980г. 5. Л.І.Дюженкова, Т.В.Колесник, М.Я. Ляшенко, Г.О.Михалін, М.І.Шкіль, Математичний аналіз у задачах і прикладах. В 2 частинах.-Київ, «Вища школа»,2003р. 6. Навчально – методичні матеріали до виконання контрольних робіт з вищої математики. Ч.1 / Грижук О.П. та ін. – Черкаси, ЧДТУ, 2004 р.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.248.208 (0.161 с.) |
 множини
множини 
 -вимірного простору
-вимірного простору  за деяким законом поставлено у відповідність одне і тільки одне дійсне число
за деяким законом поставлено у відповідність одне і тільки одне дійсне число  , то говорять, що в області
, то говорять, що в області  задано функцію
задано функцію  ,
, – область значень функції.
– область значень функції. , маємо функцію двох змінних
, маємо функцію двох змінних  , якщо кожній парі
, якщо кожній парі  на площині поставлено у відповідність одне і тільки одне число
на площині поставлено у відповідність одне і тільки одне число 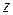 .
. ,
,  .
.
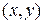 відповідно за змінними
відповідно за змінними  та
та 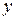 .
. або
або  .
.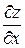
 користуються відомими формулами і правилами диференціювання функції однієї змінної, вважаючи всі змінні, крім
користуються відомими формулами і правилами диференціювання функції однієї змінної, вважаючи всі змінні, крім  , сталими.
, сталими.
 . Вважаючи, що
. Вважаючи, що 

 , якщо її повний приріст
, якщо її повний приріст  можна подати у вигляді
можна подати у вигляді

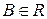 ;
;  – нескінченно малі при
– нескінченно малі при 
 функції
функції  називається головна лінійна відносно
називається головна лінійна відносно  та
та 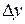 частина повного приросту функції:
частина повного приросту функції:
 ,
,  .
. , то в точці
, то в точці  існують частинні похідні, причому
існують частинні похідні, причому

 має місце наближена формула
має місце наближена формула і точки
і точки 
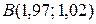 .
.
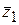 за допомогою повного диференціала;
за допомогою повного диференціала;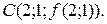


 за допомогою повного диференціала. Нехай
за допомогою повного диференціала. Нехай 
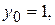



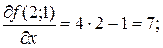





 За попередніми обчисленнями
За попередніми обчисленнями 
 Тоді рівняння дотичної площини має вигляд
Тоді рівняння дотичної площини має вигляд

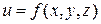 визначена в деякому околі точки
визначена в деякому околі точки  ,
,  – вектор з початком у точці
– вектор з початком у точці  – точка околу, що лежить на векторі
– точка околу, що лежить на векторі  – довжина відрізка
– довжина відрізка  Якщо існує
Якщо існує
 у точці
у точці  , тобто
, тобто
 характеризує швидкість зміни функції
характеризує швидкість зміни функції  , причому
, причому (2)
(2)


 в точці
в точці  за напрямом тої нормалі до поверхні
за напрямом тої нормалі до поверхні  , яка утворює гострий кут з додатнім напрямком осі
, яка утворює гострий кут з додатнім напрямком осі  .
.  ,
, 
 .
. .
.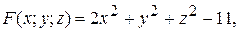


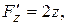



 Координата z вектора
Координата z вектора  додатна (z=6), тому нормаль до поверхні
додатна (z=6), тому нормаль до поверхні 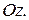
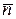 :
:






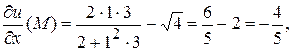



 , називають градієнтом функції в цій точці і позначають
, називають градієнтом функції в цій точці і позначають  :
:

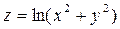




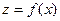 і точки А(x;y) i
і точки А(x;y) i  , В(0,98;5,02)
, В(0,98;5,02) , В(1,92;-2,38)
, В(1,92;-2,38)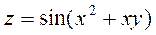 , В(2,32;-5,003)
, В(2,32;-5,003) , В(4,08;-1,93)
, В(4,08;-1,93) , В(3,99;8,02)
, В(3,99;8,02) , В(-3,87;4,02)
, В(-3,87;4,02)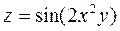 , В(1,96;5,004)
, В(1,96;5,004) , В(2,02;8,009)
, В(2,02;8,009) , В(6,99;2,23)
, В(6,99;2,23)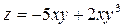 ,В(2,96;7,02)
,В(2,96;7,02) .
. (1) називається числовим рядом.
(1) називається числовим рядом. збіжна і
збіжна і  , то число
, то число  називається сумою ряду (1), а ряд називається збіжним.
називається сумою ряду (1), а ряд називається збіжним. збіжний, то
збіжний, то .
. , то ряд
, то ряд  ,
,  і
і 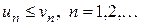 .
. і ця границя не дорівнює 0, то ці ряди збіжні або розбіжні одночасно.
і ця границя не дорівнює 0, то ці ряди збіжні або розбіжні одночасно. ) існує границя
) існує границя ,
, ;
; .
. , то
, то , визначена на проміжку
, визначена на проміжку  є додатною та не зростаючою на цьому проміжку. Тоді невласний інтеграл
є додатною та не зростаючою на цьому проміжку. Тоді невласний інтеграл  збіжний (розбіжний) одночасно із знакододатнім числовим рядом
збіжний (розбіжний) одночасно із знакододатнім числовим рядом .
. збіжний, якщо
збіжний, якщо
 .
. називається абсолютно збіжним, якщо ряд
називається абсолютно збіжним, якщо ряд  , складений з модулів його членів, є збіжним.
, складений з модулів його членів, є збіжним. , членами якого є функції, визначені на деякій множині
, членами якого є функції, визначені на деякій множині  ,
, – дійсні числа, називають степеневим рядом.
– дійсні числа, називають степеневим рядом. називають такий інтервал
називають такий інтервал  , що для кожної точки
, що для кожної точки  називають радіусом збіжності степеневого ряду.
називають радіусом збіжності степеневого ряду.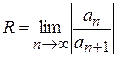 , або
, або  .
.


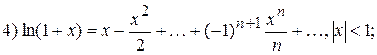

 .
. , який збіжний, так як його члени утворюють геометричну прогресію із знаменником
, який збіжний, так як його члени утворюють геометричну прогресію із знаменником  , а оскільки
, а оскільки  то ряд
то ряд  – теж збіжний.
– теж збіжний. .
.

 2.
2.  3.
3.  4.
4. 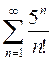
 6.
6.  7.
7.  8.
8. 
 10.
10.  11.
11. 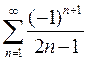 12.
12. 
 14.
14.  15.
15. 

 в ряд Тейлора-Маклорена
в ряд Тейлора-Маклорена 2.
2.  3.
3. 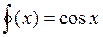
 5.
5. 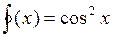 6.
6. 
 8.
8.  9.
9. 




