
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад 1. Розв’язати систему лінійних рівняньСодержание книги
Поиск на нашем сайте
трьома способами: а) методом Крамера; б) матричним способом; в) методом Гаусса. Розв’язання. Обчислимо визначник системи:
а) Знайдемо
Підставляючи знайдені значення визначників у формули Крамера (4) отримаємо
б) Знайдемо розв’язок матричним способом. Відповідно до введених позначень маємо
Використаємо отримане в попередньому пункті значення визначника матриці
Для знаходження оберненої матриці
Згідно формули (1)
Розв’язок системи знайдемо за формулою (3):
Завдання до виконання:
1.Знайти значення матричного многочлена 5AB + 2B2; 2.Транспонувати матрицю В; 3.Знайти матрицю А-1
1. А= 2. А= 3. А= 4. А= 5. А= 6. А= 7. А= 8. А= 9. А= 10. А= 11. А= 12. А= 13. А= 14. А= 15. А= 16. А= 17. А= 18. А= 19. А= 20. А= 21. А= 22. А= 23. А= 24. А= 25. А= 26. А= 27. А= 28. А= 29. А= 30. А=
Контрольні запитання: 1. Що таке матриця? 2. Як додати матриці? 3. Записати формулу множення матриць? 4. В чому полягає метод Гауса? 5. В чому полягає метод Крамера? 6. Записати формули для розв’язання системи лінійних рівнянь матричним способом. 7. Яка матриця називається транспонованою?
Практична робота № 3 Тема: Рівняння прямої на площині. Мета: Систематизувати набуті знання. Вміти розрізняти різні форми прямої на площині та вміти їх записувати. Навчитися відшукувати вірний підхід до розв’язання тієї чи іншої задачі. Література: [1] – с. 140-144; [2] – с. 8-13, 37-48; [4] – с. 58-65; [5] – с. 23-51. Теоретичні відомості Пряма на площині. 1. Пряма, що проходить через точку
Позначимо
2.
Рівняння (6) називають канонічним рівнянням прямої. 3. Пряма, що проходить через дві точки
Відстань від точки
Приклад 2. (Задача 2.2.) Дано вершини трикутника 1) рівняння сторін 2) рівняння медіани 3) рівняння прямої, що проходить через точку Розв’язання. 1) Запишемо рівняння прямої, що проходить через дві точки (7)
Отримали канонічне рівняння прямої (6), з якого встановимо, що
Маємо загальне рівняння прямої, з якого Аналогічно отримаємо рівняння інших сторін
2)
Медіана
Складемо рівняння прямої, що проходить через дві точки
3) Пряма
Оскільки прямі
Завдання до виконання: Оберіть значення для виконання завдань згідно таблиці: П – номер студента в друкованому списку журналу.
1. Заданий трикутник АВС. Знайти: · Довжину та рівняння сторони АВ; · Рівняння прямої, що проходить через точку В перпендикулярно медіані ВМ; · Написати рівняння висоти та медіани, проведених з точки А; · Знайти кути трикутника. 2. Знайти четверту вершину паралелограма АВСК та його гострий кут. 3. Дослідити взаємне розташування прямих
(а-в)х+(с-2в)у=8 3сх-2ау=11 4. Написати висновок. Контрольні запитання 1. Записати рівняння прямої, що проходить через 2 точки. 2. Записати рівняння прямої, що проходить через точку А перпендикулярно заданому вектору. 3. Записати канонічне рівняння прямої. 4. Записати параметричне рівняння прямої. 5. Записати формулу для обчислення довжини відрізка. 6. Записати формулу для обчислення координат середини відрізка. 7. Умова паралельності (перпендикулярності) прямих. Практична робота № 4 Тема: Дослідження форми кривої другого порядку за її канонічним рівнянням. Мета: Навчитися приводити криві другого порядку до канонічного вигляду та досліджувати форму кривої за канонічним рівнянням. Теоретичні відомості:
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.106 (0.007 с.) |

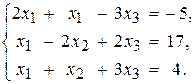

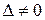 , тому розв’язок можна знайти за формулами Крамера та матричним способом.
, тому розв’язок можна знайти за формулами Крамера та матричним способом. :
:






 :
:
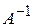 обчислимо алгебраїчні доповнення елементів матриці
обчислимо алгебраїчні доповнення елементів матриці 









 звідки випливає, що
звідки випливає, що  ,
, 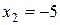 ,
,  .
. В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 

 В=
В= 
 В=
В= 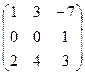
 В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 
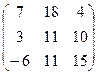 В=
В= 
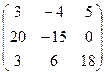 В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 
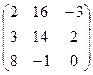 В=
В= 

 В=
В= 
 В=
В= 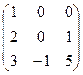
 В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 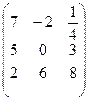
 В=
В= 
 В=
В= 
 В=
В= 
 перпендикулярно до вектора
перпендикулярно до вектора  , який називається нормальним вектором прямої (рис. 2), має рівняння виду:
, який називається нормальним вектором прямої (рис. 2), має рівняння виду:
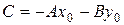 , тоді отримаємо загальне рівняння прямої:
, тоді отримаємо загальне рівняння прямої:
 Пряма, що проходить через точку
Пряма, що проходить через точку 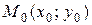 паралельно до вектора
паралельно до вектора  , який називається напрямним вектором прямої (рис. 2), має рівняння виду:
, який називається напрямним вектором прямої (рис. 2), має рівняння виду: (6)
(6) , має рівняння виду:
, має рівняння виду: (7)
(7) знаходять за формулою
знаходять за формулою . (8)
. (8) :
:  ,
,  ,
,  . Знайти:
. Знайти: ,
,  і
і  ;
; і висоти
і висоти  ;
; паралельно прямій
паралельно прямій 
 – напрямний вектор прямої
– напрямний вектор прямої 

 – нормальний вектор прямої
– нормальний вектор прямої 
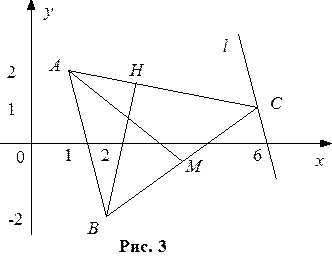 Висота
Висота  (рис. 3), тому нормальний вектор
(рис. 3), тому нормальний вектор  є напрямним для висоти. Скориставшись канонічним рівнянням прямої (6), записуємо рівняння
є напрямним для висоти. Скориставшись канонічним рівнянням прямої (6), записуємо рівняння 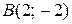


 навпіл сторону
навпіл сторону 
 і
і 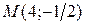 :
:

 , що проходить через точку
, що проходить через точку 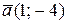 . Запишемо канонічне рівняння прямої
. Запишемо канонічне рівняння прямої 





