
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні правила диференціювання.
Якщо функції 1) 2) 3) При розв’язанні задач на обчислення похідної застосовують ряд формул для похідних основних елементарних функцій: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) Похідна складеної функції. Якщо функція
Похідна функції, заданої параметрично. Похідна функції, яка задана параметрично рівняннями
Диференціювання неявної функції. Нехай рівняння Продиференціювавши обидві частини рівняння Диференціювання показниково-степеневої функції. Похідну показниково-степеневої функції знаходять, провівши попереднє логарифмування.
де
Приклади розв’язання задач Приклад 1. Знайти похідну функції Розв’язання:
Приклад 2. Знайти похідну функції Розв’язання: Приклад 3. Знайти похідну функції, що задана параметрично
Розв’язання:
Приклад 4. Знайти похідну показниково-степеневої функції
Розв’язання:
Приклад 5. Знайти похідну функції, яку задано неявно
Розв’язання:
Похідні вищих порядків. Похідною другого порядку (другою похідною) функції
Приклад 6. Знайти
Розв’язання:
Завдання до виконання
Знайти перші похідні даних функцій. Для б) і д) знайти
Контрольні запитання 1. Таблиця похідних. 2. Правила обчислення похідних. 3. Похідна неявно заданої функції. 4. Похідна показниково- степеневої функції. 5. Похідна функції, заданої параметрично. 6. Похідна складної функції. Практична робота № 6 Тема: Застосування диференціального числення до дослідження функції і побудови графіка. Мета: Навчитись застосовувати набуті теоретичні знання до дослідження функції та побудови графіка. Теоретичні відомості
Література: [5] – с. 449-481, [6] – с. 165-210, [7] – с. 246-266, [8] – с. 167-183. Монотонність функції. Якщо Інтервали монотонності функції (інтервали спадання чи зростання) відділяються один від одного точками, де похідна функції рівна нулю або не існує. Дані точки називаються критичними точками. Щоб знайти інтервали монотонності функції Локальний екстремум. Достатні умови екстремуму: Правило 1. Якщо Правило 2. Якщо
Для знаходження найбільшого (найменшого) значення функції
Приклад 1Знайти найбільше і найменше значення функції Розв’язання: Знайдемо похідну: Знайдемо критичні точки, розв’язавши рівняння Визначимо значення функції в стаціонарних точках і на кінцях відрізка:
Із знайдених значень вибираємо найбільше і найменше:
Опуклість. Увігнутість. Точки перегину. Графік функції Достатні умови опуклості (увігнутості) графіка функції: Якщо Точка Якщо
Приклад 2. Знайти проміжки опуклості та ввігнутості графіка функції Розв’язання: Знайдемо
Асимптоти. Пряма Пряма Пряма Пряма
або
Схема дослідження функції та побудова графіка. 1. Знайти область визначення функції, інтервали неперервності, точки розриву. 2. Знайти (якщо це можливо) точки перетину графіка з координатними осями. 3. Дослідити функцію на періодичність, парність і непарність. 4. Знайти інтервали монотонності, точки локальних екстремумів та значення функції у цих точках. 5. Знайти інтервали опуклості, ввігнутості та перегину. 6. Дослідження функції на межі області існування. Асимптоти графіка. 7. Побудувати графік функції, враховуючи дослідження.
Приклад 3 Дослідити методами диференціального числення функцію
та побудувати її графік Розв’язання: 1. Область визначення: 2. Якщо 3. Функція не періодична. Оскільки 4.
Отже, на У точках 5. Знаходимо
Отже, на
6.
7. Враховуючи проведені дослідження будуємо графік функції.
Завдання до виконання:
Дослідити функції та побудувати їх графіки(Завдання обираються відповідно номера студента в друкованому списку журналу):
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
27.
28. Контрольні запитання: 1. Що таке область допустимих значень функції? 2. Надати класифікацію точок розриву. 3. В яких точках можуть існувати вертикальні асимптоти? 4. Як знайти похилі асимптоти? 5. Дати означення парної (непарної) функції 6. Дати означення періодичної функції. Навести приклади періодичних функцій. 7. Дати означення критичних точок першого та другого роду. 8. Як знайти проміжки монотонності та екстремуми функції? 9. Як знайти проміжки опуклості та угнутості функції та точки перегину? 10. Як знайти точки перетину графіка функції з осями координат? Практична робота № 7 Тема: Інтегрування раціональних функцій. Мета: Навчитися інтегрувати раціональні функції. Вміти користуватися методом невизначених коефіцієнтів. Теоретичні положення: Інтегрування раціональних дробів дробів. Раціональним дробом називається вираз Найпростіші (елементарні) дроби: 1) 2) 3) 4) Інтеграли від елементарних дробів 1-2 типу: 1) 2) 3) Щоб обчислити інтеграл 3-го типу необхідно: а) виділити в чисельнику похідну знаменника; б) розбити інтеграл на два; в) у другому інтегралі виділити у знаменнику повний квадрат.
Приклад 1. Знайти невизначений інтеграл Розв’язання:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.170.17 (1.914 с.) |
 і
і 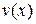 диференційовні в точці
диференційовні в точці  , тоді в цій точці мають місце такі співвідношення:
, тоді в цій точці мають місце такі співвідношення: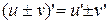 ;
; ;
; .
. ;
; , (
, (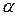 – довільне число);
– довільне число); , (
, ( );
);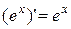 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; ;
; ;
;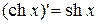 ;
; ;
; .
. має похідну
має похідну  в точці
в точці  має похідну
має похідну  у відповідній точці
у відповідній точці  , то складена функція
, то складена функція  має похідну
має похідну  в точці
в точці  .
. , де
, де  і
і 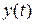 диференційовні в точці
диференційовні в точці  , причому
, причому 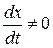 , обчислюється за формулою:
, обчислюється за формулою: .
. визначає
визначає 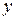 як неявну функцію від
як неявну функцію від 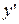 . З цього рівняння легко знайти
. З цього рівняння легко знайти 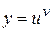 – показниково-степенева функція,
– показниково-степенева функція, – задані і диференційовні функції від
– задані і диференційовні функції від  ,
,  ,
, 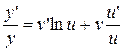 ;
;  .
. .
.

 .
.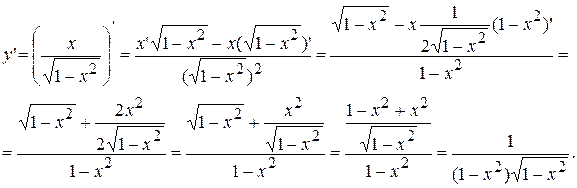

 . Знайдемо
. Знайдемо  і
і  .
.


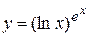 .
. ,
,  ,
, ,
,  ,
,  .
. .
. ,
,  ,
,  ,
, ,
,  ,
,  .
. називається похідна від її похідної. Друга похідна позначається так:
називається похідна від її похідної. Друга похідна позначається так: 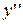 або
або  , або
, або 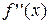 . Аналогічно похідною третього порядку функції
. Аналогічно похідною третього порядку функції  . Взагалі, похідною
. Взагалі, похідною  -го порядку від функції
-го порядку від функції  -го порядку:
-го порядку:  . Позначають
. Позначають  або
або  , або
, або 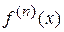 . Якщо функція задана параметрично:
. Якщо функція задана параметрично: 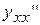 обчислюється за формулою:
обчислюється за формулою:  .
.

 .
. .
. ;
;
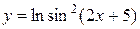 ;
;
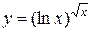 ;
;
 ;
;
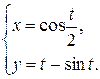
 ;
;
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;
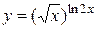 ;
;
 ;
;
 ,
,  .
.
 ;
;
 ;
;
 ;
;
 ;
;

 ;
;
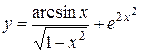 ;
;
 ;
;
 ;
;

 .
.
 ;
;
 ;
;
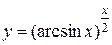 ;
;
 ;
;

 ;
;
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;
 ;
;
 ;
;

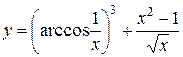 ;
;
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;
 ;
;
 ;
;

 .
.
 і
і  всюди, крім, можливо, скінченого числа точок, в яких
всюди, крім, можливо, скінченого числа точок, в яких  на
на  не існує; 4) розділити критичними точками область визначення на інтервали і в кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від’ємна – спадає.
не існує; 4) розділити критичними точками область визначення на інтервали і в кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від’ємна – спадає. – критична точка функції
– критична точка функції 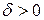 виконуються нерівності
виконуються нерівності  , то функція
, то функція  ,то
,то  і
і  однакові, то функція
однакові, то функція  екстремуму не має.
екстремуму не має.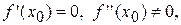 то функція
то функція  , і мінімум, якщо
, і мінімум, якщо  .
. необхідно із значень функції на кінцях відрізка і в критичних точках, які належать даному відрізку, вибрати найбільше (найменше).
необхідно із значень функції на кінцях відрізка і в критичних точках, які належать даному відрізку, вибрати найбільше (найменше). на відрізку
на відрізку  .
.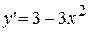 .
. – стаціонарні точки, які належать вказаному відрізку
– стаціонарні точки, які належать вказаному відрізку  .
. на
на 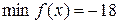 на
на  графіка функції, яка відділяє його опуклу частину від увігнутої називається точкою перегину. В абсцисах точок перегину друга похідна функції дорівнює нулю або не існує (
графіка функції, яка відділяє його опуклу частину від увігнутої називається точкою перегину. В абсцисах точок перегину друга похідна функції дорівнює нулю або не існує ( або
або  – не існує). Точки, в яких
– не існує). Точки, в яких 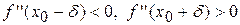 або
або  , то точка кривої
, то точка кривої  .
. .
.  – критична точка другого роду. Якщо
– критична точка другого роду. Якщо 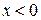 , то
, то  – крива опукла. Якщо
– крива опукла. Якщо  , то
, то  – крива ввігнута. Отже, на проміжку
– крива ввігнута. Отже, на проміжку  – крива випукла, а на
– крива випукла, а на  – ввігнута.
– ввігнута. називається асимптотою кривої
називається асимптотою кривої  кривої до прямої
кривої до прямої  є вертикальною асимптотою кривої
є вертикальною асимптотою кривої  .
. є горизонтальною асимптотою кривої
є горизонтальною асимптотою кривої  або
або  .
. є похилою асимптотою кривої
є похилою асимптотою кривої 


 . Точки розриву
. Точки розриву  .
. , тому графік перетинає осі координат в точці
, тому графік перетинає осі координат в точці  .
. , то функція непарна, а отже графік функції симетричний відносно початку координат.
, то функція непарна, а отже графік функції симетричний відносно початку координат. . Розв’язком даного рівняння є
. Розв’язком даного рівняння є  . Похідна не існує в
. Похідна не існує в  . Знайдемо знаки
. Знайдемо знаки 
 – функція спадає,
– функція спадає,  – функція зростає,
– функція зростає,  – функція спадає.
– функція спадає. функція має локальний екстремум:
функція має локальний екстремум:  – локальний максимум,
– локальний максимум,  – локальний мінімум.
– локальний мінімум. . Похідна
. Похідна  при
при 
 – крива ввігнута, на
– крива ввігнута, на  – крива опукла.
– крива опукла. – похила асимптота.
– похила асимптота.
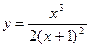 14.
14. 
 15.
15. 
 16.
16. 
 17.
17. 
 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 29.
29. 
 30.
30. 
 , де
, де  і
і 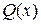 – многочлени. Раціональний дріб називається правильним, якщо степінь многочлена
– многочлени. Раціональний дріб називається правильним, якщо степінь многочлена  ;
;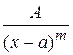 , де
, де  ;
; , де
, де 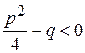 , тобто квадратний тричлен
, тобто квадратний тричлен  не має дійсних коренів;
не має дійсних коренів;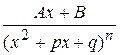 , де
, де  ,
,  ;
; ;
; .
.



