
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило обчислення визначника n-го порядку.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Визначник n порядку дорівнює сумі добутків усіх елементів будь-якого стовпця (або рядка) на відповідні їм алгебраїчні доповнення. У випадку використання і-го рядка це правило математично виглядає так
Рівність (4) називають розкладом визначника за елементами і-го рядка. Зауваження. Обчислення визначника n порядку зводиться до обчислення n визначників (n-1) порядку. Для скорочення обчислень визначник доцільно розкладати за елементами рядка або стовпця, який містить найбільшу кількість нулів. До нулів не треба знаходити алгебраїчних доповнень тому, що добуток 0 на його алгебраїчне доповнення дорівнює нулю. Властивості визначника дозволяють робити еквівалентні перетворення визначника і одержувати якомога більше нулів в деякому рядку або стовпці.
Властивості визначників. 1 Визначник при транспонуванні не змінюється: |А|=|Ат|. Наслідок. Рядки та стовпці визначника мають однакові властивості.
2 Якщо у визначнику поміняти місцями будь-які два рядки (стовпці), то визначник змінить знак на протилежний. 3 Якщо визначник має два однаковихрядка (стовпця), то він дорівнює 0. 4 Якщо усі елементи одного рядка (стовпця) визначника помножити на однакове число к, то визначник зросте в к разів. Наслідок 1. Спільний множник усіх елементів будь-якого рядка (стовпця) визначника можна виносити за знак визначника. Наслідок 2. Якщо усі елементи будь-якого рядка (стовпця) визначника дорівнюють нулю, то визначник дорівнює нулю.
5 Якщо елементи двох будь-яких рядків (стовпців) визначника пропорційні, то визначник дорівнює нулю. 6 Якщо до всіх елементів будь-якого рядка (стовпця) визначника додати відповідні елементи іншого рядка (стовпця) цього визначника, помножені на однакове число, то визначник не зміниться. Приклад 5. Обчислити визначник 4-го порядку.
Розв’язання. Якщо цей визначник обчислювати шляхом його розкладу за елементами 1-го стовпця або 2-го рядка (вони містять один нуль), то треба буде знайти та обчислити три алгебраїчних доповнення – визначники третього порядку. Перетворимо цей визначник так, щоб одержати якомога більше нулів у другому рядку, бо там вже є один нуль і є одиниця, яка спрощує перетворення. Елементи другого стовпця помножимо на (-2) і додамо до відповідних елементів третього стовпця, потім елементи другого стовпця помножимо на 4 і додамо до відповідних елементів четвертого стовпця. Одержимо визначник
Тепер визначник доцільно розкласти за елементами другого рядка
Останню рівність одержали шляхом виносу за знак визначника загального множника (-3) елементів другого стовпця. Використовуючи правило обчислення визначника третього порядку, одержимо |А| = -3 (7 + 130 - 33 - 55 + 42 - 13) = -3(179 - 101 ) = (-3)∙78 = -234
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ.
Обчисліть визначники: 1. а)
б)
в)
2.
Розв’язання. Перший спосіб. За правилом трикутників маємо
Другий спосіб. Використовуючи властивості визначника, дістаємо
=
Третій спосіб. Розкладемо визначник за першим рядком:
3.
Розв’язання. У визначнику є кілька нульових елементів, проте зручно, коли нульові елементи містяться в одному рядку чи стовпцеві. Зробимо, наприклад, нульовими всі елементи першого рядка, крім першого елемента. Для цього додамо до третього стовпця перший, після чого помножимо елементи першого стовпця на -2 і додамо їх до відповідних елементів четвертого стовпця. Дістанемо
Тепер розкладемо визначник за елементами першого рядка:
Занулимо два елементи другого стовпця. Для цього до першого і другого рядків по черзі додамо третій рядок. Тоді
Розкладемо утворений визначник за елементами другого стовпця:
Відповідь: 4. Розв’яжіть рівняння:
Розв’язання. Розкладемо визначник за елементами першого рядка:
Отже, вихідне рівняння рівносильне рівнянню
Далі маємо
Відповідь:
ВПРАВИ ДЛЯ АУДИТОРНОЇ РОБОТИ.
Обчисліть визначники: 1.
5.
9. 12.
13. Доведіть рівність:
Відповіді: 1. 66. 2. -110. 3. 121. 4. 1. 5. 5/3. 6. 0,6. 7. 13/21. 8. -5. 9. -10. 10. -15. 11. 11. 12. 12.
САМОСТІЙНА РОБОТА №2 2.1. Обчисліть визначники, використовуючи: а) метод зведення до трикутного вигляду; б) метод розкладу визначника за елементами деякого рядка або стовпця; в) правило трикутників.
1)
5)
9)
13)
17)
21)
25)
2.2. Знайдіть дійсні корені рівняння:
1)
3)
5)
7)
9)
11)
13)
15)
17)
19)
21)
23)
25)
2.3. Обчисліть визначники четвертого порядку, комбінуючи метод зведення до трикутного вигляду та метод розкладу визначника за елементами деякого рядка (стовпця). 1)
4)
7)
10)
13)
16)
19)
22)
25)
---------------------------------------------------------------------------------------------------- САМОСТІЙНА РОБОТА №3 Тема 3. Ранг матриці.
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.178.162 (0.006 с.) |





 ;
; ;
; .
.


 =
=  =
=  =
= .
. +
+  +
+  =
=  .
.
 =
=  =
=  .
. .
. .
. .
. .
. .
.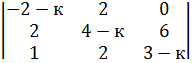 =
= 
 =
=  =
=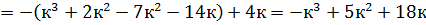 .
.
 ;
;  або
або  , звідси
, звідси  .
. ;
;  .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
. . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  .
. . 10.
. 10.  . 11.
. 11.  .
. .
. =авс(в-а)(с-а)(с-в).
=авс(в-а)(с-а)(с-в). . 2)
. 2)  . 3)
. 3)  . 4)
. 4)  .
. . 6)
. 6)  . 7)
. 7)  . 8)
. 8)  .
.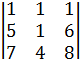 . 10)
. 10)  . 11)
. 11)  . 12)
. 12) 
 . 14)
. 14)  . 15)
. 15)  . 16)
. 16)  .
. . 18)
. 18)  . 19)
. 19)  . 20)
. 20) 
 . 22)
. 22)  . 23)
. 23)  . 24)
. 24)  .
. .
. . 2)
. 2)  .
. . 4)
. 4)  .
. . 6)
. 6)  .
. . 8)
. 8)  .
. . 10)
. 10) 
 . 12)
. 12)  .
. . 14)
. 14)  .
. . 16)
. 16)  .
. .
. . 20)
. 20)  .
.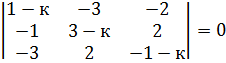 . 22)
. 22)  .
. . 24)
. 24)  .
. .
. . 2)
. 2)  . 3)
. 3)  .
. . 5)
. 5)  . 6)
. 6)  .
. . 8)
. 8)  . 9)
. 9)  .
. . 11)
. 11)  . 12)
. 12)  .
. . 14)
. 14)  . 15)
. 15) 
 .17)
.17)  .18)
.18) 
 . 20)
. 20)  . 21)
. 21)  .
. . 23)
. 23)  . 24)
. 24)  .
. .
.


