
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вправи для аудиторної роботи.Содержание книги Поиск на нашем сайте
1. Вектори
2. Дано вектори а) скалярний добуток б) кут між векторами в) проекцію вектора
3. Дано вектори
САМОСТІЙНА РОБОТА №9
9.1. Дано точки а) координати, довжину, напрямні косинуси та орт вектора б) координати точки М, якщо в) координати точки
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25)
9.2. Чи колінеарні вектори 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25)
9.3. Обчисліть: 1) а) 2) а) 3) а) 4) а) 5) а) 6) а) 7) а) 8) а) 9) а) 10) а) 11) а) 12) а) 13) а) 14) а) 15) а) 16) а) 17) а) 18) а) 19) а) 20) а) 21) а) 22) а) 23) а) 24) а) 25) а)
9.4. Знайдіть скалярний добуток 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25)
9.5. Знайдіть вектор 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) ---------------------------------------------------------------------------------------------------
Тема 4. Векторний добуток векторів.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
Векторним добутком вектора 1) модуль вектора
де 2) вектор 3) вектори
Рис.1
Позначення векторного добутку: З означення векторного добутку безпосередньо випливають векторні рівності між ортами
Властивості векторного добутку.
Розглянемо алгебраїчні та геометричні властивості векторного добутку: 1) геометричний зміст векторного добутку: модуль векторного добутку дорівнює площі паралелограма, побудованого на прикладених до спільного початку векторах
2) антикомутативність множення:
3) 4) 5) два ненульові вектори
Зокрема,
Зауваження. Якщо відомі координати вершин трикутника АВС, то його площу доцільно шукати за формулою
Векторний добуток векторів, заданих координатами.
Нехай вектори
або
Мішаний добуток векторів.
Мішаним (векторно-скалярним) добутком трьох векторів
Розглянемо властивості мішаного добутку. 1. Якщо в мішаному добутку поміняти місцями які-небудь два множники, то мішаний добуток змінить знак, наприклад:
2. При циклічному переставленні множників мішаний добуток не змінюється. 3. У мішаному добутку знаки векторного і скалярного добутків можна міняти місцями:
4. Геометричний зміст мішаного добутку: модуль мішаного добутку
Рис.3
Зауваження. Об’єм піраміди, побудованої на векторах
5. Якщо 6. Умова компланарності трьох векторів.
Мішаний добуток трьох векторів, заданих координатами.
Нехай вектори
Дістали розклад визначника третього порядку за елементами першого рядка. Отже,
Зауваження. Компланарність ненульових векторів
то вектори
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.80 (0.01 с.) |

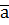 і
і  утворюють кут
утворюють кут  . Знаючи, що
. Знаючи, що 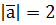 ,
, 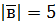 , обчисліть: а)
, обчисліть: а) 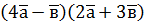 ; б)
; б) 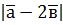 .
. і
і  . Знайдіть:
. Знайдіть: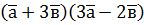 ;
; та
та  ;
;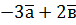 на вектор
на вектор 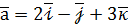 ,
, 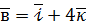 ,
, 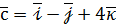 . Знайдіть вектор
. Знайдіть вектор  , який задовольняє рівності:
, який задовольняє рівності:  ,
, 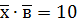 та
та 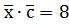 .
.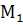 та
та 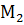 . Знайдіть:
. Знайдіть: ;
;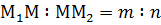 ;
;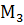 , якщо
, якщо 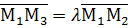
 ,
, 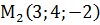 ,
, 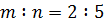 ,
, 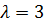 .
.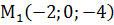 ,
, 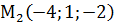 ,
, 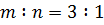 ,
, 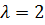 .
. ,
,  ,
, 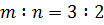 ,
, 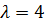 .
.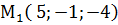 ,
, 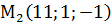 ,
,  ,
, 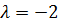 .
.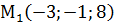 ,
, 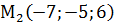 ,
, 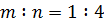 ,
,  .
.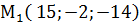 ,
,  ,
, 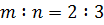 ,
, 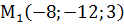 ,
,  ,
, 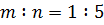 ,
,  ,
, 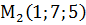 ,
, 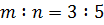 ,
, 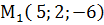 ,
, 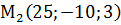 ,
, 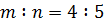 ,
,  ,
,  ,
, 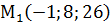 ,
, 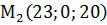 ,
, 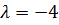 .
.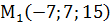 ,
,  ,
, 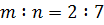 ,
, 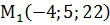 ,
, 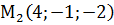 ,
, 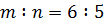 ,
, 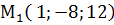 ,
, 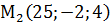 ,
, 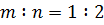 ,
, 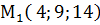 ,
, 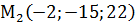 ,
, 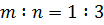 ,
,  ,
, 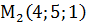 ,
,  ,
, 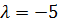 .
.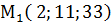 ,
,  ,
,  ,
,  ,
,  ,
, 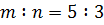 ,
, 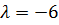 .
. ,
,  ,
,  ,
, 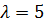 .
. ,
, 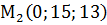 ,
, 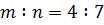 ,
,  .
. ,
, 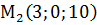 ,
, 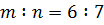 ,
, 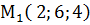 ,
, 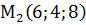 ,
,  ,
, 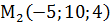 ,
, 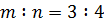 ,
,  ,
, 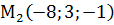 ,
, 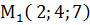 ,
, 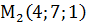 ,
,  і
і  , побудовані на векторах
, побудовані на векторах  ,
,  ,
, 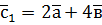 ,
, 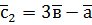 .
. ,
, 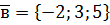 ,
,  ,
,  .
. ,
, 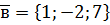 ,
, 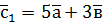 ,
,  .
.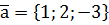 ,
, 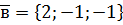 ,
,  ,
,  .
. ,
, 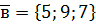 ,
, 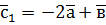 ,
, 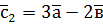 .
.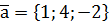 ,
, 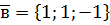 ,
,  ,
, 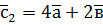 .
. ,
, 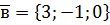 ,
, 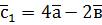 ,
, 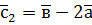 .
. ,
,  ,
, 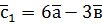 ,
, 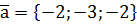 ,
, 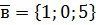 ,
,  ,
, 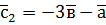 .
. ,
,  ,
, 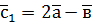 ,
, 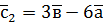 .
.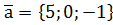 ,
,  ,
,  .
. ,
, 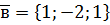 ,
,  ,
, 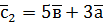 .
.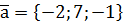 ,
, 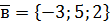 ,
, 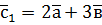 ,
,  .
. ,
, 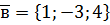 ,
,  .
.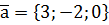 ,
,  ,
, 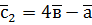 .
. ,
, 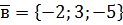 ,
,  ,
,  .
.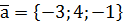 ,
, 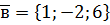 ,
, 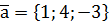 ,
, 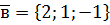 ,
, 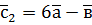 .
.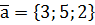 ,
, 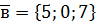 ,
, 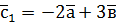 ,
,  ,
, 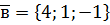 ,
,  .
. ,
, 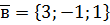 ,
,  ,
, 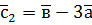 .
.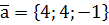 ,
, 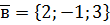 ,
, 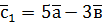 ,
, 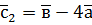 .
.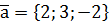 ,
, 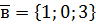 ,
, 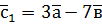 ,
,  .
.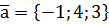 ,
, 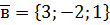 ,
, 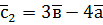 .
.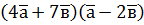 ; б)
; б) 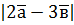 , якщо
, якщо 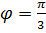 .
.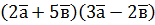 ; б)
; б)  , якщо
, якщо  ,
, 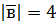 ,
,  .
.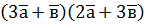 ; б)
; б)  ,
, 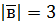 ,
,  .
.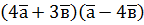 ; б)
; б)  , якщо
, якщо  ,
, 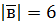 ,
, 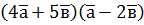 ; б)
; б) 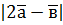 , якщо
, якщо 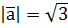 ,
, 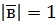 ,
,  .
.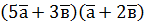 ; б)
; б) 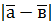 , якщо
, якщо 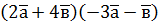 ; б)
; б) 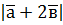 , якщо
, якщо  ,
, 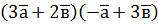 ; б)
; б) 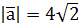 ,
, 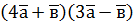 ; б)
; б) 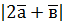 , якщо
, якщо 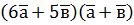 ; б)
; б)  , якщо
, якщо 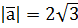 ,
,  ; б)
; б)  , якщо
, якщо 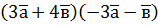 ; б)
; б) 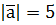 ,
,  ; б)
; б)  , якщо
, якщо 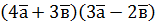 ; б)
; б) 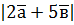 , якщо
, якщо 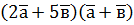 ; б)
; б)  .
.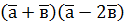 ; б)
; б) 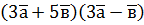 ; б)
; б) 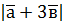 , якщо
, якщо  ,
, 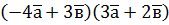 ; б)
; б) 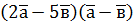 ; б)
; б)  ,
,  ; б)
; б) 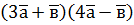 ; б)
; б) 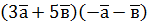 ; б)
; б) 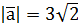 ,
,  ; б)
; б)  ; б)
; б)  ,
,  , кут між векторами
, кут між векторами  і
і 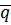 та проекцію вектора
та проекцію вектора  ,
,  ,
, 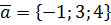 ,
, 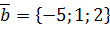 .
. ,
, 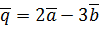 ,
, 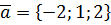 ,
, 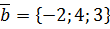 .
.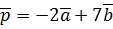 ,
,  ,
,  ,
, 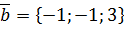 .
. ,
, 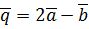 ,
, 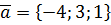 ,
,  .
. ,
,  ,
,  .
.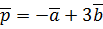 ,
,  ,
, 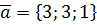 ,
, 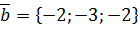 .
.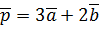 ,
,  ,
, 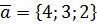 ,
, 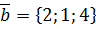 .
. ,
,  ,
,  .
. ,
,  ,
, 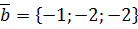 .
. ,
, 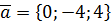 ,
,  .
.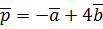 ,
,  ,
,  ,
, 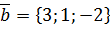 .
. ,
,  ,
,  .
. ,
, 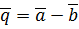 ,
,  ,
, 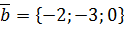 .
.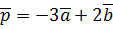 ,
, 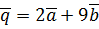 ,
, 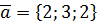 ,
, 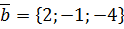 .
.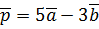 ,
, 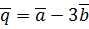 ,
, 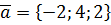 ,
,  .
. ,
, 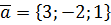 ,
, 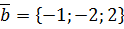 .
.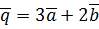 ,
,  ,
, 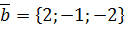 .
.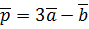 ,
,  ,
,  ,
, 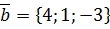 .
.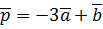 ,
,  ,
, 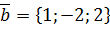 .
.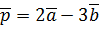 ,
, 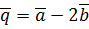 ,
,  ,
, 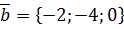 .
.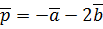 ,
, 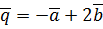 ,
, 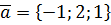 ,
, 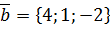 .
.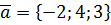 ,
,  .
.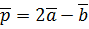 ,
, 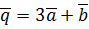 ,
,  ,
, 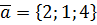 ,
,  .
. ,
, 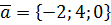 ,
, 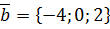 .
.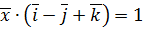 ,
,  ,
, 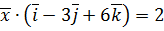 .
.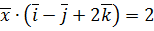 ,
, 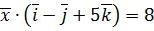 ,
, 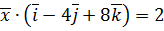 .
.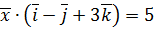 ,
, 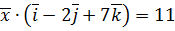 ,
, 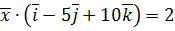 .
.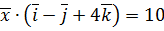 ,
, 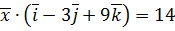 ,
, 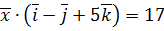 ,
, 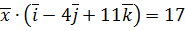 ,
, 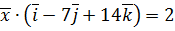 .
. ,
, 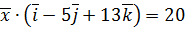 ,
, 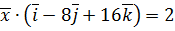 .
. ,
, 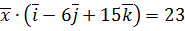 ,
, 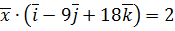 .
.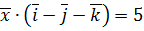 ,
,  ,
, 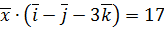 ,
, 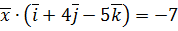 ,
,  .
.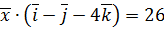 ,
, 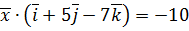 ,
, 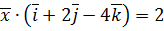 .
. ,
,  ,
,  .
. ,
,  ,
, 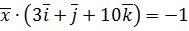 .
. ,
, 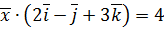 ,
,  .
.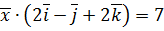 ,
,  ,
, 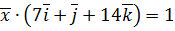 .
.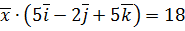 ,
, 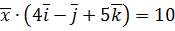 ,
,  .
. ,
, 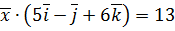 ,
, 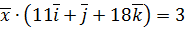 .
. ,
, 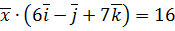 ,
, 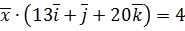 .
. ,
, 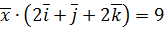 ,
,  .
.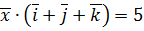 ,
, 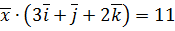 ,
,  .
.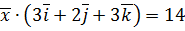 ,
,  ,
,  .
.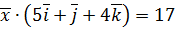 ,
, 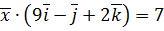 .
.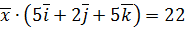 ,
, 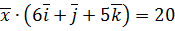 ,
, 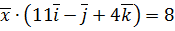 .
. ,
,  ,
, 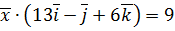 .
. ,
, 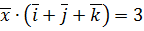 ,
,  .
.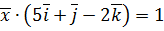 ,
,  ,
, 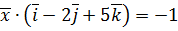 .
. на вектор
на вектор  називають вектор
називають вектор  , який задовольняє такі три умови:
, який задовольняє такі три умови: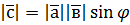 ,
, - кут між векторами
- кут між векторами  ,
, 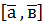 .
.
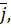
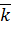 :
:

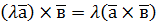 ;
;  ;
; ;
; колінеарні тоді і тільки тоді, коли векторний добуток цих векторів дорівнює нуль-вектору, тобто
колінеарні тоді і тільки тоді, коли векторний добуток цих векторів дорівнює нуль-вектору, тобто

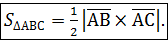
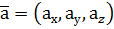 ,
,  задані своїми координатами у ПДСК. Тоді векторний добуток знаходять за формулою
задані своїми координатами у ПДСК. Тоді векторний добуток знаходять за формулою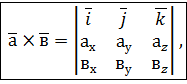

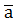 ,
,  називають число
називають число 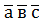 , рівне скалярному добутку вектора
, рівне скалярному добутку вектора 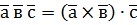
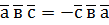 .
.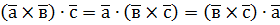 .
.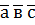 чисельно дорівнює об’єму паралелепіпеда, побудованого на прикладених до спільного початку векторах
чисельно дорівнює об’єму паралелепіпеда, побудованого на прикладених до спільного початку векторах 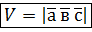

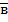 S
S
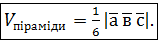
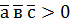 , то вектори
, то вектори  , то ліву трійку.
, то ліву трійку.
 ,
, 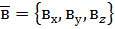 ,
, 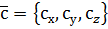 задані своїми координатами в ПДСК. Знайдемо мішаний добуток цих векторів, використовуючи формули скалярного і векторного добутку векторів, заданих координатами. Маємо
задані своїми координатами в ПДСК. Знайдемо мішаний добуток цих векторів, використовуючи формули скалярного і векторного добутку векторів, заданих координатами. Маємо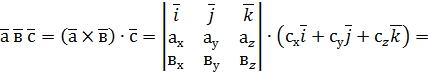
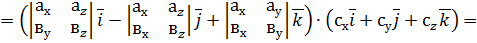
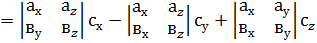 .
.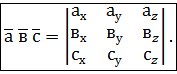
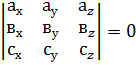 ,
,


