
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поділ відрізка у даному відношенні.Содержание книги Поиск на нашем сайте
Нехай задано відрізок
Зокрема, координати точки, яка ділить відрізок навпіл (
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ.
1. Дано точки а) координати, довжину, напрямні косинуси та орт вектора б) координати точки М, яка ділить відрізок Розв'язання. а)
Орт вектора
б)
2. Знайдіть вектор Розв'язання. Враховуючи рівності
і умову
звідки дістаємо Відповідь:
3. Чи колінеарні вектори
Розв'язання. Послідовно дістаємо
Оскільки координати векторів 4. Початком вектора Розв'язання. Враховуючи умову рівності двох векторів, дістанемо
або
звідси
5. Відомо, що вектори Розв'язання. Записуємо умову колінеарності заданих векторів:
звідси
6. Знайдіть подання вектора
Розв'язання. Передусім переконуємось, що вектори
або Звідси дістаємо систему рівнянь
розв’язок якої
Отже,
ВПРАВИ ДЛЯ АУДИТОРНОЇ РОБОТИ.
1. Дано точки а) координати, довжину, напрямні косинуси та орт вектора б) координати точки М, яка ділить відрізок 2. Знайдіть вектор 3. Чи колінеарні вектори
4. Відомо, що вектори 5. Знайдіть подання вектора
---------------------------------------------------------------------------------------------------- Тема 3. Скалярний добуток векторів.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Скалярним добутком двох векторів
Якщо хоча б один із векторів
Оскільки виконуються рівності
то
Геометричний зміст скалярного добутку: скалярний добуток двох векторів дорівнює добутку довжини одного вектора на проекцію на нього другого вектора (рис.1).
Тоді
Формула (1) – робоча формула для обчислення проекції вектора на вектор (або вісь).
Властивості скалярного добутку.
Алгебраїчні властивості скалярного добутку: 1. 2. 3.
Геометричні властивості скалярного добутку: 1. якщо 2. скалярний добуток двох ненульових векторів дорівнює нулю тоді і тільки тоді, коли ці вектори перпендикулярні; 3. скалярний квадрат вектора дорівнює квадрату його довжини, тобто
звідки
Умова перпендикулярності двох векторів.
Ненульові вектори
Зокрема:
Вираз скалярного добутку через координати. Кут між векторами.
Нехай вектори
Тоді
Висновки з формули (3) такі: 1. умова перпендикулярності векторів
2. довжина вектора
3. косинус кута між векторами
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ.
1. Вектори Розв'язання. а)
Оскільки правильні рівності
то
б) скориставшись формулою (2), дістанемо
2. Дано вектори а) скалярний добуток Розв'язання. а)
б)
звідси
3. Дано вектори Розв'язання. Нехай
дістанемо значення: Відповідь:
4. Точки Розв'язання. Знайдемо координати векторів
Косинус кута
звідки Проекцію вектора
5. Нехай точки
Розв'язання. Утворимо вектори:
Діагоналі чотирикутника будуть взаємно перпендикулярні тоді, коли скалярний добуток
звідки дістанемо а=1,5.
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 971; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.29.0 (0.01 с.) |

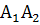 точками
точками 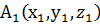 і
і 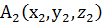 . Тоді координати точки М(х, у, z), яка ділить цей відрізок у відношенні
. Тоді координати точки М(х, у, z), яка ділить цей відрізок у відношенні  , тобто
, тобто  , знаходять за формулами
, знаходять за формулами (4)
(4) , такі:
, такі:
 ,
,  . Знайдіть:
. Знайдіть: ;
;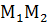 у відношенні
у відношенні 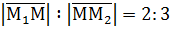 .
.
 ;
;  ,
, 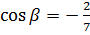 ,
, 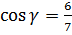 .
.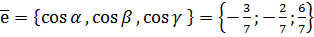 .
. , тоді
, тоді ,
, 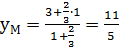 ,
,  .
. , якщо він утворює з осями координат однакові кути і
, якщо він утворює з осями координат однакові кути і 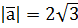 .
. ,
,  ,
, 
 , записуємо співвідношення
, записуємо співвідношення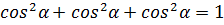 ,
,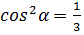 ,
,  ,
, 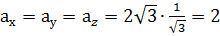 або
або  .
.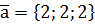 або
або  .
. і
і  побудовані на векторах
побудовані на векторах і
і  ?
?
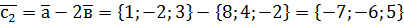 .
.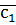 і
і  не пропорційні, то ці вектори не колінеарні.
не пропорційні, то ці вектори не колінеарні. є точка
є точка  . Знайдіть координати точки Р, яка є кінцем вектора
. Знайдіть координати точки Р, яка є кінцем вектора 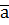 .
. ,
,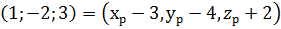
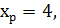
 ,
,  , тобто
, тобто 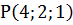 - кінець вектора
- кінець вектора  та
та 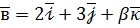 колінеарні. Знайдіть
колінеарні. Знайдіть  і
і 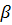 .
.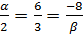
 ,
, 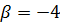 .
.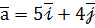 у базисі
у базисі  ,
,  .
.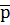 і
і 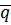 утворюють базис:
утворюють базис: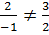 . Записуємо розклад
. Записуємо розклад  , де коефіцієнти
, де коефіцієнти 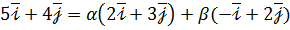

 ,
, ,
, 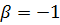 .
. .
.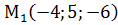 ,
,  . Знайдіть:
. Знайдіть: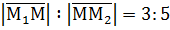 .
.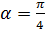 та
та 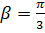 відповідно, і
відповідно, і 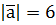 .
. і
і  побудовані на векторах
побудовані на векторах і
і 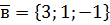 ?
? та
та  колінеарні. Знайдіть
колінеарні. Знайдіть  у базисі
у базисі 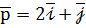 ,
,  .
. і
і  називають число
називають число 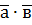 , що дорівнює добутку довжин цих векторів на косинус кута між ними:
, що дорівнює добутку довжин цих векторів на косинус кута між ними:
 нульовий, то за означенням
нульовий, то за означенням .
. ,
, 
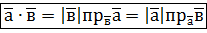

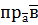
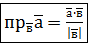 (1)
(1) ;
;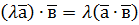 ;
;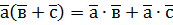 .
. та
та  , то
, то  , якщо кут
, якщо кут  , якщо кут
, якщо кут  ,
, . (2)
. (2)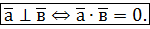
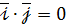 ,
,  ,
, 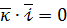
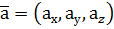 ,
,  .
. (3)
(3) ;
; ;
; .
.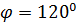 . Знаючи, що
. Знаючи, що  ,
, 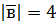 , обчисліть: а)
, обчисліть: а) 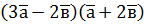 ; б)
; б) 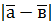 .
.
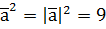 ,
,  ,
, 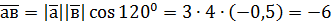
 ;
;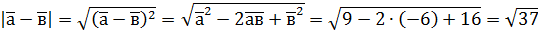 .
. і
і  . Знайдіть:
. Знайдіть: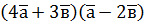 ; б) кут між векторами
; б) кут між векторами  та
та  .
.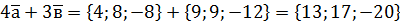 ,
,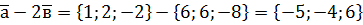 ,
, ;
; ,
,  ,
, ,
, .
. ,
, 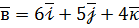 ,
, 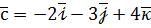 . Знайдіть вектор
. Знайдіть вектор  , який задовольняє рівності:
, який задовольняє рівності:  ,
,  та
та 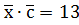 .
.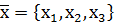 , тоді умова
, тоді умова  . Аналогічно дістаємо ще два рівняння
. Аналогічно дістаємо ще два рівняння та
та 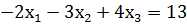 . Розв’язавши систему
. Розв’язавши систему
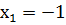 ,
,  ,
,  .
. .
. ,
,  ,
,  - вершини трикутника АВС. Знайдіть кут у трикутнику при вершині В і проекцію вектора
- вершини трикутника АВС. Знайдіть кут у трикутнику при вершині В і проекцію вектора  на вектор
на вектор 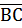 .
.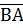 і
і  ,
, 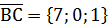 .
.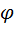 між векторами
між векторами  ,
, . Отже,
. Отже, 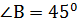 .
. .
.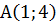 ,
, 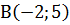 ,
,  ,
, 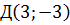 - послідовні вершини чотирикутника АВСД. При якому значенні а діагоналі чотирикутника взаємно перпендикулярні?
- послідовні вершини чотирикутника АВСД. При якому значенні а діагоналі чотирикутника взаємно перпендикулярні? ,
, 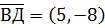 .
.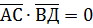 , тобто
, тобто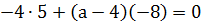 ,
,


