
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К. Г. Валуєв, І. А. Джаладова «Вища математика. Навчальний посібник» - К. - 2003Содержание книги
Поиск на нашем сайте
Тема 1. Матриці та дії над ними.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Означення 1 .Матрицею розміром m x n називають таблицю упорядкованих чисел або будь-яких інших об'єктів, розташованих в m рядках та n стовпцях. Матриці позначають великими літерами, наприклад, А, В,С, та круглими дужками, а елементи матриць позначають відповідними малими літерами з двома індексами, наприклад, аij, вij, сij. Перший індекс і вказує номер рядка, в якому знаходиться цей елемент, другий індекс j вказує номер стовпця, який містить цей елемент. Так, елемент С43 знаходиться на перетині четвертого рядка та третього стовпця матриці С. Матриця розміру пх1 називається матрицею-стовпцем або вектором-стовпцем. Матриця розміру 1хп називається матрицею-рядком або вектором-рядком. Матрицю називають квадратною порядку п, якщо кількість її рядків однакова з кількістю стовпців і дорівнює п.
Приклад 1. Нехай задані матриці
Матриця А має розмір 3x4, матриця В розміру 2x3, матриця-стовпець С розміру 4x1, D - матриця рядок розміру 1x4, матриця К - квадратна порядку 3. Елементи квадратної матриці А порядку n, що розташовані на діагоналі матриці, яка проходить з лівого верхнього кута до правого нижнього кута, утворюють головну діагональ матриці. Елементи квадратної матриці, що розташовані на діагоналі матриці, яка проходить з правого верхнього кута до лівого нижнього кута, утворюють неголовну (побічну) діагональ матриці.
Наприклад, в матриці
елементами головної діагоналі будуть: a11, a22, a33,..., ann, a елементами неголовної діагоналі будуть: а1n, а2(n-1), а3(n-2),..., an1. Квадратна матриця зветься діагональною, якщо усі її елементи дорівнюють 0, крім елементів головної діагоналі. Діагональна матриця, усі елементи якої дорівнюють одиниці, називається одиничною матрицею і позначається Е або І.
Наприклад,
Матриці А та В називають рівними, якщо: 1. вони мають однаковий розмір; 2. їх відповідні елементи рівні, тобто aij= вij для усіх і та j. Якщо в матриці А рядки записати стовпцями із збереженням їх нумерації, то одержана матриця зветься транспонованою і позначається АT, а вказана операція перетворення матриці А називається транспонуванням матриці А.
Наприклад, якщо Матриці широко використовуються не лише в різних навчальних дисциплінах, але й в практичній діяльності спеціалістів багатьох галузей, тому треба розуміти правила дій з матрицями і мати навички їх використання.
Найпростіші дії з матрицями
Найпростішими діями з матрицями називають множення матриць на число, їх алгебраїчну суму та множення матриць. Добутком матриці А на число к називається матриця, елементи якої дорівнюють добуткам відповідних елементів матриці А та числа к:
(1) Додавати та віднімати можна лише матриці однакового розміру!!! Алгебраїчною сумою матриць А та В однакового розміру m x n називається матриця С розміру m x n, елементи якої дорівнюють такої самої алгебраїчної суми елементів aij та вij матриць А та В:
Наприклад, якщо
Добуток А Добутком А
Зауваження 1. Взагалі добуток матриць не має властивості комутативності, тобто АВ≠ВА. Якщо добуток двох матриць не залежить від порядку множників, тобто АВ = ВА, тоді кажуть, що ці матриці комутують. Наприклад, якщо А - квадратна матриця порядку n, Е - одинична матриця порядку n, тоді АЕ = ЕА = А.
Приклад 2 Задані матриці
Знайти існуючі добутки цих матриць.
Розв'язання. У даному випадку згідно умови узгодженості існування добутку матриць, існують лише наступні добутки матриць: АХ (кількість стовпців першого множника - 4 дорівнює кількості рядків другого множника); ВС, СВ, ВА, СА. Знайдемо вказані добутки матриць, використовуючи означення добутку матриць.
розміри: 3х4 4х1 3х1
Відмітимо, що з рівностей (3) та (4) випливає, що матриці В і С не комутують.
Аналогічно можна знайти і добуток СА.
Зауваження 2. Ділення матриць АхВ-1, де В-1 - матриця, обернена до матриці В. Визначення та способи знаходження матриці В-1 розглянемо пізніше, після введення нових необхідних понять.
Зауваження 3. У випадках великого розміру матриць та їх елементів для дій з матрицями використовують комп'ютерну техніку.
|
||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.120.100 (0.009 с.) |

 ;
;  ;
; ;
;  ;
; 

 - діагональна матриця 4 порядку;
- діагональна матриця 4 порядку;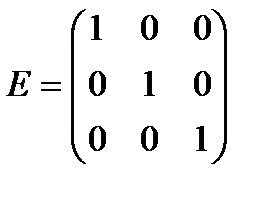 - одинична матриця порядку 3.
- одинична матриця порядку 3.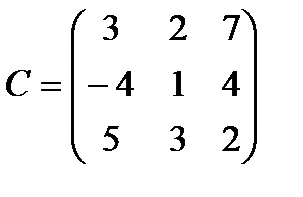 , тоді
, тоді 


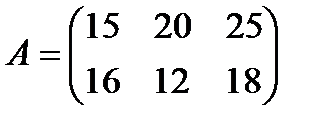 ,
,  , тоді
, тоді
 В матриць А та В існує лише при виконанні умов узгодженості: кількість стовпців матриці А (першого множника) дорівнює кількості рядків матриці В (другого множника).!!!
В матриць А та В існує лише при виконанні умов узгодженості: кількість стовпців матриці А (першого множника) дорівнює кількості рядків матриці В (другого множника).!!!


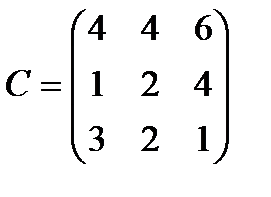



 (3)
(3)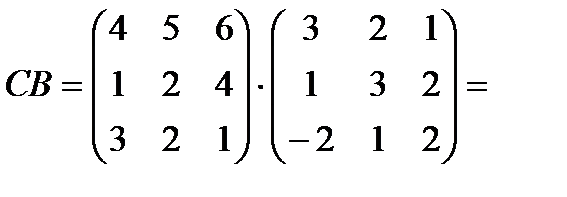
 (4)
(4)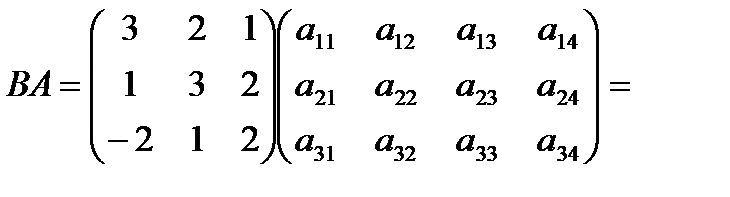
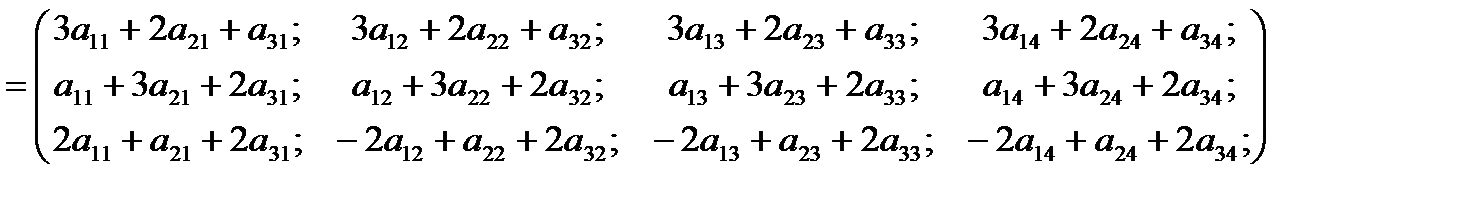
 розглядають як добуток
розглядають як добуток


