
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знання на рівні понять, означень, формулювань.Содержание книги Поиск на нашем сайте
1.1. Геометричний вектор. Дії над векторами. 1.2. Лінійна залежність і незалежність векторів. 1.3. Базис на площині й у просторі. 1.4. Прямокутна декартова система координат. Координати вектора. 1.5. Скалярний добуток двох векторів. 1.6. Векторний добуток двох векторів. 1.7. Мішаний добуток двох векторів.
Уміння в розв’язанні задач. 2.1. Знаходити координати вектора, довжину вектора, орт вектора, кут між векторами. 2.2. Знаходити суму, різницю векторів, їх скалярний та векторний добутки. 2.3. Обчислювати площу трикутника, об’єм піраміди. 2.4. Уміти розкладати вектор за базисними векторами. 2.5.Використовувати умову перпендикулярності двох векторів.
Література: 1. Г.Я. Дутка «Практикум з математики для економістів» – Л. -1998. В. П. Денисюк, В. К. Репета «Вища математика» - К. – 2005. В. М. Буйвол «Елементи лінійної і векторної алгебри та аналітичної геометрії». К -1996 Численные методы. Учебник для техникумов. М. – 1976. Н.В.Богомолов «Практические занятия по математике». М. – 1990.
САМОСТІЙНА РОБОТА №8
Тема 1. Загальні поняття.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Векторна величина на відміну від скалярної задається не лише своїм чисельним значенням, а й напрямом (швидкість, прискорення, сила та ін.). Геометрично вектор являє собою напрямлений відрізок і позначається
Рис.1 Відстань між початком вектора і його кінцем називають довжиною (або модулем) вектора і позначають Вектори, які лежать на одній прямій або паралельних прямих, називають колінеарними.
Рис.2
Вектори
Рис.3 Два вектори називають протилежними, якщо вони колінеарні, мають однакові модулі і протилежні напрями.
Рис.4 Вектор, початок і кінець якого збігаються, називають нуль-вектором. Напрям його не визначений. Вектор, довжина якого дорівнює одиниці, називають одиничним вектором. Одиничний вектор, напрям якого збігається з напрямом вектора Вектори можна вільно переміщувати по площині (у просторі). Тому в аналітичній геометрії їх називають вільними. Кутом між векторами
Рис.5
Три вектори називають компланарними, якщо вони лежать в одній або паралельних площинах. Зокрема, три вектори компланарні, якщо два з них або всі три колінеарні, або хоча б один з них – нуль-вектор.
Лінійні операції над векторами.
До лінійних операцій над векторами належать: 1) додавання (віднімання) векторів; 2) множення вектора на число (скаляр). Сумою векторів
правило трикутника
Суму двох векторів можна будувати також за правилом паралелограма.
Віднімання векторів визначається як дія, обернена додаванню. Різницею векторів
Добутком вектора
Рис.9 З означення множення вектора на число випливає, що коли вектори колінеарні, то існує єдине число
Сформулюємо властивості лінійних операцій над векторами: 1.
3. 4. 5. 6. 7.
Проекція вектора на вісь.
Віссю називають напрямлену пряму, на якій вибрано початок відліку, додатний напрям і одиницю довжини. Проекцією точки А на вісь l називають основу перпендикуляра АА1 (точка А1), опущеного з точки А на вісь l (рис.10).
А Рис.10 А Рис.11
А1
Нехай задано вісь l і вектор
Проекцією вектора Проекцією вектора Кутом між вектором Проекцію вектора
де При цьому Сформулюємо деякі властивості проекцій. 1. Проекція суми кількох векторів на ту саму вісь дорівнює сумі їх проекцій на цю вісь, тобто
2. При множенні вектора
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.92 (0.007 с.) |

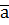 , або
, або  , де точка А – початок вектора, а В – його кінець.
, де точка А – початок вектора, а В – його кінець.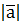 , або
, або  .
.
 .
.
 , який сполучає початок вектора
, який сполучає початок вектора  , який у сумі з вектором
, який у сумі з вектором  називають вектор
називають вектор 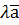 такий, що
такий, що  =
= 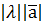 і напрям якого збігається з напрямом вектора
і напрям якого збігається з напрямом вектора 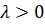 , або протилежний до напряму вектора
, або протилежний до напряму вектора 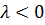 . Так на рис.9 зображено вектори
. Так на рис.9 зображено вектори  , і навпаки, якщо
, і навпаки, якщо  .
.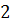 .
.  .
.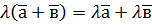 .
.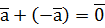 .
. .
. .
.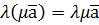 .
. .
. , якщо вісь l і вектор
, якщо вісь l і вектор  однаково напрямлені (рис.10), і від’ємне число
однаково напрямлені (рис.10), і від’ємне число 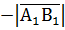 , якщо вісь l і вектор
, якщо вісь l і вектор  (або
(або 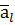 ).
). .
.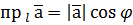
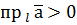 , якщо кут
, якщо кут 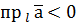 , якщо кут
, якщо кут 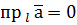 , якщо
, якщо  .
. .
.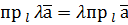 .
.


