
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначники та їх основні властивості.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Квадратній матриці
можна поставити у відповідність певне число, яке називаєься детермінантом або визначником матриці і позначається
Визначник має порядок, який дорівнює порядку відповідної матриці. Поняття детермінанта вводиться лише для квадратних матриць. Діагональ, що йде із лівого верхнього кута визначника, називається головною, а та, що йде із правого верхнього, - побічною. Розглянемо деякий елемент Для визначників 2-го і 3-го порядків існують досить прості правила обчислювання, для інших порядків ми дамо спільне правило обчислювання. 1)
2)
Формули (3.5) називаються розкладом детермінанта за елементами рядка або стовпця і при Приклад 1.
Властивості визначників. 1) Якщо всі елементи деякого рядка чи стовпчика визначника дорівнюють нулю, то і сам визначник дорівнює нулю. 2) Якщо у визначнику поміняти місцями два сусідні рядки чи стовпчики, то знаки таких визначників будуть протилежними, а їх абсолютні величини рівними. 3) Визначник з двома однаковими рядками чи стовпчиками дорівнює нулю. 4) Якщо всі елементи якого-небудь стовпя (рядка) мають спільний множник, то його можна винести за знак визначника. 5) Визначник, елементи двох стовпців (рядків) якого відповідно пропорціональні, дорівнює нулю. 6) Якщо кожний елемент якого-небудь стовпця (рядка) є сумою двох доданків, то визначник дорівнює сумі двох визначників, у яких стовпцями (рядками) є відповідні доданки, а решта збігається із стовпцями (рядками) заданого визачника. 7) Визначник не зміниться, якщо до елементів якого-небудь його стовпця (рядка) додати відповідні елементи іншого стовпця (рядка), помножені на одне і те саме число. 8) Сума добутків елементів
Приклад 4.
1)
3)
6)
7)
4. Правило Крамера для розв`язування систем лінійних рівнянь. Розглянемо систему двох рівнянь з двома невідомими:
Принаймні одне з чисел
Якщо
Узагальненням цього факту буде так зване Правило Крамера. Система
де
Приклад 1. Розв`язати систему рівнянь за методом Крамера:
Розв`язування.
Зауваження. Якщо
Матрицею
Матриця, визначник якої не дорівнює нулю, називається невиродженою. Для того, щоб дана матриця мала обернену, необхідно і достатньо, щоб вона була невиродженою. Щоб знайти матрицю а) знайти визначник даної матриці б) скласти матрицю з алгебраїчних доповнень в) транспонувати її; г) побудувати обернену матрицю за формулою
Приклад 1. Знайти матрицю, обернену до матриці
Розв`язання. Знаходимо визначник
Обчислюємо алгебраїчні доповнення елементів даної матриці:
Щоб переконатися, що результат вірний, треба переконатися, що
Тепер розглянемо систему
де
Оскільки
Приклад 2. Розв`язати матричним способом систему рівнянь
Розв`язання. В нашому випадку
За формулою (5.1) маємо
Отже
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 503; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.006 с.) |

 (3.1)
(3.1) .
.  (3.2)
(3.2) матриці
матриці  , що стоїть на перетині
, що стоїть на перетині  го рядка та
го рядка та 
 го порядку без цього рядка і стовпця. Визначник її називається мінором матриці
го порядку без цього рядка і стовпця. Визначник її називається мінором матриці  . Алгебраїчним доповненням елемента
. Алгебраїчним доповненням елемента  .
.
 (3.3)
(3.3)
 (3.4)
(3.4) визначник дорівнює сумі добутків елементів
визначник дорівнює сумі добутків елементів 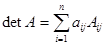 ,
,  (3.5)
(3.5) набувають вигляду (3.3), (3.4).
набувають вигляду (3.3), (3.4).



 2)
2) 
 4)
4)  5)
5) 



 не дорівнює нулю. Нехай це
не дорівнює нулю. Нехай це 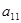 . Тоді маємо
. Тоді маємо .
. розв`язок системи існує і має вигляд
розв`язок системи існує і має вигляд
 (визначник, складений із коефіцієнтов при невідомих) не дорівнює нулю, має один і тільки один розв`язок
(визначник, складений із коефіцієнтов при невідомих) не дорівнює нулю, має один і тільки один розв`язок
 - визначник, утворений із визначника
- визначник, утворений із визначника  (тобто
(тобто 

 За правилом Крамера маємо
За правилом Крамера маємо
 правило Крамера має більш теоретичне значення тому, що виникає необхідність обчислювати
правило Крамера має більш теоретичне значення тому, що виникає необхідність обчислювати  визначників високого порядку, а це займає багато часу.
визначників високого порядку, а це займає багато часу. , оберненою до квадратної матриці
, оберненою до квадратної матриці  називається така, для якоїсправедлива рівність
називається така, для якоїсправедлива рівність .
. , то дана матриця має обернену;
, то дана матриця має обернену; ;
; .
. .
.

 ,
, 
 .
. :
: .
. , (5.1)
, (5.1) ,
,  ,
,  .
.

 і
і  , то
, то .
. .
. .
.
 матриця невироджена і існує обернена
матриця невироджена і існує обернена  .
. .
.



