
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пряма лінія у тривимірному просторі.Содержание книги
Поиск на нашем сайте
Пряма лінія у тривимірному просторі може бути задана перетином двох площин або точкою і напрямом. Загальне рівняння прямої в
(16.1)
Рис.14
Зауважимо, що оскільки пряма (16.1) належить до площин Канонічними рівняннями прямої в де Параметричні рівняння прямої в
де
Рис.15
17. Кут між двома прямими, а також прямою і площиною в Під кутом
II
I
Рис.16 Тому прямі паралельні, якщо їх напрямні вектори
(17.2)
Кутом між прямою і площиною називається один із суміжних кутів Нехай площину і пряму задано відповідно рівняннями
Тоді кути, утворені прямою і площиною, визначаються за формулою
Рис.17
Відповідно площа і пряма паралельні, якщо
і перпендикулярні, якщо
Криві другого порядку. Загальне рівняння кривої другого порядку, що лежить у площині де xoча б одне з чисел Виявляється, що всі криві другого порядку можна поділити на кола, еліпси, гіперболи, параболи та їхні виродження - точки або прямі.
18. Еліпс. Еліпсом називається геометричне місце точок площини, сума відстаней кожної з яких від двох заданих точок цієї самої площини, що називаються фокусами, є величиною сталою і більшою, ніж відстань між фокусами. Нехай на площині дано дві точки Позначимо відстань між фокусами еліпса через Візьмемо довільну точку площини
Це рівняння є аналітичним рівнянням еліпса, але після деяких перетворень в ньому можна звільнитися від ірраціональності і звести до вигляду
де позначено Тепер фокальні радіуси точки
Рис.18
Властивості еліпса:
Гіпербола
Гіперболою називається геометричне місце точок площини, модуль різниці відстаней кожної з яких до двох даних точок, що називаються фокусами, є величиною сталою і меншою за відстань між фокусами. Використаємо прямокутну систему координат і позначення з п.18. Тоді рівняння гіперболи можна записати у вигляді
Згідно з формулами
рівняння гіперболи можна подати у вигляді
Внаслідок перетворень останнього рівняння знаходимо
де Рівняння (19.1) називається канонічним рівнянням гіперболи. Гіпербола складається з двох гілок. Ліва гілка лежить у півплощині Рівняння фокальних радіусів точки гіперболи знаходять так само, як і для еліпса. Дл лівої гілки гіперболи ці рівняння мають
вигляд
а для правої
Рис.19
Властивості гіперболи:
Парабола Нехай на площині дано точку Візьмемо таку систему кординат Нехай Знаходимо
Отже, або
Рис.20
Властивості параболи:
Література
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.122 (0.01 с.) |

 визначає пряму як геометричне місце перетину двох непаралельних площин
визначає пряму як геометричне місце перетину двох непаралельних площин  і
і  :
:













 і
і  і тому напрямний вектор прямої (16.1) можна визначити як
і тому напрямний вектор прямої (16.1) можна визначити як 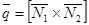 .
.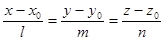 , (16.2)
, (16.2) - точка, що належить цій прямій, а вектор
- точка, що належить цій прямій, а вектор 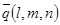 - її напрямний вектор.
- її напрямний вектор. , (16.3)
, (16.3) -параметр, що набуває будь-яких дійсних значень.
-параметр, що набуває будь-яких дійсних значень.


 між двома прямими в
між двома прямими в  і
і  :
: . (17.1)
. (17.1)



 . (17.3)
. (17.3) , утворених даною прямою та її проекцією на цю площину.
, утворених даною прямою та її проекцією на цю площину. і
і  . (17.4)
. (17.4)



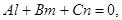 (17.5)
(17.5) (17.6)
(17.6) , має вигляд
, має вигляд 
 відмінно від нуля.
відмінно від нуля. і
і 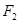 , що називаються фокусами еліпса. Систему координат
, що називаються фокусами еліпса. Систему координат  , тоді
, тоді 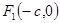 , а
, а  . Величина
. Величина  називається фокальною відстанню. Знайдемо геометричне місце точок, сума відстаней від кожної з яких до даних точок
називається фокальною відстанню. Знайдемо геометричне місце точок, сума відстаней від кожної з яких до даних точок  .
. і
і  . Точка
. Точка 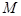 буде точкою еліпса, якщо
буде точкою еліпса, якщо  , де
, де  ,
,  .Тоді дістаємо
.Тоді дістаємо
 , (18.1)
, (18.1) . Рівняння (18.1) називається канонічним рівнянням еліпса.
. Рівняння (18.1) називається канонічним рівнянням еліпса.
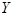

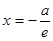


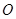




 тобто еліпс є обмеженою кривою.
тобто еліпс є обмеженою кривою. також належать еліпсу. Отже, еліпс має вертикальну та горизонтальну осі симетрії, а також центр симетрії (в канонічній системі координат це осі та початок координат).
також належать еліпсу. Отже, еліпс має вертикальну та горизонтальну осі симетрії, а також центр симетрії (в канонічній системі координат це осі та початок координат). Величини
Величини  називаються відповідно великою та малою осями еліпса, а
називаються відповідно великою та малою осями еліпса, а  - напівосями.
- напівосями. (тобто
(тобто  ), то дістанемо рівняння кола
), то дістанемо рівняння кола 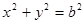 з центром у початку координат і радіусом
з центром у початку координат і радіусом  яке називається ексцентриситетом і характеризує відхилення еліпса від кола – степінь його “витягнутості”. Для кола
яке називається ексцентриситетом і характеризує відхилення еліпса від кола – степінь його “витягнутості”. Для кола  для еліпса
для еліпса 
 назиаються директрисами еліпса. Оскільки
назиаються директрисами еліпса. Оскільки 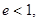 то
то  тобто директриси еліпса лежать поза ним. Характерна особливість директрис полягає в тому, що відношення фокального радіуса будь-якої точки еліпса до відповідної відстані до директриси є величиною сталою, що дорівнює ексцентриситету еліпса:
тобто директриси еліпса лежать поза ним. Характерна особливість директрис полягає в тому, що відношення фокального радіуса будь-якої точки еліпса до відповідної відстані до директриси є величиною сталою, що дорівнює ексцентриситету еліпса: 
 причому
причому 


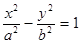 , (19.1)
, (19.1)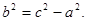
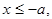 а права – у площині
а права – у площині 



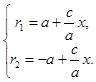






 і пряму
і пряму  яка не проходить через
яка не проходить через 
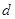 - директрисою.
- директрисою. За означенням
За означенням  тоді точка
тоді точка  а рівнянням директриси є
а рівнянням директриси є 


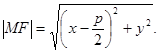

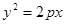 (20.1)
(20.1)





