
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Гаусса розв’язування систем лінійних алгебраїчних рівняньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай задано систему лінійних рівнянь
в якій коефіцієнти Система рівнянь (1.1) може мати єдиний розв`язок, безліч розв`язків, а може не мати жодного розв`язку. Серед цих рівнянь можуть бути такі, що
Якщо Якщо Над системами лінійних рівнянь виконують так звані елементарні перетворення: а) додавання до обох частин рівняння відповідних частин іншого рівняння; б) перестановку рівнянь у системі; в) вилучення із системи тотжності г) множення якого-небудь рівняння системи на дійсне число, відмінне від нуля; д) перенумерування як рівнянь, так і невідомих. Елементарні операції не змінюють множину розв`язків системи лінійних рівнянь. Множину всіх розв`язків системи називають загальним розв`язком, а будь-який елемент цієї множини – частинним розв`язком. Для винаходження загального розв`язку системи (1.1) існує простий і зручний метод Гаусса. Він заснований на тому, що за допомогою елементарних перетворень (1.1) або переконуємося у її несумісності, або одержуємо систему особливого виду: кожне рівняння має невідому, яка надходить до цього рівняння з ненульовим коефіцієнтом, а до інших рівнянь – з коефіцієнтом 0. Якщо в кожному рівнянні зафіксована така невідома, вона називається базисною (всі базисні невідомі утворюють базис невідомих), інші невідомі (якщо такі є) називаються вільними. Приклад 1.
Тут
Очевидно, за наявністю хоча б однієї вільної невідомої система має безліч розв`язків. Якщо ж вільних невідомих немає, розв`язок тільки один. Метод Гаусса (черговий
Процес закінчується тоді, коли всі рівняння перебували в ролі ключового. Тоді із системи, що отримали, легко знаходиться розв`язок. Приклад 2. Розв`язати методом Гаусса систему рівнянь
Розв`язання. Складаємо таблицю із коефіцієнтів при невідомих і вільних членів рівнянь системи. Дужками позначаємо ключовий елемент, за допомогою якого занулюємо інші елементи ключового стовпця (відповідні перетворення записуємо поряд з рядками, наприклад:
Рядки таблиці, що містять лише нульові елементи і відовідають рівнянням 0=0, вилучаємо. Алгоритм метода Гаусса вичерпан, тому що залишилися рядки, які вже були ключовими. Записуємо відповідні рівняння і загальний розв`язок вихідної системи:
Будь-який частинний розв`язок одержуємо із загального, коли надаємо вільним невідомим певних значень, наприклад: при
Приклад 3. Розв`язати методом Гаусса систему
Розв`язання.
Приклад 4. Розв`язання.
Очевидно, що система несумісна тому, що останньому рядку відповідає рівняння Зауваження 1. Частинний розв`язок, у якому всі вільні невідомі дорівнюють нулю, називають базисним. Зауваження 2. Система (1.1) при нульових вільних членах
Матриці і дії над ними. Сукупність
називається матрицею. Елементи матриці мають подвійну нумерацію. Перший індекс вказує номер рядка, другий – стовпчика. Число рядків і стовпчиків вказує на розмір матриці Приклад 1. Прогноз погоди в певних містах може бути подано таблицею 1: Таблиця 1
Числа в таблиці утворюють матрицю розміру Матрицю 1) нульовою, якщо всі елементи дорівнюють нулю 2) додатною, якщо всі елементи 3) від`ємною, якщо всі елементи 4) невід`ємною, якщо всі елементи 5) квадратною, якщо число рядків її дорівнює числу стовпчиків 6) діагональною, якщо вона квадратная і всі елементи, крім діагональних, дорівнюють нулю; 7) одиничною (позначають 8) трикутною, якщо всі її елементи під (над) діагоналлю дорівнюють нулю.
Приклад 2.
Дві матриці однаковіх розмірів з одинаковими відповідними елементами називаються рівними між собою. Добутком матриці Властивості операції множення матриці на число: 1) 2) якщо Сумою двох матриць Властивості операції додавання матриць: 1) 2) 3) 4) Приклад 3. Виконати дії над матрицями
Добутком двох матриць
Властивості операції множення матриць: 1) 2) 3) 4) 5) Приклад 4.
Приклад 5. Систему
Транспонованою матрицею до матриці Приклад 6. Для матриці
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.142.113 (0.008 с.) |


 (1.1)
(1.1) і вільні члени
і вільні члени  - відомі, а
- відомі, а  - невідомі. Розв`язати систему (1.1) – це означає знайти впорядковану сукупність чисел
- невідомі. Розв`язати систему (1.1) – це означає знайти впорядковану сукупність чисел  таку, що при заміні
таку, що при заміні  (1.2)
(1.2) , то рівняня (1.2) не задовільняють ніякі значення
, то рівняня (1.2) не задовільняють ніякі значення  . В цьому разі система не має розв`язку, вона несумісна.
. В цьому разі система не має розв`язку, вона несумісна. , то рівняння (1.2) задавольняють будь-які значення
, то рівняння (1.2) задавольняють будь-які значення  . Тотожність можна вилучити із системи. При цьому решта рівнянь утворює систему, яка матиме ті самі розв`язки, що і (1.1). Такі системи лінійних рівнянь називаються рівносильними.
. Тотожність можна вилучити із системи. При цьому решта рівнянь утворює систему, яка матиме ті самі розв`язки, що і (1.1). Такі системи лінійних рівнянь називаються рівносильними. (1.3)
(1.3) - базисні невідомі,
- базисні невідомі,  - вільні. Загальний розв`язок системи (1.3) одержимо після того, як перепишемо (1.3) у виді:
- вільні. Загальний розв`язок системи (1.3) одержимо після того, як перепишемо (1.3) у виді:
 й крок):
й крок): попередніх кроків, рівняння
попередніх кроків, рівняння  .
. означає, що до четвертого рядка додається другий(ключовий), помножений на
означає, що до четвертого рядка додається другий(ключовий), помножений на  .
.




 .
. маємо частинний розв`язок
маємо частинний розв`язок
 .
.







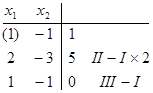

 , яке не має розв`язків.
, яке не має розв`язків. навається однорідною системою лінійних рівнянь. Очевидно, що будь-яка однорідна система завжди сумісна – вона має принаймні один розв`язок
навається однорідною системою лінійних рівнянь. Очевидно, що будь-яка однорідна система завжди сумісна – вона має принаймні один розв`язок 
 чисел
чисел  , записаних у вигляді прямокутної таблиці
, записаних у вигляді прямокутної таблиці
 .
. ,
,  називають
називають ;
; ;
; ;
; ;
; (зокрема, елементи
(зокрема, елементи  називають діагональними);
називають діагональними); ), якщо вона діагональная і всі діагональні елементи дорівнюють одиниці;
), якщо вона діагональная і всі діагональні елементи дорівнюють одиниці;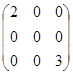 - невід`ємна і діагональна;
- невід`ємна і діагональна; 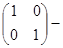 одинична матриця.
одинична матриця. на число
на число  називається матриця
називається матриця  , елементи якої є добутки елементів даної матриці на це число
, елементи якої є добутки елементів даної матриці на це число  для всіх
для всіх 

 , то
, то 
 називають матрицю
називають матрицю  для всіх
для всіх  (комутативність);
(комутативність); (асоціативність);
(асоціативність); (дистрибутивність);
(дистрибутивність);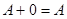 (нейтральність нульової матриці);
(нейтральність нульової матриці);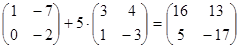
 і
і  називається матриця
називається матриця  , елемент якої
, елемент якої  дорівнює сумі добутків елементів
дорівнює сумі добутків елементів  го рядка матриці
го рядка матриці  -го стовпця матриці
-го стовпця матриці  .
.

 взагалі кажучи;
взагалі кажучи;

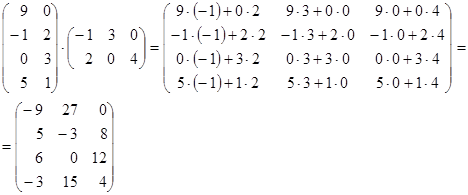
 лінійних рівнянь з
лінійних рівнянь з  невідомими (1.1) можна записати у матричній формі
невідомими (1.1) можна записати у матричній формі де
де  ,
,  .
. 
 транспонованою буде
транспонованою буде 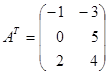 .
.


