
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи рішення систем нелінійних алгебраїчних рівняньСодержание книги
Поиск на нашем сайте
Обчислення при рішенні СНАР складаються з декількох вкладених один в іншій циклічних процесів. Зовнішній цикл – цикл покрокового чисельного інтегрування, параметром циклу є номер кроку. Якщо модель аналізованого об’єкта нелінійна, то на кожному кроці виконується проміжний цикл – ітераційний цикл рішення системи нелінійних алгебраїчних рівнянь (СНАР). Параметр циклу – номер ітерації. У внутрішньому циклі вирішується система лінійних алгебраїчних рівнянь (СЛАР), наприклад, при застосуванні вузлового методу формування ММС такою системою є
де Для рішення систем алгебраїчних рівнянь можна застосовувати прямі ітераційні методи. До них відносяться методи простої ітерації, Зейделя, Якобі, релаксації. Для них необхідне виконання жорстких умов збіжності, характерна порівняно повільна збіжність. Тому в сучасних програмах аналізу найбільше поширення одержав метод Ньютона, заснований на лінеаризації СНАР. Сама модель (3.18) отримана саме відповідно до методу Ньютона. Основна перевага методу Ньютона – висока швидкість збіжності. Представимо СНАР у вигляді
Розкладаючи
де Обчислювальний процес стартує з початкового наближення
Однак метод Ньютона не завжди приводить до збіжних ітерацій. Умови збіжності методу Ньютона виражаються досить складно, але існує легко використовуваний підхід до поліпшення збіжності. Це близькість початкового наближення до шуканого кореня СНАР. Використання цього фактору привело до появи методу рішення СНАР, називаного продовженням рішення по параметрі. У методі продовження рішення по параметрі в ММС виділяється деякий параметр Як параметр В цих умовах очевидна доцільність подання математичних моделей для аналізу статичних станів у вигляді СНАР, як і для динамічного аналізу. До інших методів рішення систем алгебраїчних рівнянь, використовуваним у математичному забезпеченні САПР, відносяться методи простої ітерації, Зейделя, Якобі, релаксації. Відповідно до методу простої ітерації обчислення виконують по формулі
причому для забезпечення збіжності параметр Метод Зейделя відрізняється від методу простої ітерації тим, що права частина ітераційної формули (3.24) обновляється відразу ж після обчислення чергового елемента вектора Відповідно до методу Якобі обчислення виконують по формулі
де
Аналіз у частотній області Аналіз у частотній області більш специфічний у порівнянні з аналізом у часовій області. Його застосовують, як правило, до об’єктів з лінеаризуємимі ММ при дослідженні коливальних стаціонарних процесів, аналізі стійкості, розрахунку перекручувань інформації, що представляється спектральними складових сигналів, і т.п. Аналіз у частотній області виконується відповідно лінеарізованим моделям об’єктів. Для лінійних СЛАР справедливе застосування для алгебраізації диференціальних рівнянь перетворення Фур’є, у якому оператор Характерною особливістю є комплексний характер матриці коефіцієнтів, що до деякої міри ускладнює процедуру рішення, але не створює принципових труднощів. При рішенні задають ряд частот Багатоваріантний аналіз Одноваріантний аналіз дозволяє одержати інформацію про стан і поводження проектованого об’єкта в одній точці простору внутрішніх Найчастіше багатоваріантний аналіз у САПР виконується в інтерактивному режимі, коли розроблювач неодноразово міняє в математичній моделі ті або інші параметри із множин Областю працездатності називають область у просторі аргументів, у межах якої виконуються всі задані умови працездатності, тобто значення всіх вихідних параметрів перебувають у припустимі по ТЗ межах. Серед процедур багатоваріантного аналізу можна виділити типові, виконувані по заздалегідь складених програмах. До таких процедур ставляться аналіз чутливості й статистичний аналіз. Найбільш просто аналіз чутливості реалізується шляхом чисельного диференціювання. Нехай аналіз проводиться в деякій точці
Такий метод чисельного диференціювання називають методом приростів. Для аналізу чутливості, відповідно до методу приростів, потрібно виконати Аналіз чутливості – це розрахунок векторів градієнтів вихідних параметрів, що входить складовою частиною в програми параметричної оптимізації, що використають градієнтні методи. Ціль статистичного аналізу — оцінка законів розподілу вихідних параметрів і (або) числових характеристик цих розподілів. Випадковий характер величин
Рис. 2. Результат статистичного аналізу.
У САПР статистичний аналіз здійснюється чисельним методом — методом Монте-Карло (статистичних випробувань). Відповідно до цього методу виконуються · гістограми вихідних параметрів; · оцінки математичних очікувань і дисперсій вихідних параметрів: · оцінки коефіцієнтів кореляції й регресії між обраними вихідними й внутрішніми параметрами, які, зокрема, можна використати для оцінки коефіцієнтів чутливості. Статистичний аналіз, виконуваний відповідно до методу Монте-Карло, — трудомістка процедура, оскільки число випробувань Більш типова ситуація, коли закони розподіли
Однак варто помітити, що, проводячи аналіз на найгірший випадок, можна одержати завищені значення розкиду вихідних параметрів, і якщо домагатися виконання умов працездатності в найгірших випадках, те це часто веде до невиправданого збільшення вартості, габаритних розмірів, маси й інших показників проектованих конструкцій, хоча й гарантує із запасом виконання умов працездатності.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.212.146 (0.008 с.) |


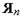 — матриця Якобі,
— матриця Якобі,  — вектор правих частин. Тому в математичне забезпечення аналізу на макрорівні входять методи рішення СНАР й СЛАР.
— вектор правих частин. Тому в математичне забезпечення аналізу на макрорівні входять методи рішення СНАР й СЛАР.
 в ряд Тейлора біля деякої точки
в ряд Тейлора біля деякої точки  , одержуємо
, одержуємо
 :
:
 — матриця Якобі. Рішення системи (3.20) дає чергове наближення до кореня системи (3.19), що зручно позначити
— матриця Якобі. Рішення системи (3.20) дає чергове наближення до кореня системи (3.19), що зручно позначити  .
. й у випадку збіжності ітерацій закінчується, коли погрішність, оцінювана як
й у випадку збіжності ітерацій закінчується, коли погрішність, оцінювана як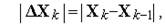
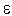 .
.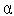 , такий, що при
, такий, що при  корінь
корінь 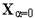 системи (3.19) відомий, а при збільшенні
системи (3.19) відомий, а при збільшенні  до його дійсного значення складові вектора
до його дійсного значення складові вектора  плавно змінюються від
плавно змінюються від 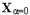 до дійсного значення кореня. Тоді задача розбивається на ряд подзадач, послідовно розв’язуваних при послідовних значеннях
до дійсного значення кореня. Тоді задача розбивається на ряд подзадач, послідовно розв’язуваних при послідовних значеннях 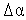 зміни
зміни  . Очевидно, що при
. Очевидно, що при  корінь СНАР дорівнює значенню вектора невідомих на попередньому кроці. Регулювання значень
корінь СНАР дорівнює значенню вектора невідомих на попередньому кроці. Регулювання значень  покладають на алгоритм автоматичного вибору кроку.
покладають на алгоритм автоматичного вибору кроку.
 потрібно вибирати з умови
потрібно вибирати з умови 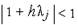 для будь-якого
для будь-якого  де
де 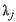 —
—  -е власне значення матриці Якобі.
-е власне значення матриці Якобі. .
.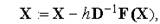
 — діагональ матриці Якобі системи рівнянь (3.18).
— діагональ матриці Якобі системи рівнянь (3.18). заміняється на оператор
заміняється на оператор 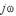 .
.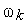 . Для кожної частоти вирішують СЛАР й визначають дійсні й мнимі частини шуканих фазових змінних. По них визначають амплітуду й фазовий кут кожної спектральної складової, що й дозволяє побудувати амплітудно-частотні характеристики, знайти власні частоти коливальної системи й т.п.
. Для кожної частоти вирішують СЛАР й визначають дійсні й мнимі частини шуканих фазових змінних. По них визначають амплітуду й фазовий кут кожної спектральної складової, що й дозволяє побудувати амплітудно-частотні характеристики, знайти власні частоти коливальної системи й т.п. параметрів. Очевидно, що для оцінки властивостей проектованого об’єкта цього недостатньо. Потрібно виконувати багатоваріантний аналіз, тобто досліджувати поводження об’єкта у ряді точок згаданого простору, що для стислості будемо далі називати простором аргументів.
параметрів. Очевидно, що для оцінки властивостей проектованого об’єкта цього недостатньо. Потрібно виконувати багатоваріантний аналіз, тобто досліджувати поводження об’єкта у ряді точок згаданого простору, що для стислості будемо далі називати простором аргументів.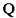 , виконує одноваріантний аналіз і фіксує отримані значення вихідних параметрів. Подібний багатоваріантний аналіз дозволяє оцінити області працездатності, ступінь виконання умов працездатності, а отже, ступінь виконання ТЗ на проектування, розумність прийнятих проміжних рішень по зміні проекту й т.п.
, виконує одноваріантний аналіз і фіксує отримані значення вихідних параметрів. Подібний багатоваріантний аналіз дозволяє оцінити області працездатності, ступінь виконання умов працездатності, а отже, ступінь виконання ТЗ на проектування, розумність прийнятих проміжних рішень по зміні проекту й т.п. простору аргументів, у якій попередньо проведений одноваріантний аналіз і знайдені значення вихідних параметрів
простору аргументів, у якій попередньо проведений одноваріантний аналіз і знайдені значення вихідних параметрів  . Виділяється
. Виділяється  параметрів-аргументів
параметрів-аргументів 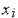 (із числа елементів векторів
(із числа елементів векторів 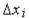 , виконується одноваріантний аналіз, фіксуються значення вихідних параметрів
, виконується одноваріантний аналіз, фіксуються значення вихідних параметрів 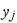 і підраховуються значення абсолютних
і підраховуються значення абсолютних

 раз одноваріантний аналіз. Результат його застосування — матриці абсолютної й відносної чутливості, елементами яких є коефіцієнти
раз одноваріантний аналіз. Результат його застосування — матриці абсолютної й відносної чутливості, елементами яких є коефіцієнти  й
й 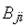 .
. , тому вихідними даними для статистичного аналізу є відомості про закони розподілу
, тому вихідними даними для статистичного аналізу є відомості про закони розподілу  . Відповідно до результатів статистичного аналізу прогнозують такий важливий виробничий показник, як відсоток бракованих виробів у готовій продукції (Рис. 2). На малюнку представлена розрахована щільність
. Відповідно до результатів статистичного аналізу прогнозують такий важливий виробничий показник, як відсоток бракованих виробів у готовій продукції (Рис. 2). На малюнку представлена розрахована щільність  розподілу вихідного параметра
розподілу вихідного параметра  , що має умову працездатності
, що має умову працездатності  , затемнена ділянка характеризує частку виробів, що не задовольняють умові працездатності параметра
, затемнена ділянка характеризує частку виробів, що не задовольняють умові працездатності параметра 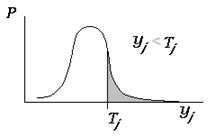
 статистичних випробувань, кожне статистичне випробування являє собою одноваріантний аналіз, виконуваний при випадкових значеннях параметрів-аргументів. Ці випадкові значення вибирають відповідно до заданих законів розподілу аргументів
статистичних випробувань, кожне статистичне випробування являє собою одноваріантний аналіз, виконуваний при випадкових значеннях параметрів-аргументів. Ці випадкові значення вибирають відповідно до заданих законів розподілу аргументів  . Отримані в кожному випробуванні значення вихідних параметрів накопичують, після
. Отримані в кожному випробуванні значення вихідних параметрів накопичують, після  параметрів
параметрів  (такі відхилення часто вказуються в паспортних даних на комплектуючі деталі). У таких випадках більш реалістично застосовувати метод аналізу на найгірший випадок. Відповідно до цього методу, спочатку виконують аналіз чутливості з метою визначення знаків коефіцієнтів чутливості. Далі здійснюють
(такі відхилення часто вказуються в паспортних даних на комплектуючі деталі). У таких випадках більш реалістично застосовувати метод аналізу на найгірший випадок. Відповідно до цього методу, спочатку виконують аналіз чутливості з метою визначення знаків коефіцієнтів чутливості. Далі здійснюють  раз одноваріантний аналіз, де
раз одноваріантний аналіз, де 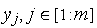 . Так, якщо
. Так, якщо  й коефіцієнт чутливості позитивний (тобто
й коефіцієнт чутливості позитивний (тобто  ) або
) або 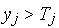 й
й 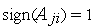 , то
, то




