
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вихідні рівняння для формування моделей на макрорівніСодержание книги
Поиск на нашем сайте
Вихідний математичний опис процесів в об'єктах на макрорівні представлено системами звичайних диференціальних і алгебраїчних рівнянь. Аналітичні рішення таких систем при типових значеннях їхніх порядків у практичних задачах одержати не вдається, тому в САПР переважно використовуються алгоритмічні моделі. У цьому параграфі викладений узагальнений підхід до формування алгоритмічних моделей на макрорівні, справедливий для більшості застосувань. Вихідними для формування математичних моделей об'єктів на макрорівні є компонентні й топологічні рівняння. Компонентними рівняннями називають рівняння, що описують властивості елементів (компонентів), інакше кажучи, математична модель елемента (ММЕ) представляється компонентними рівняннями. Топологічні рівняння описують взаємозв'язки в складі системи, що моделюється. У сукупності компонентні й топологічні рівняння конкретної фізичної системи являють собою вихідну математичну модель системи (ММС). Очевидно, що компонентні й топологічні рівняння в системах різної фізичної природи відбивають різні фізичні властивості, але можуть мати однаковий формальний вид. Однакова форма запису математичних співвідношень дозволяє говорити про формальні аналогії компонентних і топологічних рівнянь. Такі аналогії існують для механічних поступальних, механічних обертальних, електричних, гідравлічних (пневматичних), теплових об'єктів. Наявність аналогій приводить до практично важливого висновку: значна частина алгоритмів формування й дослідження моделей у САПР виявляється інваріантною й може бути застосована до аналізу проектованих об'єктів у різних предметних областях. Єдність математичного апарата формування ММС особливо зручно при аналізі систем, що складаються з фізично різнорідних підсистем. У перерахованих вище застосуваннях компонентні рівняння мають вигляд:
топологічні рівняння:
де Розрізняють фазові змінні двох типів, їхні узагальнені найменування — фазові змінні типу потенціалу (наприклад, електрична напруга) і фазові змінні типу потоку (наприклад, електричний струм). Кожне компонентне рівняння характеризує зв'язки між різнотипними фазовими змінними, стосовними до одного компонента (наприклад, закон Ома описує зв'язок між напругою й струмом у резисторі), а топологічне рівняння – зв'язку між однотипними фазовими змінними в різних компонентах. Моделі можна представляти у вигляді систем рівнянь або в графічній формі, якщо між цими формами встановлена взаємно однозначна відповідність. Як графічна форма часто використають еквівалентні схеми. Нижче розглянемо приклади компонентних і топологічних рівнянь для різних типів систем.
Механічні системи
Фазовими змінними в механічних поступальних системах є сили й швидкості. Використовують одну із двох можливих електромеханічних аналогій. Надалі будемо використати ту з них, у якій швидкість відносять до фазових змінних типу потенціалу, а силу вважають фазовою змінною типу потоку. З огляду на формальний характер подібних аналогій, рівною мірою можна застосовувати й протилежну термінологію. Компонентне рівняння, що характеризує інерційні властивості тіл, у силу другого закону Ньютона має вигляд:
де Пружні властивості тіл описуються компонентним рівнянням, яке можна одержати з рівняння закону Гука. В одномірному випадку (якщо розглядаються поздовжні деформації пружного стрижня):
де
де Диссипативні властивості в механічних системах твердих тіл виражаються співвідношеннями, що характеризують зв'язок між силою тертя й швидкістю взаємного переміщення тіл, причому в цих співвідношеннях похідні сил або швидкостей не фігурують. Топологічні рівняння характеризують, по-перше, закон рівноваги сил: сума сил, прикладених до тіла, включаючи силу інерції, дорівнює нулю (принцип Даламбера), по-друге, закон швидкостей, відповідно до якого сума відносної, переносної й абсолютної швидкостей дорівнює нулю. У механічних обертальних системах справедливі компонентні й топологічні рівняння поступальних систем із заміною поступальних швидкостей на кутові, сил – на обертальні моменти, мас – на моменти інерції, жорсткостей – на обертальні жорсткості. Є істотна відмінність у моделюванні електричних і механічних систем: перші з них одномірні, а процеси в других часто доводиться розглядати у двох- (2D) або тривимірному (3D) просторі. Отже, при моделюванні механічних систем у загальному випадку в просторі 3D потрібно використовувати векторне зображення фазових змінних, кожна з яких має шість складових, відповідним шести ступеням свободи. Однак відзначені вище аналогії залишаються справедливими, якщо їх відносити до проекцій сил і швидкостей на кожну просторову вісь, а при графічному зображенні моделей використовувати шість еквівалентних схем – три для поступальних складових і три для обертальних.
Гідравлічні системи
Фазовими змінними в гідравлічних системах є витрати й тиски. Як і в попередньому випадку, компонентні рівняння описують властивості рідини розсіювати або накопичувати енергію. Розглянемо компонентні рівняння для рідини на лінійній ділянці трубопроводу довжиною
Тут Явище стискальності рідини описується компонентним рівнянням, що випливає із закону Гука:
Диференціюючи (3.7) і з огляду на, що об'ємна витрата
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

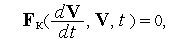

 — вектор фазових змінних,
— вектор фазових змінних, 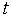 — час.
— час.
 — сила;
— сила; 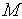 — маса;
— маса;  — поступальна швидкість.
— поступальна швидкість.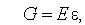
 — механічна напруга;
— механічна напруга;  — модуль пружності;
— модуль пружності; 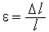 — відносна деформація;
— відносна деформація;  — зміна довжини
— зміна довжини  пружного тіла під впливом
пружного тіла під впливом  . З огляду на, що
. З огляду на, що  , де
, де  — сила,
— сила,  — площа поперечного переріза тіла, і диференціюючи (3.4), маємо:
— площа поперечного переріза тіла, і диференціюючи (3.4), маємо:
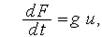
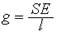 — жорсткість (величину, зворотню жорсткості, іноді називають гнучкістю
— жорсткість (величину, зворотню жорсткості, іноді називають гнучкістю  ),
),  — швидкість.
— швидкість. й скористаємося рівнянням Нав’є-Стоксу в наступній його формі (для ламінарної течії рідини):
й скористаємося рівнянням Нав’є-Стоксу в наступній його формі (для ламінарної течії рідини):
 — щільність рідини;
— щільність рідини; 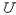 — швидкість;
— швидкість;  — тиск;
— тиск;  — коефіцієнт лінеаризованого в’язкого тертя. Враховуючи, що
— коефіцієнт лінеаризованого в’язкого тертя. Враховуючи, що  , де
, де  — об'ємна витрата;
— об'ємна витрата;  — площа поперечного переріза трубопроводу, та, заміняючи просторову похідну відношенням кінцевих різностей, маємо:
— площа поперечного переріза трубопроводу, та, заміняючи просторову похідну відношенням кінцевих різностей, маємо: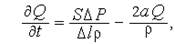

 — падіння тиску на розглянутій ділянці трубопроводу;
— падіння тиску на розглянутій ділянці трубопроводу;  — гідравлічна індуктивність, що відображає інерційні властивості рідини;
— гідравлічна індуктивність, що відображає інерційні властивості рідини; 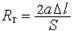 — гідравлічний опір, що відображає в’язке тертя.
— гідравлічний опір, що відображає в’язке тертя.
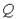 зв'язана зі швидкістю
зв'язана зі швидкістю  співвідношенням
співвідношенням  , одержуємо:
, одержуємо:
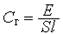 — гідравлічна ємність.
— гідравлічна ємність.


