
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи й алгоритми комп'ютерної графікиСодержание книги
Поиск на нашем сайте До методів комп'ютерної графіки відносять методи перетворення графічних об'єктів, виведення (розгорнення) ліній у растровій формі, виділення вікна, видалення схованих ліній, проектування, зафарбування зображень. Перетворення графічних об'єктів виконується за допомогою операцій переносу, масштабування, повороту. Перенос точки з положення
де Таблиця 4
Для операцій масштабування й повороту матриці Зручність (4.1) пояснюється тим, що будь-яку комбінацію елементарних перетворень можна описати формулою (4.1). Наприклад, вираження для переміщення з одночасним поворотом має вигляд
Таблиця 5
Таблиця 6
Вивід графічних елементів у растровій формі потрібно для відображення цих елементів на бітову карту растрової відеосистеми. Нехай потрібно розгорнути відрізок 1. 2. 3. якщо 4. 5. перехід до пункту 3, поки не досягнута точка Економічність цього алгоритму обумовлюється відсутністю довгих арифметичних операцій типу множення. Виділення вікна потрібно при визначенні тієї частини сцени, що повинна бути виведена на екран дисплея. Нехай вікно обмежене лініями 1. якщо 2. якщо 3. якщо 4. якщо Після закінчення перегляду стосовно до всіх границь у вікні виявляються вершини, що залишилися в списку.
Рис. 4. Виділення вікна Застосовуючи ці правила в нашому прикладі, одержуємо спочатку багатокутник Застосовують ряд алгоритмів видалення схованих ліній. Один з найбільше просто реалізованих алгоритмів — алгоритм z-буфера, де z-буфер — область пам'яті, число осередків у якій дорівнює числу пікселів у вікні виводу. Передбачається, що вісь На початку виконання алгоритму всі пікселі відповідають максимальному значенню Алгоритми побудови проекцій перетворюють тривимірні зображення у двовимірні. У випадку побудови центральної проекції кожна точка тривимірного зображення відображається на картинну поверхню шляхом перерахування координат
Рис. 5. Побудова центральної проекції точки A
У паралельних проекціях Моделювання ефектів відбиття світла від поверхні об'єкта в геометричних моделях називають рендерінгом. Зафарбування матових поверхонь засновані на законі Ламберта, відповідно до якого яскравість відбитого від поверхні світла пропорційні
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

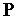 в нове положення
в нове положення  можна виконувати по формулах типу
можна виконувати по формулах типу
 — приріст по координаті
— приріст по координаті  . Однак зручніше операції перетворення представляти в єдиній матричній формі
. Однак зручніше операції перетворення представляти в єдиній матричній формі
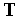 — перетворююча матриця. При цьому крапки
— перетворююча матриця. При цьому крапки  . Тоді перенос для випадку 2D можна виразити у вигляді (4.1), де
. Тоді перенос для випадку 2D можна виразити у вигляді (4.1), де  .
.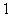



 ,
,  — масштабні множники,
— масштабні множники,  — кут повороту.
— кут повороту.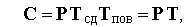
 ,
,  — матриця переміщення,
— матриця переміщення,  — матриця повороту.
— матриця повороту.


 прямої
прямої  , причому
, причому  (при інших значеннях
(при інших значеннях  розглянутий нижче алгоритм залишається справедливим після певних модифікацій). Уведемо позначення:
розглянутий нижче алгоритм залишається справедливим після певних модифікацій). Уведемо позначення: 
 за величину дискрета (пікселя) приймемо одиницю. В алгоритмі розгорнення номера рядків і стовпців карти, на перетинанні яких повинні перебувати точки відрізка, визначаються в такий спосіб:
за величину дискрета (пікселя) приймемо одиницю. В алгоритмі розгорнення номера рядків і стовпців карти, на перетинанні яких повинні перебувати точки відрізка, визначаються в такий спосіб:

 , то
, то 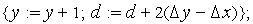 інакше
інакше 

 .
.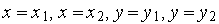 (Рис. 4). По черзі для кожного багатокутника перевіряється розташування його вершин і ребер щодо границь вікна. Так, для багатокутника
(Рис. 4). По черзі для кожного багатокутника перевіряється розташування його вершин і ребер щодо границь вікна. Так, для багатокутника  (див. Рис. 4) при відсіканні по границі
(див. Рис. 4) при відсіканні по границі  проглядається множина вершин у порядку обходу по годинній стрілці. Можливі чотири ситуації для двох послідовних вершин
проглядається множина вершин у порядку обходу по годинній стрілці. Можливі чотири ситуації для двох послідовних вершин  :
: й
й  , то обидві вершини й інцидентне їм ребро перебувають поза вікном і виключаються з подальшого аналізу;
, то обидві вершини й інцидентне їм ребро перебувають поза вікном і виключаються з подальшого аналізу; й
й 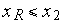 , то обидві вершини й інцидентне їм ребро залишаються для подальшого аналізу;
, то обидві вершини й інцидентне їм ребро залишаються для подальшого аналізу; в нашому прикладі такою новою вершиною буде
в нашому прикладі такою новою вершиною буде  ;
;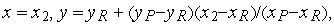 а вершина
а вершина  .
.
 , а після відсікання по верхній границі
, а після відсікання по верхній границі  — багатокутник
— багатокутник  (див. рис. 4). Однак правильний результат трохи інший, а саме багатокутник
(див. рис. 4). Однак правильний результат трохи інший, а саме багатокутник  . Цей правильний результат виходить при подвійному обході вершин спочатку по годинній стрілці, потім проти із включенням у список нових вершин, що з'являються при кожному обході.
. Цей правильний результат виходить при подвійному обході вершин спочатку по годинній стрілці, потім проти із включенням у список нових вершин, що з'являються при кожному обході. спрямована по нормалі до видової поверхні й спостерігач розташований у крапці
спрямована по нормалі до видової поверхні й спостерігач розташований у крапці  .
. ), вибирається точка з найменшим значенням
), вибирається точка з найменшим значенням  і
і 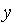 (Рис. 5). Так, координату
(Рис. 5). Так, координату 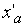 точки
точки  обчислюють по очевидній формулі
обчислюють по очевидній формулі
 точки
точки 
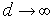 і координати
і координати 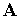 збігаються. Тому побудова паралельних проекцій зводиться до виділення вікна, при необхідності до повороту зображення й можливо до видалення схованих ліній.
збігаються. Тому побудова паралельних проекцій зводиться до виділення вікна, при необхідності до повороту зображення й можливо до видалення схованих ліній. , де
, де 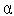 — кут між нормаллю до поверхні й напрямком луча падаючого світла. В алгоритмі Гуро яскравість внутрішніх точок розглянутої поверхні визначається лінійною інтерполяцією яскравості у вершинах багатокутника. При цьому спочатку проводиться інтерполяція в крапках ребер, а потім по рядках горизонтального розгорнення. Більш реалістичними виходять зображення в алгоритмі Фонга, заснованому на лінійній інтерполяції векторів нормалей до поверхні. Один з алгоритмів рендерінгу полягає в трасуванні променів — моделюванні проходження променів світла між джерелами, поверхнями й спостерігачем.
— кут між нормаллю до поверхні й напрямком луча падаючого світла. В алгоритмі Гуро яскравість внутрішніх точок розглянутої поверхні визначається лінійною інтерполяцією яскравості у вершинах багатокутника. При цьому спочатку проводиться інтерполяція в крапках ребер, а потім по рядках горизонтального розгорнення. Більш реалістичними виходять зображення в алгоритмі Фонга, заснованому на лінійній інтерполяції векторів нормалей до поверхні. Один з алгоритмів рендерінгу полягає в трасуванні променів — моделюванні проходження променів світла між джерелами, поверхнями й спостерігачем.


