
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вибір методів аналізу в часовій областіСодержание книги
Поиск на нашем сайте Аналіз процесів у проектованих об'єктах можна робити в часовій і частотній областях. Аналіз у часовій області (динамічний аналіз) дозволяє одержати картину перехідних процесів, оцінити динамічні властивості об'єкта, він є важливою процедурою при дослідженні як лінійних, так і нелінійних систем. Методи аналізу в часовій області, використовувані в універсальних програмах аналізу в САПР, — це чисельні методи інтегрування систем звичайних диференціальних рівнянь (СЗДР):
Інакше кажучи, це методи алгебраізації диференціальних рівнянь. Формули інтегрування СЗДР можуть входити в математичну модель (ММ) незалежно від компонентних рівнянь або бути інтегрованими в ММ компонентів, як це виконано у вузловому методі. Від вибору методу рішення СЗДР істотно залежать такі характеристики аналізу, як точність і обчислювальна ефективність. Ці характеристики визначаються насамперед типом і порядком обраного методу інтегрування СЗДР. Застосовують два типи методів інтегрування — явні методи (інакше екстраполяційні або методи, засновані на формулах інтегрування вперед), і неявні методи (інтерполяційні, засновані на формулах інтегрування назад). Розходження між ними зручно показати на прикладі найпростіших методів першого порядку — методів Ейлеру. Формула явного методу Ейлеру являє собою наступну формулу заміни похідних у точці
Виконаємо порівняльний аналіз явних і неявних методів на прикладі модельної задачі:
при ненульових початкових умовах При алгебраізації явним методом маємо
Позначимо
і застосуємо перетворення подоби для матриці
Точне рішення модельної задачі (3.8)
у зв’язку з тим, що
Відомо, що для фізично стійких систем власні значення матриці коефіцієнтів у ММС виявляються зі знаком мінус. Якщо до того ж всі
де Якщо порушено умову (3.12), то відбувається втрата стійкості обчислень, а це означає, що в рішенні задачі виникають помилкові коливання з амплітудою, що збільшується від кроку до кроку, і швидким аварійним остановом ЕОМ внаслідок переповнення розрядної сітки. Звичайно, ні про яку адекватність рішення говорити не доводиться. Для дотримання (3.12) застосовують ті або інші алгоритми автоматичного вибору кроку. Відзначимо, що в складній моделі розрахунок Умова (3.12) накладає жорсткі обмеження на крок інтегрування. У результаті обчислювальна ефективність явних методів різко падає з погіршенням обумовленості ММС. Справді, тривалість
Відношення Аналогічний аналіз числової стійкості неявних методів дає наступні результати. Замість (3.9) маємо
Метод інтегрування СЗДР називають A-стійким, якщо погрішність інтегрування залишається обмеженою при будь-якому кроці Застосування A-стійких методів дозволяє істотно зменшити необхідні числа кроків Вибір порядку методу рішення СЗДР досить простий: по-перше, більше високий порядок забезпечує більше високу точність, по-друге, серед неявних різницевих методів, крім методу Ейлеру, A-стійкі також методи другого порядку й серед них – метод трапецій. Тому переважне поширення в програмах аналізу одержали методи другого порядку – модифікації методу трапецій.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |


 :
:
 — розмір кроку інтегрування (звичайно
— розмір кроку інтегрування (звичайно  називають просто кроком інтегрування). У формулі неявного методу Ейлеру використане диференціювання назад:
називають просто кроком інтегрування). У формулі неявного методу Ейлеру використане диференціювання назад:
 .
.
 і при використанні методів Ейлера з постійним кроком
і при використанні методів Ейлера з постійним кроком  . Тут
. Тут  — постійна матриця;
— постійна матриця;  — вектор фазових змінних.
— вектор фазових змінних.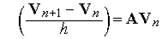

 — одинична матриця. Вектор
— одинична матриця. Вектор  можна виразити через вектор початкових умов
можна виразити через вектор початкових умов  :
:

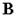

 — перетворююча матриця;
— перетворююча матриця;  — діагональна матриця із власними значеннями
— діагональна матриця із власними значеннями 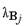 матриці
матриці 

 , отже, умовою стійкості процесу чисельного рішення можна вважати
, отже, умовою стійкості процесу чисельного рішення можна вважати

 , та
, та  , оскільки
, оскільки  , та
, та  й умова стійкості
й умова стійкості
 вещественні величини (характер процесів у ММС із моделлю (3.8) аперіодичний), то природно визначити постійні часу фізичної системи як
вещественні величини (характер процесів у ММС із моделлю (3.8) аперіодичний), то природно визначити постійні часу фізичної системи як


 — мінімальна постійна часу. Якщо використати явні методи більш високого порядку, то може збільшитися коефіцієнт перед
— мінімальна постійна часу. Якщо використати явні методи більш високого порядку, то може збільшитися коефіцієнт перед  моделюємого процесу повинна бути порівнянною із часом заспокоєння системи після збудливого впливу, тобто порівнянна з максимальною постійною часу
моделюємого процесу повинна бути порівнянною із часом заспокоєння системи після збудливого впливу, тобто порівнянна з максимальною постійною часу  . Необхідне число кроків інтегрування дорівнює
. Необхідне число кроків інтегрування дорівнює
 називають розкидом постійних часу або числом обумовленості. Більше строго число обумовленості матриці
називають розкидом постійних часу або числом обумовленості. Більше строго число обумовленості матриці  визначається як
визначається як  , а число обумовленості системи рівнянь
, а число обумовленості системи рівнянь  як
як  Чим більше це число, тим гірше обумовленість. Спроби застосування явних методів до різних ММС найчастіше приводять до неприпустимо низької обчислювальної ефективності, оскільки в реальних моделях
Чим більше це число, тим гірше обумовленість. Спроби застосування явних методів до різних ММС найчастіше приводять до неприпустимо низької обчислювальної ефективності, оскільки в реальних моделях  — звичайна ситуація. Тому в цей час в універсальних програмах аналізу явні методи рішення СЗДР не застосовують.
— звичайна ситуація. Тому в цей час в універсальних програмах аналізу явні методи рішення СЗДР не застосовують.

 . Отже, неявний метод Ейлера має так називану A-стійкість.
. Отже, неявний метод Ейлера має так називану A-стійкість. .
. . У цих методах крок вибирається автоматично не з умов стійкості, а тільки з міркувань точності рішення.
. У цих методах крок вибирається автоматично не з умов стійкості, а тільки з міркувань точності рішення.


