
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод скінченних елементів для аналізу механічної міцностіСодержание книги
Поиск на нашем сайте
Як вихідне положення в методі скінченних елементів приймають варіаційний принцип Лагранжа (принцип потенційної енергії), відповідно до якого рівноважний стан, у який може прийти система, характеризується мінімумом потенційної енергії. Потенційна енергія У свою чергу, у сталому стані
де Деформації
де
де Деформації й напруги зв’язані між собою за допомогою матриці
Фігуруючі у Табл. 3 коефіцієнт
Підставляючи (3.28) і (3.27) в (3.25), одержуємо
Таблиця 3
Рішенням задачі повинне бути поле переміщень Замінюючи
де Відповідно до принципу потенційної енергії в стані рівноваги маємо
де Матриця жорсткості виявляється сильно розрідженою, тому для рішення (3.30) застосовують методи розріджених матриць. Одним із широко відомих методів розріджених матриць є метод прогону, застосовуваний у випадку тридіагональних матриць коефіцієнтів у системі алгебраїчних рівнянь.
Для рішення розподілених задач часто застосовують метод Гальоркіна в рамках МСЕ. У методі Гальоркіна у випадку аналізу механічної міцності виробів замість вираження потенційної енергії використають нев’язки, що виходять після заміни функції переміщення
Для практичного застосування МСЕ необхідно попередньо розробити математичні моделі скінченних елементів (СЕ) і реалізувати їх у бібліотеці СЕ програми аналізу механічної міцності. Основою математичної моделі При наявності бібліотеки СЕ застосування МСЕ зводиться до наступних операцій: 1. Створення геометричної моделі досліджуваного середовища (наприклад, деталі) за допомогою програми геометричного моделювання або шляхом зображення вручну на екрані дисплея ескізу (креслення) виробу.
2. Вибір бібліотечної моделі СЕ, завдання зовнішніх навантажень і значень геометричних і фізичних параметрів, формулювання граничних умов. Наступні операції виконуються програмою моделювання. 3. Реалізація в моделі сітки скінченних елементів. Тим самим стають відомими координати вузлових точок у моделі. 4. Приведення наявних об’ємних сил і поверхневих навантажень до вузлових точок моделі. 5. Об’єднання моделей СЕ в загальну скінченноелементну модель деталі (3.30), у якій матриця твердості 6. Зміст інших операцій відповідає блокам програми, розглянутої стосовно до аналізу на макрорівні. Оскільки аналіз механічної міцності найчастіше проводиться в стаціонарних режимах у межах пружних деформацій, те наступною операцією є рішення системи (3.30). 7. Подання результатів рішення в зручній для користувача формі. Поряд із числовим висновком результатів звичайно використається графічне зображення деформованої деталі, можливе подання розподілів напруг, деформацій, температур і т.п. усередині деталі із вказівкою їхньої інтенсивності за допомогою колірного розфарбування. До числа відомих програм аналізу по МСЕ відносяться ANSYS, NASTRAN, PATRAN і ін.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.72 (0.009 с.) |

 визначається як різниця енергії
визначається як різниця енергії  деформації тіла й роботи
деформації тіла й роботи  масових і прикладених поверхневих сил.
масових і прикладених поверхневих сил.
 — вектор-рядок відносних деформацій,
— вектор-рядок відносних деформацій,  — вектор-стовпець напруг,
— вектор-стовпець напруг, 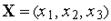 ,
,  — розглянута область у просторі
— розглянута область у просторі  . Кожний елемент
. Кожний елемент  вектора
вектора  характеризує напругу, спрямовану уздовж осі
характеризує напругу, спрямовану уздовж осі  й прикладену до площадці, перпендикулярній
й прикладену до площадці, перпендикулярній  осі. Аналогічний зміст мають індекси усіх елементів вектора
осі. Аналогічний зміст мають індекси усіх елементів вектора  .
. можна виразити через переміщення за допомогою рівнянь Коші
можна виразити через переміщення за допомогою рівнянь Коші
 — переміщення уздовж осі
— переміщення уздовж осі 
 — очевидний з (3.26) оператор диференціювання.
— очевидний з (3.26) оператор диференціювання. , що характеризує пружні властивості середовища, і представлена в Табл. 3:
, що характеризує пружні властивості середовища, і представлена в Табл. 3:
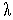 і модуль зсуву
і модуль зсуву  називають постійними Ламе. Ці коефіцієнти пов’язані з модулем пружності
називають постійними Ламе. Ці коефіцієнти пов’язані з модулем пружності  й коефіцієнтом Пуассона
й коефіцієнтом Пуассона  співвідношеннями
співвідношеннями  й
й  ;
; .
.


 . Відповідно до МСЕ це рішення апроксимується за допомогою координатних функцій і невизначених коефіцієнтів, які стосовно до сукупності скінченних елементів представимо в матричній формі:
. Відповідно до МСЕ це рішення апроксимується за допомогою координатних функцій і невизначених коефіцієнтів, які стосовно до сукупності скінченних елементів представимо в матричній формі:
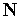 — матриця координатних функцій,
— матриця координатних функцій,  — вектор невизначених коефіцієнтів.
— вектор невизначених коефіцієнтів.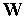 (
( (
(
 — матриця жорсткості.
— матриця жорсткості.

 — вектор навантажень. Таким чином, задача аналізу міцності, згідно МСЕ, зведена до рішення системи лінійних алгебраїчних рівнянь (3.30).
— вектор навантажень. Таким чином, задача аналізу міцності, згідно МСЕ, зведена до рішення системи лінійних алгебраїчних рівнянь (3.30). апроксимуючим вираженням
апроксимуючим вираженням  у вихідному диференціальному рівнянні Ламе (для статичного режиму)
у вихідному диференціальному рівнянні Ламе (для статичного режиму)
 — диференціальний оператор
— диференціальний оператор  , що застосовується до всіх елементів вектора
, що застосовується до всіх елементів вектора  — вектор масових і прикладених сил, віднесених до скінченного елемента. Нев’язка по області
— вектор масових і прикладених сил, віднесених до скінченного елемента. Нев’язка по області 

 -го СЕ є квадратна матриця жорсткості
-го СЕ є квадратна матриця жорсткості  скінченного елемента, розмір якої дорівнює числу
скінченного елемента, розмір якої дорівнює числу  невизначених коефіцієнтів у частині вектора
невизначених коефіцієнтів у частині вектора  простору й числа
простору й числа  вузлів, виділених у моделі
вузлів, виділених у моделі  в напрямку осі
в напрямку осі  -м вузлі. При одержанні моделі СЕ використовується матриця координатних функцій
-м вузлі. При одержанні моделі СЕ використовується матриця координатних функцій  скінченного елемента, у якої число рядків дорівнює
скінченного елемента, у якої число рядків дорівнює  й за допомогою інтегрування по просторових координатах визначають матрицю жорсткості СЕ.
й за допомогою інтегрування по просторових координатах визначають матрицю жорсткості СЕ. має порядок, рівний
має порядок, рівний  , де
, де  — загальне число вузлів. При об’єднанні елементи матриці
— загальне число вузлів. При об’єднанні елементи матриці 


